什么是RSA算法？

1976年以前，所有的加密方法都是同一种模式：

• 甲方选择某一种加密规则，对信息进行加密；

• 乙方使用同一种规则，对信息进行解密。

由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"

这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

如果能在加密信息的途中，让加密密钥与解密密钥不同，就可以很好的克服对称加密算法的弱点，这种加密模式被称为“非对称加密算法”即

甲要传密信给乙，乙先根据某种算法得出本次与甲通信的公钥与私钥；
乙将公钥传给甲（公钥可以让任何人知道，即使泄露也没有任何关系）；
甲使用乙传给的公钥加密要发送的信息原文，发送给乙密文c；
乙使用自己的私钥解密密文c，得到信息原文m.

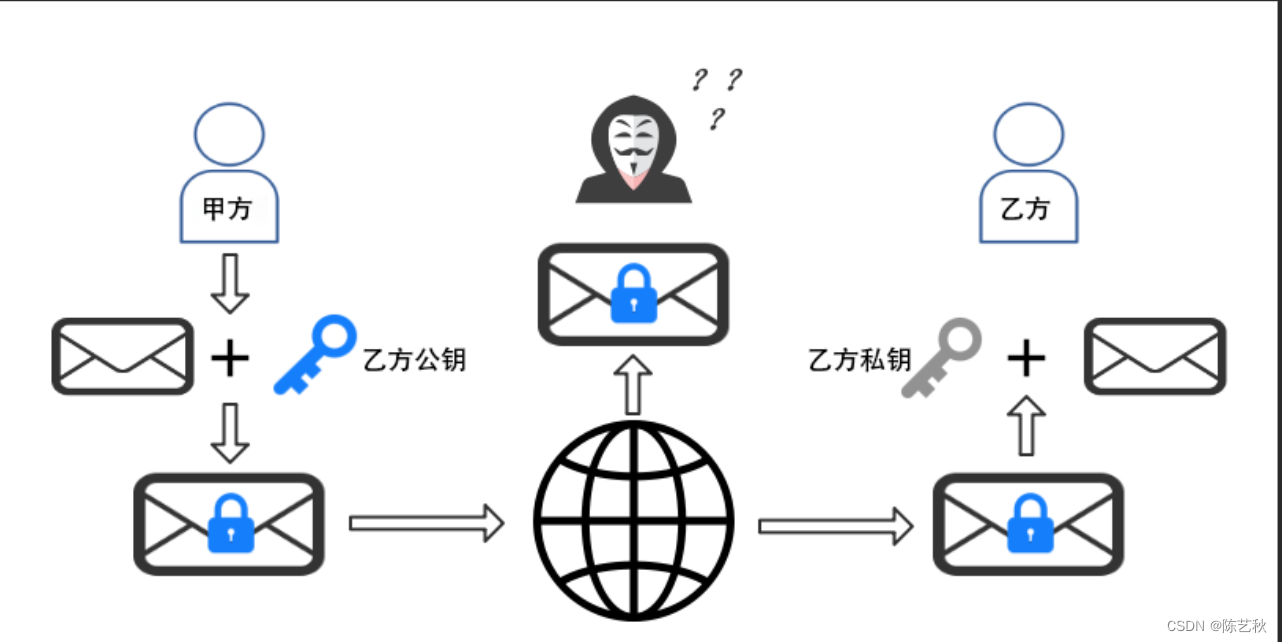
非对称加密算法，从始至终，私钥一直都在信息接收方乙处

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的

1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）三位一起实现“非对称加密算法”。就是他们三人姓氏开头字母拼在一起组成的 RSA算法

RSA算法非常可靠，密钥越长，它就越难破解，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全

RSA数论知识

质数与互质

质数（素数）是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数，否则称为合数。

如7 除了= 1 * 7 以外不能表示为其它任何两个整数的乘积，所以是一个质数

15 = 1 * 15 = 3 * 5 所以15不是一个质数而是合数

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系可以得到以下结论

• 任意两个质数构成互质数（如3与11、7与19）；

• 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57；

• 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10、5与26；

• 1和任何一个自然数在一起都是互质数,比如1和99。；

• 相邻的两个自然数是互质数

• p是大于1的整数，则p和p-1构成互质关系，比如57和56。；

• 相邻的两个奇数是互质数（如49与51）。

• p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

同余

“≡”是数论中表示同余的符号（mod就是取余的意思，一下用%代替）

定义：

给定一个正整数m， 如果两个整数a和b满足a-b能被m整除，即(a - b) % m = 0，
那么就称整数a与b对模m同余，记作a ≡ b( mod m)，同时可成立a % m = b
再次提醒注意，同余与模运算是不同的
a ≡ b( % m)仅可推出b = a % m

欧拉函数

如果任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？

求这个值的方法就欧拉函数，即φ(n)，表示的是小于等于 n 的正整数中，和 n 互质的数的个数。

例如：φ(7)中与7是互质关系的有1，2,3,4,5,6所以φ(7) = 6

欧拉函数φ(n)求值有以下几种情况：

1. 如果n = 1，则φ(n) = 1 ，因为1对任何数（包括本身）都是互质关系

2. 如果n是质数，则 φ(n) = n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

3. 如果n可以分解成两个互质的整数之积，即n = p × q，则有：φ(n) = φ(pq) = φ(p) φ(q);

1. 根据“如果两个数之中，较大的那个数是质数，则两者构成互质关系”和求值第2点可以知道：

一个数如果是质数，则小于它的所有正整数与它都是互质数；
所以如果一个数p是质数，则有： φ(p) = p-1
若我们知道一个数n可以分解为两个互质数p和q的乘积，则有
φ(n) = (p-1) (q-1)

欧拉定理和模反函数

欧拉函数的用处，在于欧拉定理

“欧拉定理”指的是如果两个正整数a和n互质，则n的欧拉函数φ(n)可以让下面的等式成立：

a^φ(n) ≡ 1( mod n) 等同于 a^φ(n) % n = 1

也就是说a的φ(n)次方向n取余的余数为1

模反元素的推导过程如下：

根据欧拉定理，有：

a^φ(n) = a × a^φ(n)−1 ≡ 1 (mod n)

令b = a^φ(n)-1，得：

ab ≡ 1(mod n) 也就是 ab % n = 1

b就是a的模反元素

如果两个正整数a和n互质，那么一定可以找到整数b

使得ab-1被n整除，或者说ab被n除的余数是1

也就是说

ab - 1 % n = 0 ab - 1 = kn

总结

以上就是RSA算法的前置知识，是我从大佬们的文章学习得来的，其实引用了许多原话，理解下来后RSA算法也不是很难，只是需要更多的练习，熟悉

RSA算法实例

假如说甲要发送一串密文cxk给乙

1. 首先我们确定两个不相等的质数p和q

实际运用中质数越大越难破解（乙选择了67和31）

2. 计算p和q的乘积n

n = 67 * 31 = 2077
n的长度就是密钥的长度，将2077写成二进制= 1000 0001 1101，一共有12位，所以这个密钥就是12位，实际应用中RSA密钥越长越难破解，一般是1024或者2048位

3. 计算n的欧拉函数φ(n)

根据公式 φ(n) = (p-1) (q-1)
φ(2077) = (67-1) (31-1) = 1980

4. 随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

乙在2到1980的整数里选择了选择了7

因为1980与7不是倍数关系，并且7是一个质数，满足条件

5. 计算e对于φ(n)的模反元素d。

所谓"模反元素"就是指有一个整数d，可以使得ed向φ(n)取余的余数为1或者说ed - 1能够被φ(n)整除

ed ≡ 1 (mod φ(n))
这个式子等价于（k为任意正整数）
ed - 1 = kφ(n)
ed - kφ(n) = 1
已知e= 7 φ(n) = 1980 带入数据得
7d - 1980k = 1接下来就是求这个二元一次方程组的结果
最后求得
（d，k） =（ 283， 1）

d = kφ(n) + 1 / e

欧几里得算法

6. 然后将n和e封装成公钥，n和d封装成私钥

n = 2077 e = 7 d = 233
公钥：
（2077，7）
私钥：
（2077，283）

7. 将公钥发送给甲

甲根据以下公式及公钥对原文xk（下面用m代替）加密成密文c

因为如果直接使用字符转十进制形式太大了，所以采用26个字母顺序分别代表密文字符

m^e ≡ c(mod n)

m^e % n = c

代入得

x = 11^7 % 2077 = 19487171 % 2077 = 757

k = 24^7 & 2077 = 4,586,471,424 % 2077 = 561

解密：

x = 757 ^283 % 2077 = 11

k = 561^283 % 2077 = 24

密钥组成与加解密公式

参考文献

RSA算法基础详解 - 黄映焜 - 博客园 (cnblogs.com)

https://www.bilibili.com/video/BV14y4y1272w/?spm_id_from=333.337.search-card.all.click&vd_source=57570933f1fff4afb052f1b8a0d1ed9e