一、931. 下降路径最小和

1.题目简介

931. 下降路径最小和
题目描述：
给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和。
下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
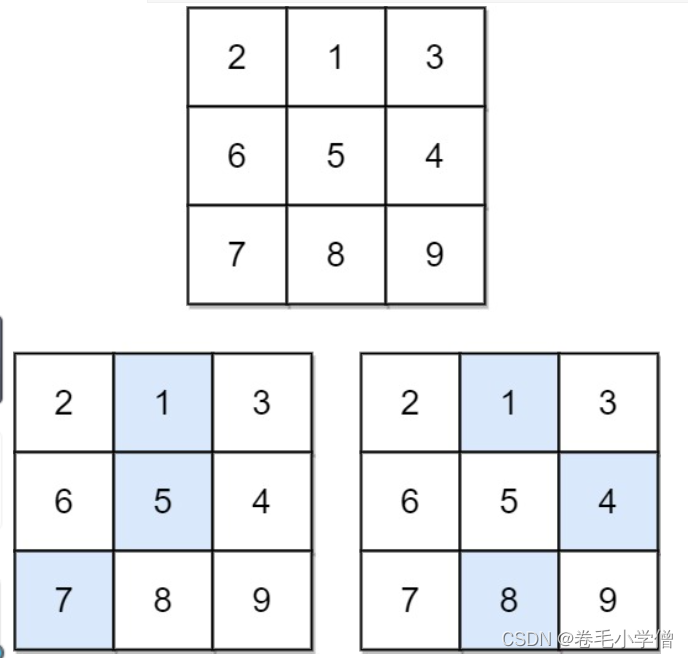
在这里插入图片描述

2.解题思路

这道题要求下降路径的最小和，即从第一行到最后一行的所有路径的最小和。
根据动态规划的五步解题思路：
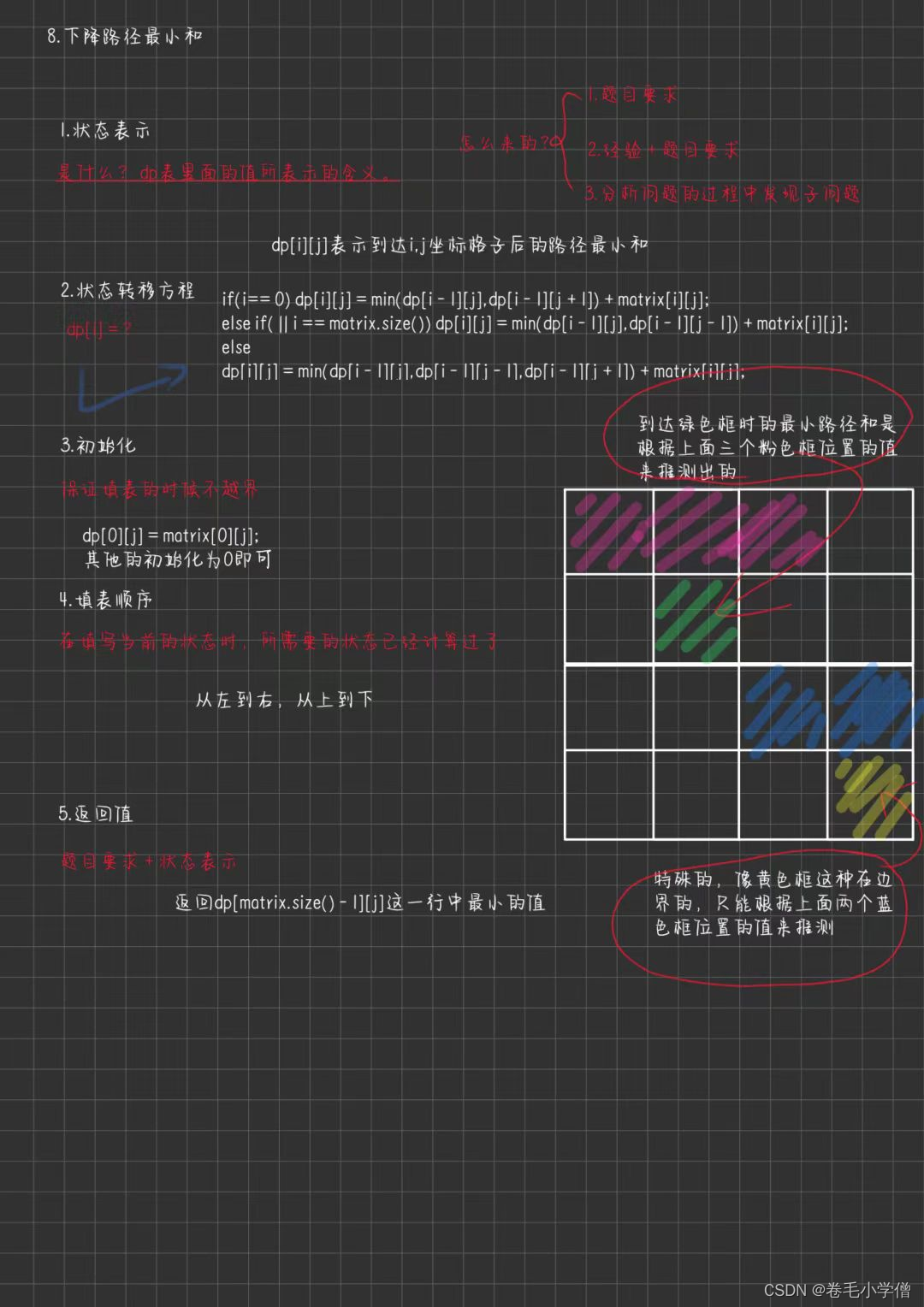
在这里插入图片描述

3.代码

具体代码如下（C++）：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        vector<int> v(matrix[0].size(), 0);
        vector<vector<int>> dp(matrix.size(), v);
        for(int j = 0;j < matrix[0].size(); ++j)
        {
            dp[0][j] = matrix[0][j];
        }
        for(int i = 1;i < matrix.size(); ++i)
        {
            for(int j = 0;j < matrix[0].size(); ++j)
            {
                if(j == 0)
                {
                    dp[i][j] = min(dp[i - 1][j], dp[i - 1][j + 1]) + matrix[i][j];
                }
                else if(j == (matrix[0].size() - 1))
                {
                    dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1]) + matrix[i][j];
                }
                else
                {
                    dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]), dp[i - 1][j + 1]) + matrix[i][j];
                }
            }
        }
        int ret = INT_MAX;
        for(int j = 0;j < matrix[0].size(); ++j)
        {
            ret = min(ret, dp[matrix.size() - 1][j]);
            cout<<j<<":"<<dp[matrix.size() - 1][j]<<endl;
        }
        return ret;
    }
};

4.运行结果

在这里插入图片描述

二、64. 最小路径和

1.题目简介

64. 最小路径和
题目描述：
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
在这里插入图片描述

2.解题思路

这道题要求最小路径和，可以化简为求从左上角到路径中某个格子的最小路径和，然后再计算从左下角到右下角的最小路径和。
根据动态规划的五步解题思路：
在这里插入图片描述

3.代码

具体代码如下（C++）：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        vector<int> v(grid[0].size(), 0);
        vector<vector<int>> dp(grid.size(), v);
        dp[0][0] = grid[0][0];
        for(int j = 1;j < grid[0].size(); ++j)
        {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for(int i = 1;i < grid.size(); ++i)
        {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for(int i = 1;i < grid.size(); ++i)
        {
            for(int j = 1;j < grid[0].size(); ++j)
            {
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[grid.size() - 1][grid[0].size() - 1];
    }
};

4.运行结果

在这里插入图片描述

三、面试题 17.16. 按摩师

1.题目简介

题目描述：
面试题 17.16. 按摩师
一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。
在这里插入图片描述

2.解题思路

这道题要求按摩师最大工作分钟数，可以计算每一个预约中按摩师接不接该预约的最大分钟数，然后最终计算所有的预约最大分钟数（根据具体情况，有时候不接当前预约反而可以获得更大的工作时间）
根据动态规划的五步解题思路：
在这里插入图片描述

3.代码

具体代码如下（C++）：

class Solution {
public:
    int massage(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        vector<int> v(2, 0);
        vector<vector<int>> dp(nums.size(), v);
        dp[0][0] = 0;
        dp[0][1] = nums[0];
        for(int i = 1;i < nums.size(); ++i)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
            dp[i][1] = dp[i - 1][0] + nums[i];
        }
        return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
    }
};