一、进制转换

1.1 二进制转十六进制

因 $2^4=16$，所以每4个二进制位，可表示为1个十六进制。例如如下：

• 00001111(B) = F(H)、0xF、0x0F
• 11111111(B) = FF(H)、0xFF
• 111100001111(B) = F0F(H)、0xF0F
• 1111111100001111(B) = FF0F(H)、0xFF0F

1.2 十六进制转二进制

每1个十六进制 转换为 4个二进制位即可。例如如下：

• 0xF0F = 111100001111(B) = 0000111100001111(B)
• 0xFF0F = 1111111100001111(B)

二、进制相减

2.1 十六进制

例如：0xA000 - 0x0800

• 先从末尾开始减：最后两位的0x0000-0x0000 = 0x0000
• 再倒数第三位相减 0x0000 - 0x0800，因为不够减，所以借位得到16（因为是十六进制相减），即 16 - 8 = 8
• 在倒数第四位相减 0xA000 - 0x0000，因为已经被借走了一位，则变为 0x9000 - 0x0000 = 0x9000
  故最终答案为 0x9800

PS：类比二进制相减即容易理解了

三、内存地址偏移计算

例如：若一栋楼共100层，最底为第0层，则最顶为第99层。因为从0到(n-1)共有n个数，如下图：

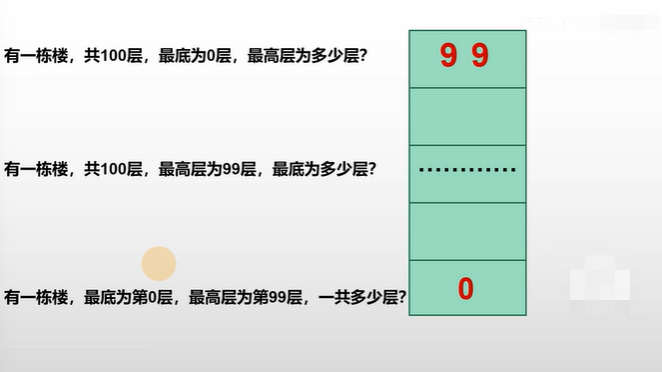
3.1 根据首末地址，求存储容量

题目 如下：

如下图所示，首地址是 30000H，末地址是 AFFFFH。

因为题目说明内存以字节编制，则说明即每个地址是一个字节（即楼房的每层放了1个byte，即8个bit）。

题意问存储容量，即问能存储多少 bit。

---

题解如下：

• 先求楼层数：

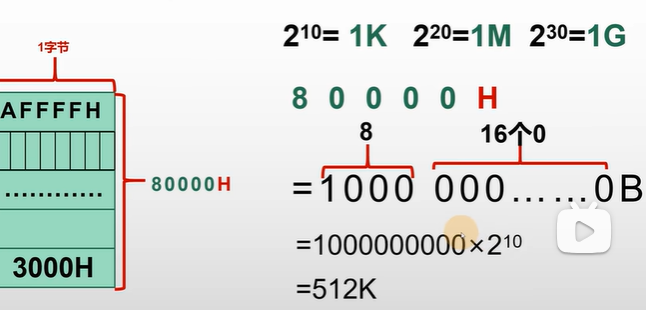
  • AFFFF(H) - 30000(H) + 1 = 7FFFF(H) + 1 = 80000(H)
  • 而 80000(H) = 1000-0000-0000-0000-0000(B) = 2^19，即 2 ^ 19 Bytes
    
  • 而 $2^{1}0=1K$、$2^{2}0=1M$、$2^{3}0=1G$
  • 故 2 ^ 19 bytes = $2^9$ * $2^{10}$ = $2^{9}Kbytes$ = $2^{9}KB$ = 512 KB
    

• 故最终答案为能存储 512 KB 的容量（如下图）：

3.2 根据末地址 和 存储容量，求首地址

题目如下：

---

题解如下：

若题目未指明，则默认每个地址为 1个字节。

因为共 2KB 即 2K Bytes 即 2048 Bytes，需将 2000（十进制）转换为 十六进制。

因常识为 1024 = $2^{10}$，故 2000 = $2^{11}$ = 2后面1个0(B) = 1000-0000-0000(B) = 800(H) 即 0x800。详见下图：

而因公式为 $存储空间=末地址-首地址+1$，故 $首地址=末地址-存储空间+1$ = 9FFF(H) - 0800(H) + 1(B)= A000(H) - 0800(H) = 9800(H)。详见下图：