leetcode354. 俄罗斯套娃信封问题

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/russian-doll-envelopes

题目描述:

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。
注意：不允许旋转信封。

示例 1：
输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例 2：
输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1

提示：
1 <= envelopes.length <= 105
envelopes[i].length == 2
1 <= wi, hi <= 105

解题思路

合法嵌套,是大的套小的,因此这个题就是最长递增子序列的一个变种.当于在二维平面中找一个最长递增的子序列，其长度就是最多能嵌套的信封个数。
递增子序列的解题方法可以查看leetcode300. 最长递增子序列
如何在二维数组中,运用递增子序列的方式.我们就需要现堆这个二维数组处理一下了:
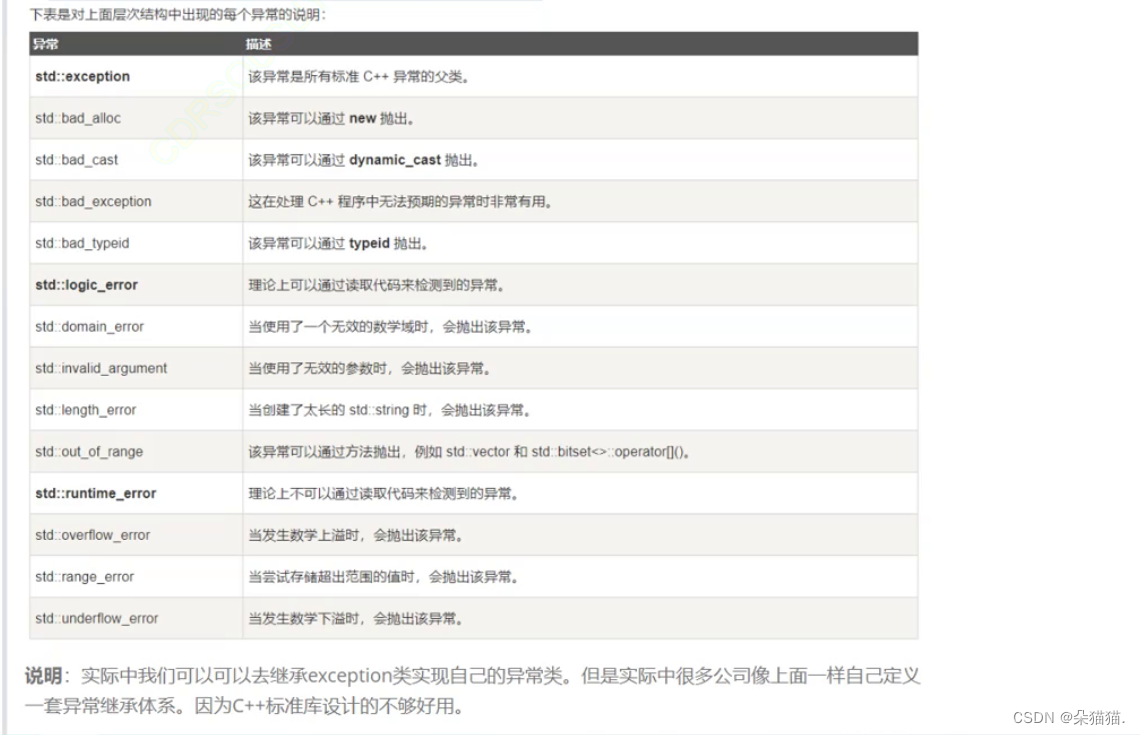
先对宽度 w 进行升序排序，如果遇到 w 相同的情况，则按照高度 h 降序排序；之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。
用图演示一下,就明白为何能这样做了:

然后在 h 上寻找最长递增子序列，这个子序列就是最优的嵌套方案：

代码演示

   public int maxEnvelopes(int[][] envelopes) {
        int N = envelopes.length;  
         Arrays.sort(envelopes, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0];
            }
        });

        int[]heights = new int[N];  
        for(int i = 0; i < N; i++){
            heights[i] = envelopes[i][1];    
        }
        return lengthOfLIS(heights);
    }
		
   	/**
   	* 最长递增子序列 可以直接复制进力扣测试
   	*/
    int lengthOfLIS(int[] nums) {
       int N = nums.length;
       //动态规划表
       int[]dp = new int[N];
       for(int i = 0; i < N; i++){
       	//base case 每个位置本身长度
           dp[i] = 1;
           for(int j = 0;j < i; j++){
            // i 位置依次向前比 ,比j 位置大,就是 1 + dp[i]
           // 根据不同j位置上的数,来更新最大值
               if(nums[i] > nums[j]){
                  dp[i] = Math.max(dp[i],1 + dp[j]);  
               }
               
           }
       }
       int res = 0;
         //取出 dp表中的最大值 就是我们要的答案.
       for (int i = 0; i < dp.length;i++){
           res = Math.max(res,dp[i]);
       }
       return res;
    }

上面的lengthOfLIS 这个方法时间复杂度是O(N2) n平方的,时间限制上可能过不去,可以进行下面的二分法改造>

 int lengthOfLIS(int[] nums) {
         int N = nums.length;
         int[]ends = new int[N];
         int count = 0;
         for(int i = 0; i < N ; i++){
            int cur = nums[i];
            int L = 0;
            int R = count;
            while(L < R){
                int mid = (L + R) / 2;
                if(ends[mid] >= cur){
                    R = mid;
                }else{
                    L = mid + 1;
                }
            }
            //
            if(L == count){
                count++;
            }
            ends[L] = cur;
         }
         return count;
     }