今天正好有点时间就想着把之前零星时间里面做的一点小东西整合一下梳理出来，本文的核心目的就是想要基于python来开发实现各种有趣的数学曲线的可视化展示。

笛卡尔心形线

笛卡尔心形线是一种二维平面曲线，由法国数学家笛卡尔在17世纪提出。它得名于其形状类似于传统的心形符号 ❤️。

笛卡尔心形线的方程可以表示为：

(x^2 + y^2 - 1)^3 - x^2 * y^3 = 0

其中，(x, y) 是心形线上的点坐标。这个方程使用了平方和立方项，使得曲线具有两个对称的凸起，并相互连接形成心形的外观。

这条曲线是一个典型的代数曲线，具有对称性和美学吸引力，因此经常用于表达爱、浪漫和情感的概念。它在数学绘图、图像处理、计算机图形学和艺术领域中经常被使用。

基于python的代码实现也是很简单的如下所示：

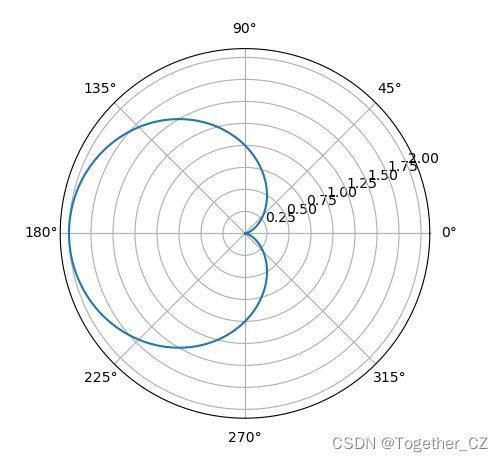
a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = a*(1 - np.cos(theta))
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

结果如下所示：

 玫瑰曲线

玫瑰曲线（Rose Curve），也称为罗塞特曲线（Roser Curves）或罗赛花曲线，是一类具有美丽花朵形状的极坐标曲线。它的方程通常由下式给出：

r = a * cos(nθ) 或 r = a * sin(nθ)

其中，r 和 θ 是极坐标系中的半径和角度，a 是常数，n 是指示螺旋节数的整数。

当 n 为奇数时，玫瑰曲线会产生具有 n 个花瓣的形状，而当 n 为偶数时，则会产生双倍数量的花瓣。参数 a 控制着曲线的大小。

玫瑰曲线在几何学和数学可视化中广泛使用，并因其优雅的外观而成为艺术、设计和装饰中的常见图案。通过改变参数 a 和 n 的值，可以得到不同形状和花瓣数量的玫瑰曲线。

以下是一个 Python 示例代码，用于绘制玫瑰曲线：

a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = a* np.sin(10*theta)
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

结果如下所示：

 阿基米德曲线

阿基米德曲线（Archimedean Spiral），也称为等距螺线，是一种由古希腊数学家阿基米德在公元前3世纪发现的曲线。它以阿基米德的名字命名，因为他对其性质和特点做出了研究。

阿基米德曲线的参数方程可以表示为：

x = r * cos(theta) y = r * sin(theta)

其中，(x, y) 是平面上的点坐标，r 是距离原点的半径，theta 是与 x 轴的夹角。

阿基米德曲线的特点是以恒定的速率延伸出去，并且每个圈的弧长相等

基于Python的代码实现如下所示：

a = 1
theta = np.linspace(0, 10*np.pi, 1000)
r = a * theta
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

结果如下所示：

 伯努利双纽线

伯努利双纽线（Bernoulli lemniscate），也称为伯努利曲线或双纽线曲线，是数学中的一个重要曲线。它由瑞士数学家雅各布·伯努利（Jacob Bernoulli）在1694年研究椭圆催化器问题时引入，并命名为"lemniscus"，意为"ribbon"（带子）。伯努利双纽线的方程可以表示为：

(x^2 + y^2)^2 = a^2 * (x^2 - y^2)

其中，a是一个常数，决定了曲线的形状和大小。伯努利双纽线是一个对称的闭合曲线，形状类似于一个蝴蝶的翅膀，两个“纽”字形状的回路从原点开始并相交于 (0, 0)。

伯努利双纽线在数学与物理学领域中有许多应用，尤其在微积分、复变函数论和流体力学等领域经常出现。它还被广泛用于图形设计和艺术表达中，因其独特的外观而备受欣赏。

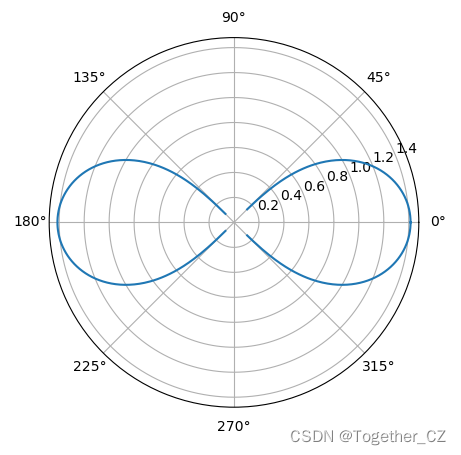
a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = np.sqrt(2*(a**2)*np.cos(2*theta))
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

结果如下所示：

 二项分布

二项分布曲线（Binomial distribution curve）是描述二项分布的概率分布曲线。二项分布是离散型概率分布，用于描述在一系列独立的、相同的随机试验中成功次数的概率分布情况。

二项分布曲线以两个参数来描述：试验的次数（n）和每次试验成功的概率（p）。它的概率质量函数可以表示为：

P(X = k) = C(n, k) * p^k * (1 - p)^(n-k)

其中，X 是成功次数，k 是取值范围内的一个特定值，C(n, k) 是组合数，等于 n! / (k!(n-k)!)，p 是每次试验成功的概率，(1 - p) 是每次试验失败的概率。

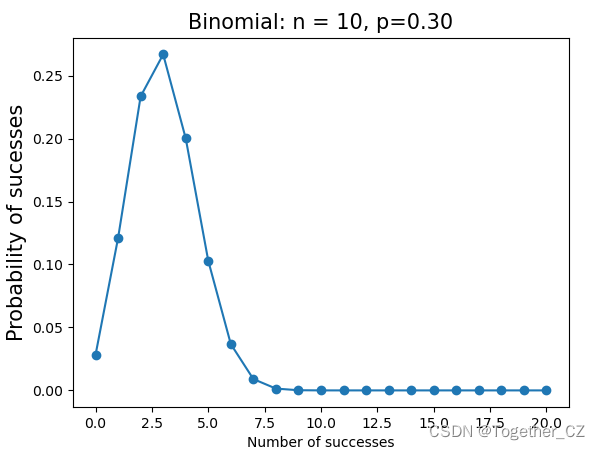
二项分布曲线通常呈现出对称的钟形，其峰值出现在成功次数的期望值附近。随着试验次数增加，二项分布趋向于正态分布，这是由于中心极限定理的效应。

二项分布曲线在统计学和概率论中具有广泛的应用，特别是在重复进行二元决策或随机事件的实验中，例如硬币投掷、品质控制和调查研究等方面。该曲线可以帮助我们推断在给定概率下出现特定结果的可能性，并提供统计推断和决策依据。

mean,var,skew,kurt=binom.stats(n,p,moments='mvsk')
print(mean,var,skew,kurt)
#ppf:累积分布函数的反函数。q=0.01时，ppf就是p(X<x)=0.01时的x值。
x=np.arange(binom.ppf(0.01,n,p),binom.ppf(0.99,n,p))
ax.plot(x,binom.pmf(x,n,p),'o')
plt.rcParams['font.sans-serif']=['SimHei']
plt.title(u'二项分布概率质量函数')
plt.show()

结果图像如下所示：

 星形线

星形线（Astroid）是一种数学曲线，也被称为星形四叶草。它的名称来自于其形状类似于一个具有尖角和凹面的星星。

星形线的参数方程可以表示为：

x = a * cos^3(t) y = a * sin^3(t)

其中，t 是参数，a 是控制曲线大小的常数。

星形线具有对称性，且在原点处交汇。它们的形状紧凑且具有锐利的角度，这使得它们在几何学、数学和物理学等领域中具有一定的重要性。星形线经常出现在曲线绘图、图形设计和计算机生成图像等应用中，因为其美观而有吸引力的外观。

代码实现如下所示：

delta = 2/(2*num)
points1=np.zeros((2*(2*num+1),2),dtype=np.float64)
points=np.zeros(((2*num+1),2),dtype=np.float64)
for i in range(2*num+1):
    points[i,0] = -1.0+delta*i
    #points[i+2*num+1,0] = -1+delta*i
    points[i,1] = (1-(np.abs(-1+delta*i))**ntype)**(1./ntype)
    #points[i+2*num+1,1] = -(1-(np.abs(-1+delta*i))**ntype)**(1./ntype)
points1[:2*num+1,0]=points[:,0]
points1[2*num+1:,0] =points[:,0]
x=points[:,0]
y=points[:,1]
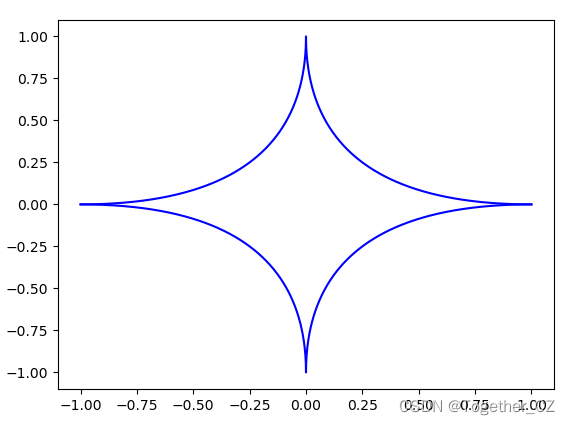
plt.clf()
plt.plot(x,y,color='b')
plt.plot(x,-1*y,color='b')
plt.show()

结果如下所示：

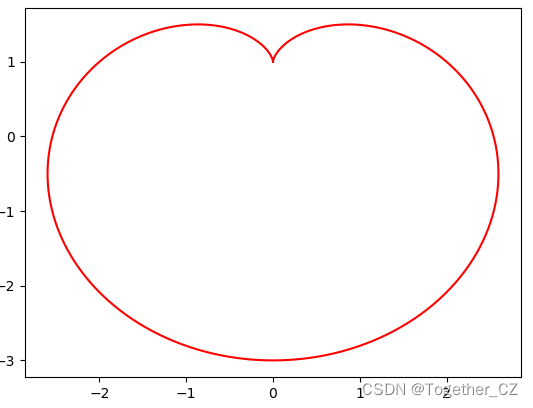
 心形曲线

心形曲线（Heart curve）是一种浪漫景象中常见的数学曲线，其轮廓形状类似于一个风格化的心形。它有多种方式可以表示，以下是其中一种常见的参数方程：

x = 16 * sin^3(t) y = 13 * cos(t) - 5 * cos(2t) - 2 * cos(3t) - cos(4t)

其中，t 是参数，x 和 y 分别表示心形曲线上点的横纵坐标。

心形曲线通常被视为爱、情感和浪漫的象征，因此在各种庆祝活动、情人节或表达爱意的场合中经常出现。它也在数学、图形设计和艺术创作中广泛应用，并成为人们传达深情意味和感情表达的图形符号之一。

python代码实现如下所示：

t = np.linspace(0 , 2 * np.pi, 1024)
X = a*(2*np.cos(t)-np.cos(2*t))
Y = a*(2*np.sin(t)-np.sin(2*t))
plt.plot(Y, X,color='r')
plt.show()

结果如下所示：