every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
说明: 后续增补
1. 正文
1.1 整体理解
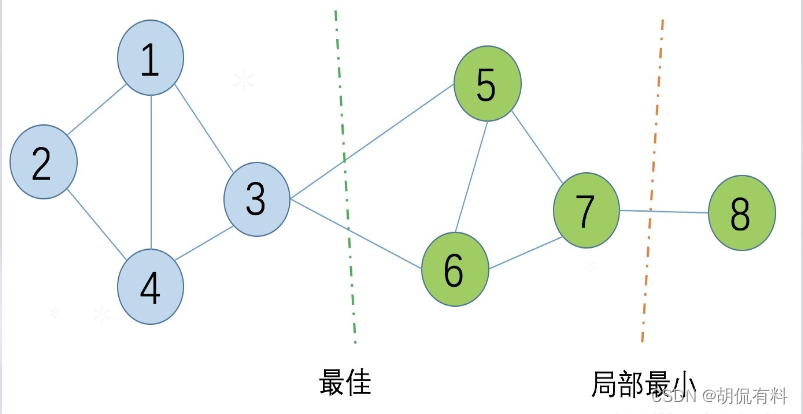
谱聚类(Spectral Clustering)是一种基于图论的聚类方法,将带权无向图划分为两个或两个以上的最优子图。使子图内尽量相似,子图间距离尽量较远。其中的最优是指最优目标函数不同。有以下两种:
- smallest cut
- best cut
如下图所示:
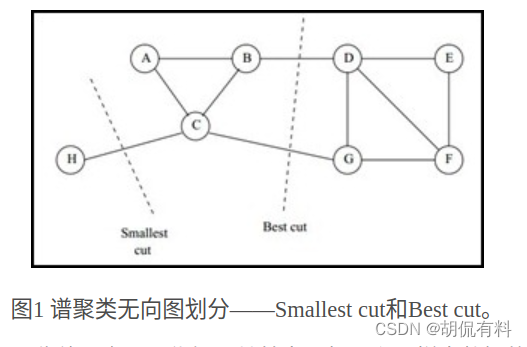
1.1.1 无向图
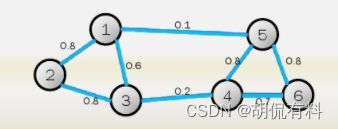
如下图所示,由若干顶点和边组成,由于边没有方向,故称为无向图。其中,
点集合:
V
=
{
v
1
,
v
2
,
.
.
.
.
.
,
v
3
}
V = \{v1,v2,.....,v3\}
V={v1,v2,.....,v3}
边集合:
E
=
{
e
1
,
e
2
,
.
.
.
.
.
,
e
3
}
E = \{e1,e2,.....,e3\}
E={e1,e2,.....,e3}
所以,图表示为 G ( V , E ) G(V,E) G(V,E)
权重矩阵(邻接矩阵)
W
W
W,
W
i
j
W_{ij}
Wij表示
i
i
i和
j
j
j之间的权重,由于是无向图,所以
W
i
j
=
W
j
i
W_{ij}=W_{ji}
Wij=Wji
1.1.2 度和度矩阵
在数据结构中,度定义为与该点直接连接的顶点个数。
在这里,定义如下:
d
i
=
∑
j
=
1
n
W
i
j
d_i = \sum_{j=1}^{n}W_{ij}
di=j=1∑nWij
即,某行(或列)的权重和。
度矩阵为n个度构成的对角阵,如下:
[ d 1 0 ⋯ 0 0 d 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ d n ] \begin{bmatrix} {d_{1}}&{0}&{\cdots}&{0}\\ {0}&{d_{2}}&{\cdots}&{0}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {0}&{0}&{\cdots}&{d_{n}}\\ \end{bmatrix} d10⋮00d2⋮0⋯⋯⋱⋯00⋮dn
1.1.3 相似矩阵
注意: 我们可以计算两点间的距离,生成一个邻接矩阵表示我们点与点的关系(即,我们所说的图),这里的相似矩阵是在“距离矩阵”的基础上(根据距离的远近判断是否相似)根据一定的方法(下面的三种方法)进一步“筛选”
(可以粗略理解,有的点离的比较远不要了)
上述的权重矩阵 由任意两点之间的权重构成,在实际当中,我们并不能直接获得权重,只有数据点的定义,通常会通过两点之间的距离计算权重。距离远权重点,距离近权重高。通常由三种方法
(1). ϵ ϵ ϵ-邻近法(使用较少)
设置一个阈值 ϵ ϵ ϵ,计算两点之间的欧式距离并与阈值比较,
W
i
j
=
{
0
,
i
f
s
i
j
>
ϵ
ϵ
,
i
f
s
i
j
⩽
ϵ
W_{ij}=\left\{ \begin{matrix} 0 , & if &s_{ij}>ϵ \\ ϵ, &if &s_{ij}\leqslantϵ \end{matrix} \right.
Wij={0,ϵ,ififsij>ϵsij⩽ϵ
用阈值筛选距离,卡的比较死,样本之间权重之间和0,缺失很多信息
(2). k-近邻法
对于任意一点,求取与他最近的k个顶点,该顶点与k个顶点的权重由计算得到(都大于0,其余顶点距离为0),但会导致得到的相似矩阵不对称。如:
i
i
i在
j
j
j的
k
k
k个近邻中,但
j
j
j可能不在
i
i
i的
k
k
k个近邻中。针对这个问题由两种解决方法:
说明:
s
i
j
s_{ij}
sij表示距离
a. 方法一
宽松版
只要一个满足k近邻,则令
W
i
j
=
W
j
i
W_{ij}=W_{ji}
Wij=Wji,只有同时不满足k近邻,则为0。
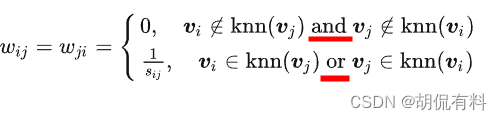
b. 方法二
严格版
两个顶点互为近邻,才计算距离,否则权重为0。
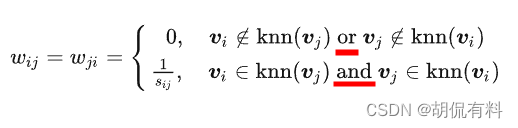
(3). 全连接
计算所有点之间的相互连接,因此权重都大于0,可以选择不同 核函数计算距离,常用的有:
- 多项式核函数
- 高斯核函数
- sigmoid核函数

1.1.4 拉普拉斯矩阵
L = D − W L = D - W L=D−W
D D D 为度矩阵, W W W为上面的邻接矩阵
1.1.5 切图,聚类
下面进入重点了,现在我们要对上面说到的无向图进行切图。
切割优化目标:
C
o
s
t
(
G
1
,
.
.
.
G
2
)
=
∑
i
C
(
G
i
,
G
i
^
)
Cost(G1,...G2) = \sum_{i}C(G_i,\hat{G_{i}})
Cost(G1,...G2)=i∑C(Gi,Gi^)
C
(
G
1
,
G
2
)
=
∑
i
∈
G
1
,
j
∈
G
2
w
i
j
C(G_1,G_2) = \sum_{i\in G_1,j\in G_2}w_{ij}
C(G1,G2)=i∈G1,j∈G2∑wij
- 目标是使切割子图时间的权重和最小,即,切割的边最少。
- 切割中可能会出现局部最优,因此,根据不同的切割方法有不同的切图方法。
(1). RatioCut切图
(2). RatioCut切图
目标: 使子图的节点数尽可能的大
R
a
t
i
o
n
C
u
t
(
G
1
,
.
.
.
G
2
)
=
∑
i
C
(
G
i
,
G
i
^
)
∣
G
i
^
∣
RationCut(G1,...G2) = \sum_i{C(G_i,\hat{G_i}) \over \mid \hat{G_i} \mid }
RationCut(G1,...G2)=i∑∣Gi^∣C(Gi,Gi^)
分母为子图的节点个数
(3). NCut切图
目标: 考虑每个子图边的权重和
N
C
u
t
(
C
1
,
.
.
.
C
k
)
=
∑
i
C
(
G
i
,
G
I
^
)
v
o
l
(
G
i
^
)
NCut(C_1,...C_k) = \sum_i{C(G_i,\hat{G_I} )\over vol(\hat{G_i})}
NCut(C1,...Ck)=i∑vol(Gi^)C(Gi,GI^)
分母为子图各边的权重和
1.2 计算流程
核心主要三部分:
- 相似矩阵的生成(常用:全连接方法)
- 切图方式(常用:NCut)
- 最后的聚类方法(常用:K-Means)