上一节的内容中,我们对于扩展卡尔曼EKF算法进行了讲解,今天我们对上一节的内容进行仿真。
话不多说,开整!!!
仿真背景
我们以一个目标的位置信息为例,其状态方程如下所示:
X
k
=
0.5
X
k
−
1
+
2.5
X
k
−
1
1
+
X
k
−
1
2
+
8
cos
(
1.2
k
)
+
V
k
(
1
)
X_k=0.5X_{k-1}+\frac{2.5X_{k-1}}{1+X^2_{k-1}}+8\cos(1.2k)+V_k \quad(1)
Xk=0.5Xk−1+1+Xk−122.5Xk−1+8cos(1.2k)+Vk(1)
其观测方程为:
Z
k
=
X
k
2
20
+
W
k
(
2
)
Z_k=\frac{X_{k}^{2}}{20}+W_k\quad(2)
Zk=20Xk2+Wk(2)
其中:
V
k
V_k
Vk和
W
k
W_k
Wk分别为过程噪声和量测噪声;
X
k
−
1
X_{k-1}
Xk−1: k-1时刻的状态值;
X
k
X_{k}
Xk: k时刻的状态值;
从上述的两个公式中,我们可以看到和之前研究的线性方程不一样,此时的状态转移不再是线性转移,因此需要使用EKF进行数据滤波。
那么状态值的预测方程和量测值的预测方程为:
X
k
,
k
−
1
=
0.5
X
k
−
1
+
2.5
X
k
−
1
1
+
X
k
−
1
2
+
8
cos
(
1.2
k
)
(
3
)
X_{k, k-1}=0.5X_{k-1}+\frac{2.5X_{k-1}}{1+X^2_{k-1}}+8\cos(1.2k) \quad(3)
Xk,k−1=0.5Xk−1+1+Xk−122.5Xk−1+8cos(1.2k)(3)
Z
k
,
k
−
1
=
X
k
∣
k
−
1
2
20
(
4
)
Z_{k,k-1}=\frac{X^2_{k|k-1}}{20} \quad(4)
Zk,k−1=20Xk∣k−12(4)
其中:
X
k
,
k
−
1
X_{k, k-1}
Xk,k−1:k-1时刻对k时刻的状态预测值;
Z
k
,
k
−
1
Z_{k, k-1}
Zk,k−1:k-1时刻对k时刻的观测预测值;
一阶线性化
根据上一节的内容,我们先对状态方程(1)线性化,得到状态转移矩阵:
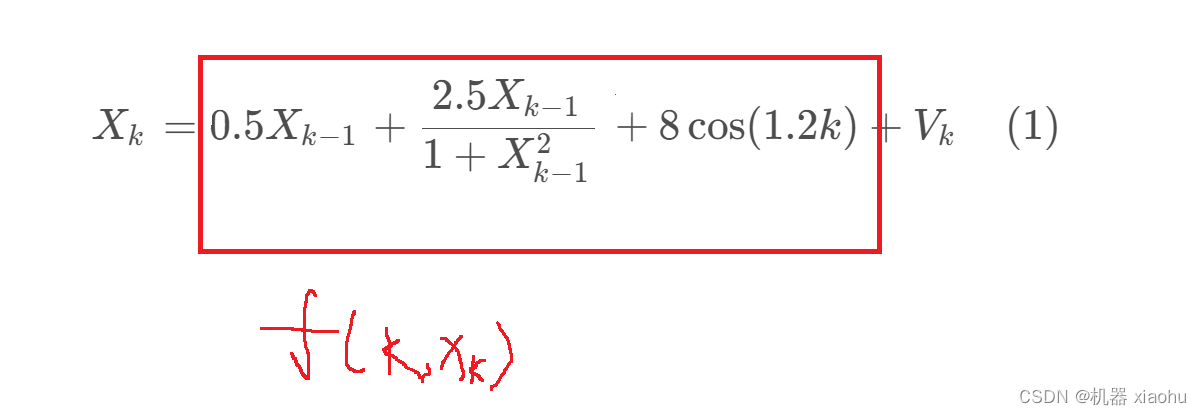
我们对
f
(
k
,
X
k
)
f(k,X_k)
f(k,Xk)关于
X
k
X_k
Xk求导,可以得到:
Φ
(
k
)
=
∂
f
∂
X
=
0.5
+
2.5
[
1
−
X
k
,
k
−
1
2
]
[
1
+
X
k
,
k
−
1
2
]
2
\Phi(k)=\frac{\partial f}{\partial X}=0.5+\frac{2.5[1-X^2_{k, k-1}]}{[1+X^2_{k, k-1}]^2}
Φ(k)=∂X∂f=0.5+[1+Xk,k−12]22.5[1−Xk,k−12]
然后对量测方程线性化,得到量测矩阵:
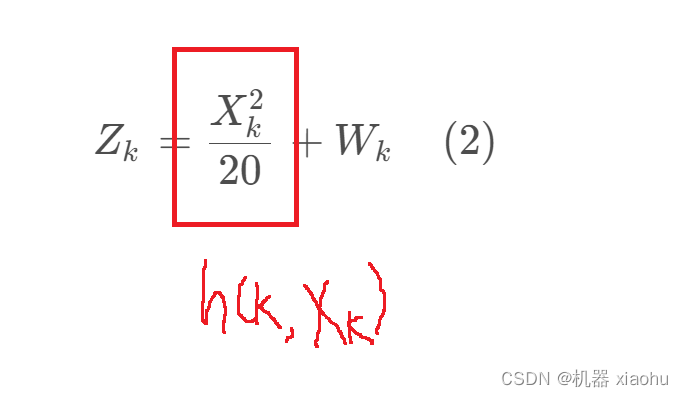
求导,得到量测矩阵
H
H
H:
H
(
k
)
=
∂
h
∂
X
=
X
k
∣
k
−
1
10
H(k)=\frac{\partial h}{\partial X}=\frac{X_{k|k-1}}{10}
H(k)=∂X∂h=10Xk∣k−1
MATLAB仿真
仿真背景
对于一维模型,进行MATLAB仿真,仿真参数设置如下:
- 处置位置X(0) = 11;
- 过程噪声方差:10;
- 量测噪声方差:1
- 仿真次数:50
仿真效果
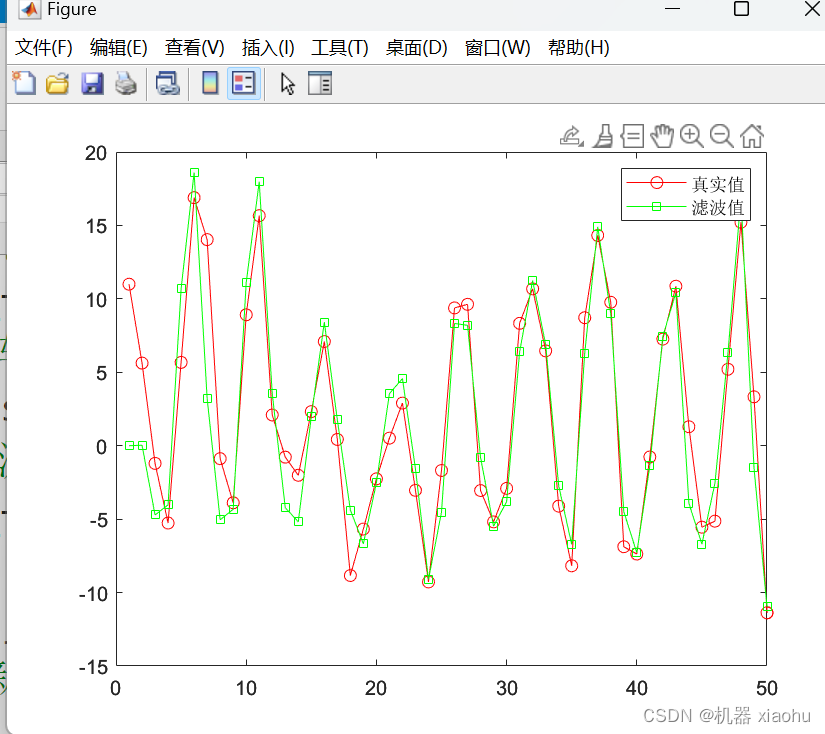
通过仿真效果可以看到,EKF对于非线性模型的滤波具有较好的滤波效果。
如果方便,辛苦大家点个赞和关注哦!
您的点赞或评论或关注是对我最大的肯定,谢谢大家!!!









![[Web前端] Servlet及应用](https://img-blog.csdnimg.cn/a32fbfcd26cb405995d8c8f936b0dd2a.png)