补一个坑 

目录

以力扣560为例：

力扣1248，优美子数组

 力扣974 和可被 K 整除的子数组

力扣523.连续的子数组和

---

浅谈一下前缀和：

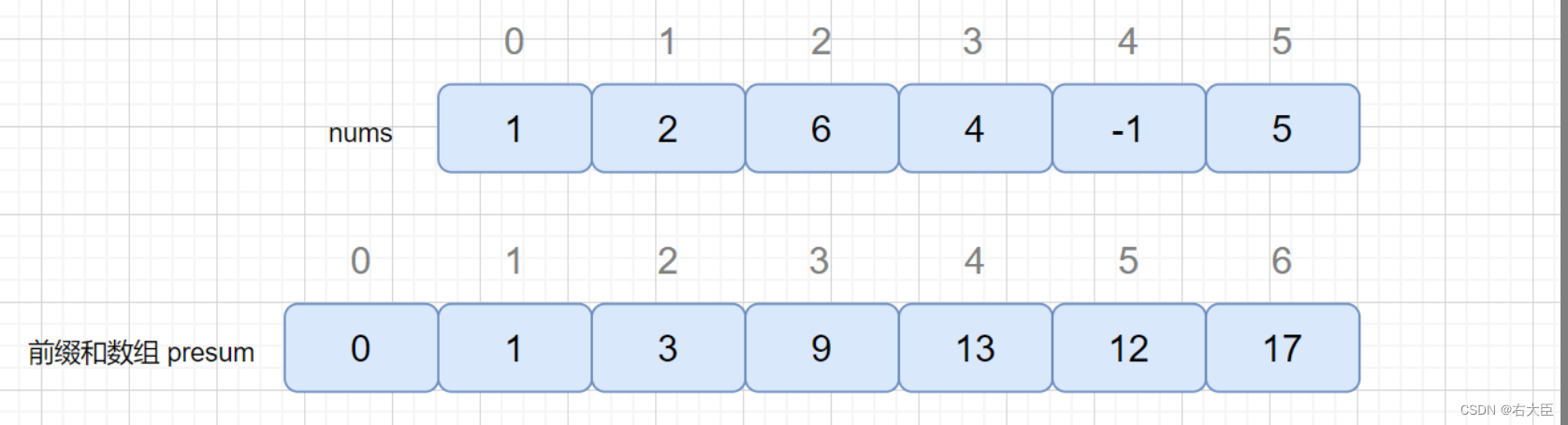
我们通过前缀和数组保存前 n 位的和，presum[1]保存的就是 nums 数组中前 1 位的和，也就是 presum[1] = nums[0], presum[2] = nums[0] + nums[1] = presum[1] + nums[1]. 依次类推，所以我们通过前缀和数组可以轻松得到每个区间的和

for(int i=0;i<nums.size();++i)
{
    presum[i+1]=presum[i]+nums[i];
}

下面说说map+前缀和

思路像极了两数之和的问题，找k存在否，我们找target-k就可以

以力扣560为例：

我们可以直接暴力ac，以前缀和加map就是，map存的是各个和以及他对应出现的次数

精华如下图：我们只要统计各个阶段前缀和出现的次数，只要有能和k组成新的前缀和的，那就说明k也是存在的，且presum-k的次数不就是k出现的次数吗，，还是两数之和的问题

至于给map初始0赋值，也是为了能让一开始找到前缀和等于k的位置能计算上，，这个初始化也是必须有的

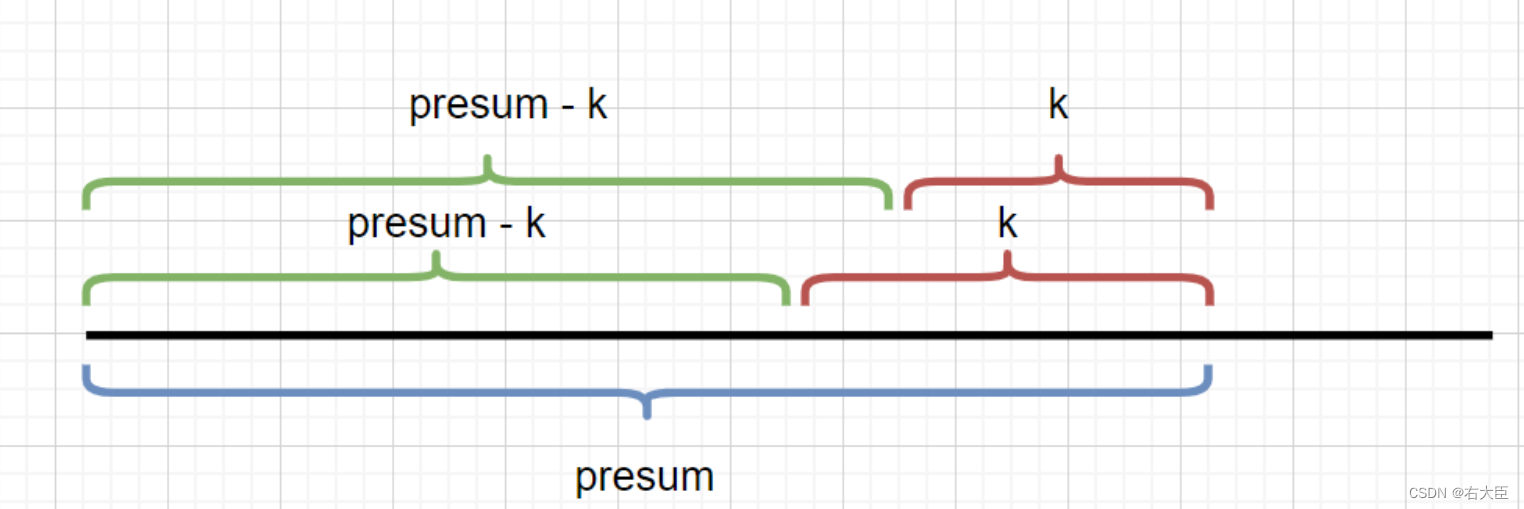
map给在初始化的时候给0一个元素，，相当于那个前缀和数组的0号下标位置给个初始值

    int subarraySum(vector<int>& nums, int k) {
        int ans=0;
        unordered_map<int,int>mp{{0,1}};
        int sum=0;
        for(int i=0;i<nums.size();++i)
        {
            sum+=nums[i];
            
            if(mp.count(sum-k)) //就说明前面的值和k能组成现在的前缀和，说明这一部分k就是存在的
            {
                ans+=mp[sum-k];//记录有多少个前面部分能和k组成现在sum，这个次数也就是这一部分k出现的次数
            }
            mp[sum]++;//相当于各个前缀和的次数
        }
        
        return ans;
    }

上面这个代码模式可以说是所有map+前缀和的模板代码了

下面给出剩下常见的map+前缀和的问题：

力扣1248，优美子数组

求子数组里面有k个奇数的，，转换一下思路。我们可以把奇数转换为1，偶数是0.。那么整个数组就是0 1组合，，那么找奇数，不就是找子数组和等于k，因为只有奇数才是有值的，偶数0不起作用啊,,转换成这样了 

套用上面模板，如下ac：

    int numberOfSubarrays(vector<int>& nums, int k) {
        unordered_map<int,int>mp{{0,1}};
        int ans=0;
        int sum=0;

        for(int i=0;i<nums.size();++i)
        {
            sum+=nums[i]%2; //相当于奇数变1，偶数变0
            if(mp[sum-k])
            {
                ans+=mp[sum-k];
            }
            mp[sum]++;
        }
        return ans;
    }

 力扣974 和可被 K 整除的子数组

同样的模板，只不过数组里面有可能会有负数，所以在除的时候 做一个下标转换

我们只需要知道之前的前缀区间里含有相同余数 （key）的个数。则能够知道当前能够整除 K 的区间个数

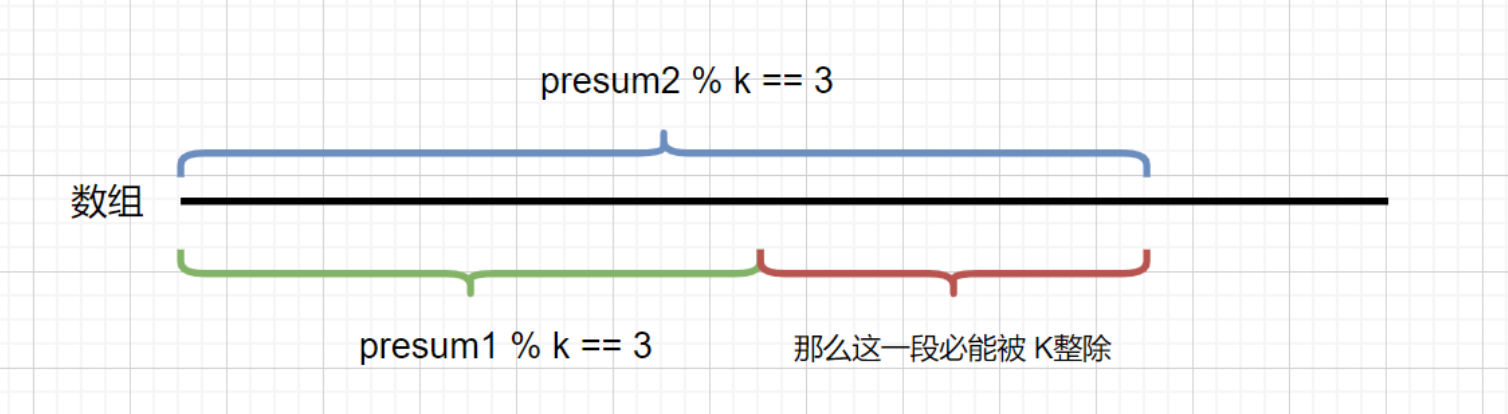
啥意思k等于3，，假如当前我8对3余2，，我只要能找到比8小且+k等于8，且%3也等于2的说明， k就是能被整除的，比如5，，前面要是有个5，那么结果就能++一次

ac:

    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int>mp{{0,1}};
        int sum=0;
        int ans=0;
        for(int i=0;i<nums.size();++i)
        {
            sum+=nums[i];
            //当前 presum 与 K的关系，余数是几，当被除数为负数时取模结果为负数，需要纠正
            int key=(sum%k+k)%k; 
            //查询哈希表获取之前key也就是余数的次数
            if(mp.count(key))
            {
                ans+=mp[key];
            }
            mp[key]++;
        }
        return ans;
    }

力扣523.连续的子数组和

核心一句话：a−b的差值要是k的倍数，那么a除以k的余数必定等于b除以k的余数

也是上一题的核心

这题多了些判断条件

1. 子数组的和本质其实就是两个前缀和的差值，而差值等于n*k,那么意味着这两个前缀和%k是一样的；
2. 那么自然我们就可以保留一个map来记录(前缀和%k) 到对应位置的映射
3. 一旦发现（当前前缀和%k）已经在map里存在，而且两者序号差距大于等于2（满足题目要求子数组大小至少为2），就返回成功
4. 坑：需要考虑前缀和本身就可以被k整除，直接引入一个初始化0->-1,这样子是保证如序号1的时候1-(-1)=2 >=2 这个时候就可以返回结果了
5. 坑：考虑k=0的边界情况

bool checkSubarraySum(vector<int>& nums, int k) {
        unordered_map<int,int>mp{{0,-1}};
         // 防止第一个数和第二个数的和直接是k
         //0 -1
       
        int sum=0;
        for(int i=0;i<nums.size();++i)
        {
              sum+=nums[i];
            int key=(sum)%k; //计算前缀和余数，拿余数去判断
            if(mp.count(key))
            {
                int pos=mp[key];
                if(i-pos>=2){
                    return true;
                }
            }
            else{
                mp[key]=i;
            }
        }
        return false;
    }

over...