状态压缩

这是一个等权无向图，题目要我们求从「一个点都没访问过」到「所有点都被访问」的最短路径。
同时1 <= n <= 12, n 最大只有 12，容易想到使用「状态压缩」来代表「当前点的访问状态」：使用二进制表示长度为 32的 int 的低 12 来代指点是否被访问过。

假设变量 mask存放了「当前点的访问状态」，例如 (000…0101)2 代表编号为 0 和编号为 2 的节点已经被访问过，而编号为 1 的节点尚未被访问。

检查编号为 x 的点是否被访问过时，可以使用位运算 state=(1 << i) & mask，来获取
将标记编号为 x 的节点已经被访问的话，可以使用位运算 mask| (1 << x) 来实现标记。

基于状态压缩的广度优先搜索算法

为什么找到第一个答案时就一定是最短路径了？
或者如Godzil1a所说：正常的Dijstra算法每次选择到未访问的邻接点中最短的，因为权值都是1 所以步数最少一定最短如果权值不为1那么需要找到所有路径然后比较了

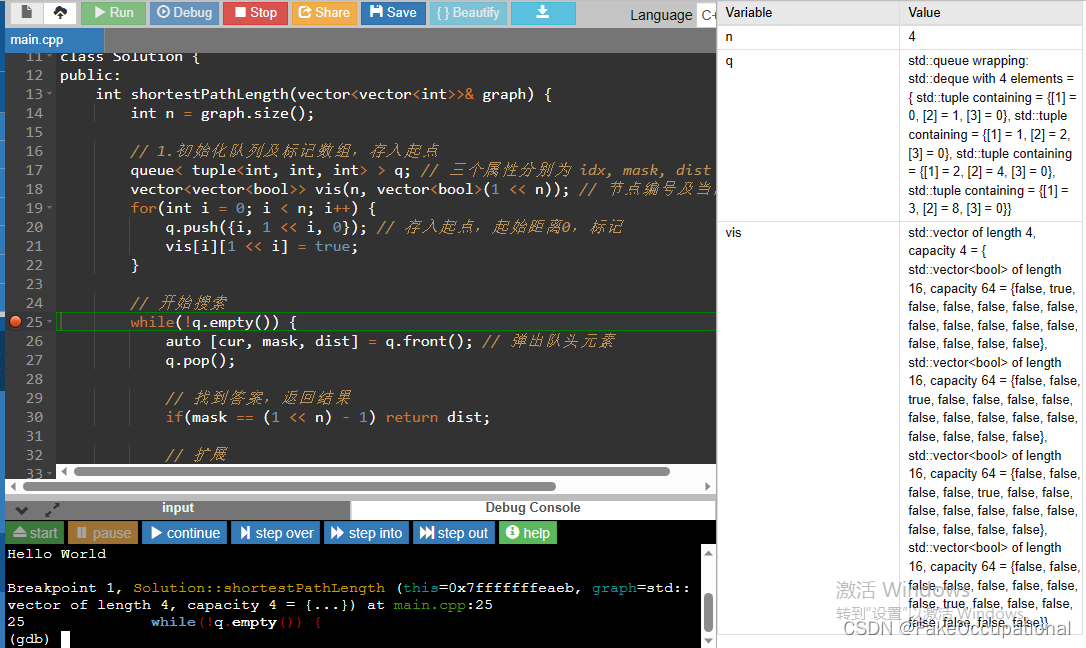
class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();

        // 1.初始化队列及标记数组，存入起点
        queue< tuple<int, int, int> > q; // 三个属性分别为 idx, mask, dist
        vector<vector<bool>> vis(n, vector<bool>(1 << n)); // 节点编号及当前状态
        for(int i = 0; i < n; i++) {
            q.push({i, 1 << i, 0}); // 存入起点，标记，起始距离0,本题将所有点都设置为了起点
            vis[i][1 << i] = true;
        }

        // 开始搜索
        while(!q.empty()) {
            auto [cur, mask, dist] = q.front(); // 弹出队头元素
            q.pop();

            // 找到答案，返回结果
            if(mask == (1 << n) - 1) return dist;

            // 扩展
            for(int x : graph[cur]) {
                int nextmask = mask | (1 << x);
                if(!vis[x][nextmask]) {
                    q.push({x, nextmask, dist + 1});
                    vis[x][nextmask] = true;
                }
            }
        }
        return 0;
    }
};

// 作者：已注销
// 链接：https://leetcode.cn/problems/shortest-path-visiting-all-nodes/solution/gtalgorithm-tu-jie-fa-ba-hardbian-cheng-v5knb/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。




int main()
{
    cout<<"Hello World"<<endl;
    vector<vector<int>> graph = {{1,2,3},{0},{0},{0}};
    Solution solo;
    auto res =  solo.shortestPathLength(graph);
    cout<< res <<"-";
    return 0;
}