1 SVM概述

1.1 概念

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

具体来说就是在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。

SVM使用准则：nn 为特征数，mm 为训练样本数。

如果相较于mm而言，nn要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。
如果nn较小，而且mm大小中等，例如nn在 1-1000 之间，而mm在10-10000之间，使用高斯核函数的支持向量机。
如果nn较小，而mm较大，例如nn在1-1000之间，而𝑚大于50000，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。

1.2 SVM的优缺点

1.2.1 优点

支持向量机算法可以解决小样本情况下的机器学习问题，简化了通常的分类和回归等问题。
由于采用核函数方法克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂性。换句话说，由于支持向量计算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是样本空间的维数。
支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些点对模型学习的影响。

1.2.2 缺点

支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持向量，这其中会涉及m阶矩阵的计算，所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
经典的支持向量机算法只给出了二分类的算法，而在数据挖掘的实际应用中，一般要解决多分类问题，但支持向量机对于多分类问题解决效果并不理想。
SVM算法效果与核函数的选择关系很大，往往需要尝试多种核函数，即使选择了效果比较好的高斯核函数，也要调参选择恰当的参数。另一方面就是现在常用的SVM理论都是使用固定惩罚系数C，但正负样本的两种错误造成的损失是不一样的。

2 在python中使用SVM

2.1 scikit-learn库

Scikit-learn(sklearn）是一个开源项目，可以免费使用和分发，任何人都可以轻松获取其源代码来查看其背后的原理。
scikit-learn是一个非常流行的工具，也是最有名的 Python机器学习库。它广泛应用于工业界和学术界，网上有大量的教程和代码片段。而SVM也可以在scikit-learn库中选择使用。

http:// scikit-learn.org/stable/documentation

2.2 SVM在scikit-learn库中的使用

2.2.1 安装依赖库

1. 安装numpy

! sudo pip install numpy

2. 安装 scipy
   需要先安装 matplotlib ipython ipython-notebook pandas sympy

! sudo apt-get install python-matplotlib ipython ipython-notebook
! sudo apt-get install python-pandas python-sympy python-nose
! sudo pip install scipy

3. 安装 scikit-learn

! sudo pip install -U scikit-learn

2.2.2 svm.SVC

# Create SVM classification object
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)

参数解析：

1. C：惩罚参数。C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
2. kernel：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
3. degree：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。
4. gamma：‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features
5. coef0：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
6. probability：是否采用概率估计。默认为False，布尔类型可选。决定是否启用概率估计。需要在训练fit()模型时加上这个参数，之后才能用相关的方法：predict_proba和predict_log_proba
7. shrinking：是否采用shrinking heuristic方法（启发式收缩），默认为true
8. tol：停止训练的误差值大小，默认为1e-3
9. cache_size：核函数cache缓存大小，默认为200
10. class_weigh： t类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)
11. verbose：允许冗余输出
12. max_iter：最大迭代次数。-1为无限制。
13. decision_function_shape：‘ovo’, ‘ovr’ or None, default=None3
14. random_state：数据洗牌时的种子值，int值。主要调节的参数有：C、kernel、degree、gamma、coef0。

2.2.3 应用实例

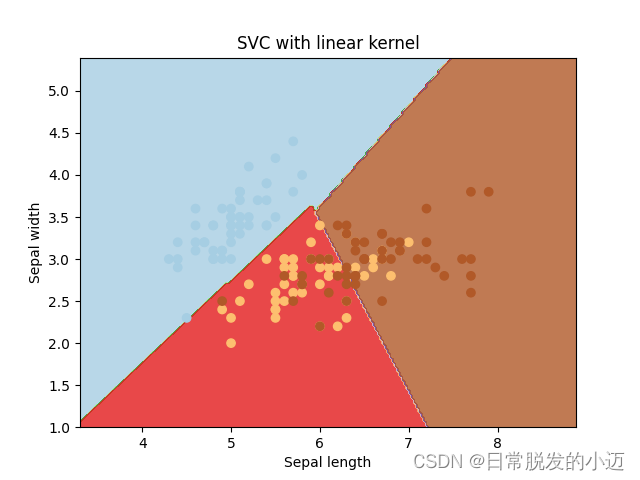
采用鸢尾花数据集，这个数据集包含了150个鸢尾花样本，对应3种鸢尾花，各50个样本，以及它们各自对应的4种关于花外形的数据 ，适用于分类任务。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# 引用 iris 数据集
iris = datasets.load_iris()
X = iris.data[:, :2] # 选取前两列作为X参数
y = iris.target # 采集标签作为y参数
C = 1.0 # SVM regularization parameter

# 将所得参数进行模型训练
svc = svm.SVC(kernel='linear', C=1, gamma='auto').fit(X, y)
# 建图
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
 np.arange(y_min, y_max, h))
plt.subplot(1, 1, 1) # 将显示界面分割成1*1 图形标号为1的网格
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()]) # np.c按行连接两个矩阵,但变量为两个数组，按列连接
Z = Z.reshape(xx.shape)# 重新构造行列
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)# 绘制等高线
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired) # 生成一个scatter散点图。
plt.xlabel('Sepal length') # x轴标签
plt.ylabel('Sepal width') # y轴标签
plt.xlim(xx.min(), xx.max()) # 设置x轴的数值显示范围
plt.title('SVC with linear kernel') # 设置显示图像的名称
plt.savefig('./test1.png') #存储图像
plt.show() # 显示

实现结果如下：

总结

支持向量机是一种分类器。之所以称为”机“是因为它会产生一个二值决策的结果，即它是一种决策”机“。支持向量机是一个二分类器。当其解决多分类问题时需要用额外的方法对其进行扩展。而且SVM的效果也对优化参数和所用核函数中的参数敏感。

---

参考文章：
https://blog.csdn.net/qq_42192693/article/details/121164645