(二叉树) 100. 相同的树 ——【Leetcode每日一题】

news2024/11/18 14:37:52

❓100. 相同的树

难度：简单

给你两棵二叉树的根节点 p 和 q，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

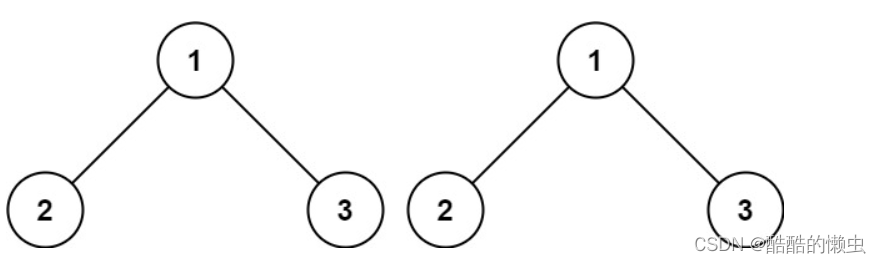
在这里插入图片描述

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

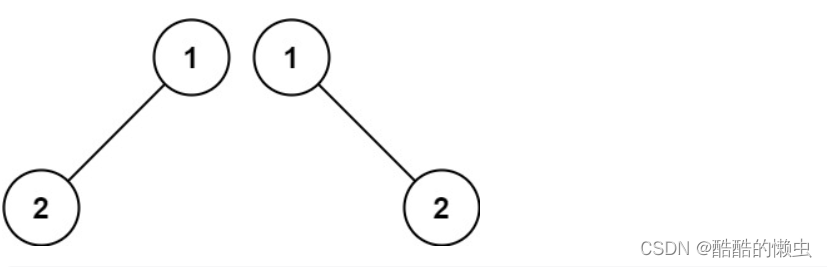
在这里插入图片描述

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

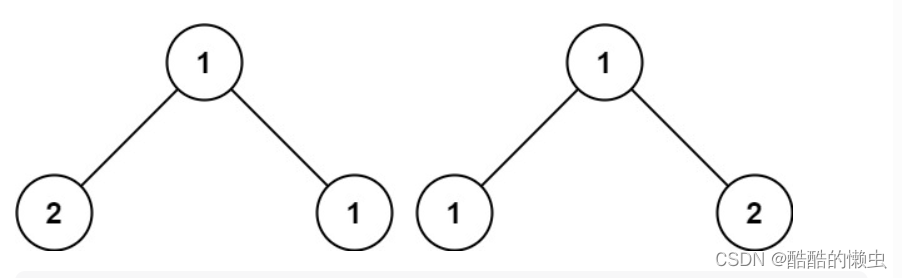
在这里插入图片描述

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 $[0, 100]$ 内
$10^4 <= Node.val <= 10^4$

💡思路：深度优先搜索

如果根节点都为空，返回 true；
如果其中一个为空，或者两个根节点的 val 值不同，则返回 false；
然后递归判断左右子树，如果左右子树都相同时，才返回 true。

🍁代码：(Java、C++)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q == null) return true;
        if((p == null || q == null) || p.val != q.val) return false;
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr) return true;
        if((p == nullptr || q == nullptr) || p->val != q->val) return false;
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (min (m, n))$ ，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。
空间复杂度： $O (min (m, n))$ ，空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。