三维形体投影面积

news2024/10/1 1:26:40

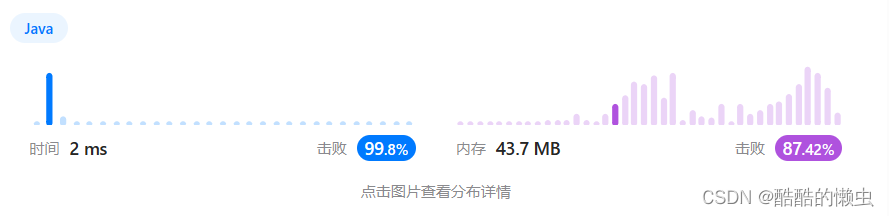
🎈 算法并不一定都是很难的题目，也有很多只是一些代码技巧，多进行一些算法题目的练习，可以帮助我们开阔解题思路，提升我们的逻辑思维能力，也可以将一些算法思维结合到业务代码的编写思考中。简而言之，平时进行的算法习题练习带给我们的好处一定是不少的，所以让我们一起来养成算法练习的习惯。今天练习的题目是一道比较简单的题目 ->三维形体投影面积

问题描述

在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。

投影就像影子，将三维形体映射到一个二维平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回 所有三个投影的总面积 。

示例 1：

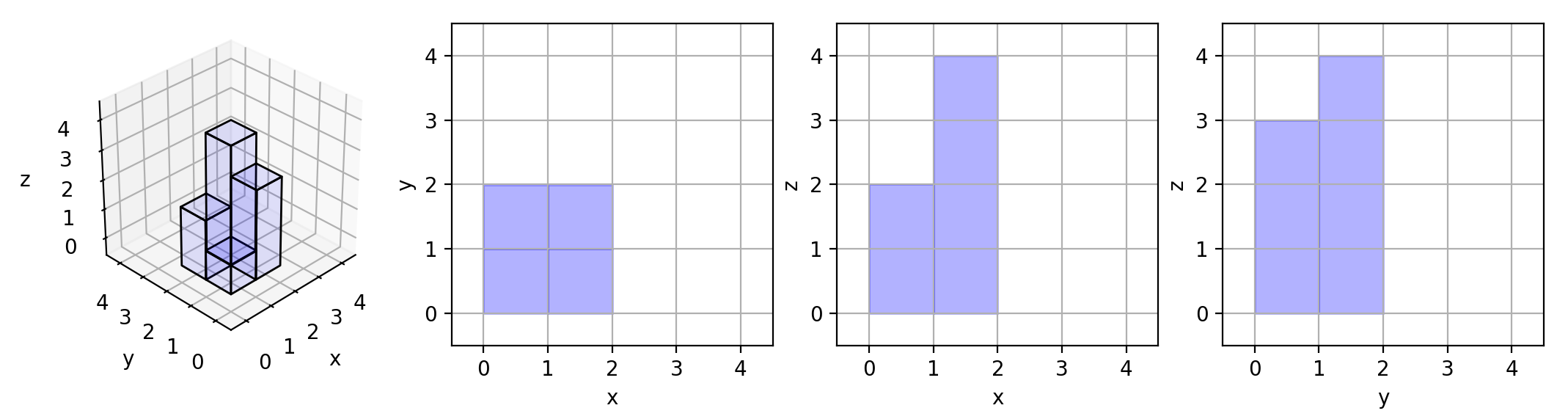
输入： [[1,2],[3,4]]
输出： 17
解释： 这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 2:

输入： grid = [[2]]
输出： 5

示例 3：

输入： [[1,0],[0,2]]
输出： 8

提示：

n == grid.length == grid[i].length
1 <= n <= 50
0 <= grid[i][j] <= 50

思路分析

首先我们应该要先理解一下题目意思，题目会给我们一个二维数组 grid，grid[i]表示第i行排列的每个箱子高度，如示例一：[[1,2],[3,4]]

第一行就是数组 grid[0] = [1,2] ==> 表示两个箱子高度分别是 1、2；

第二行就是数组 grid[1] = [3,4] ==> 表示两个箱子高度分别是 3、4；

我们需要计算这堆箱子分别从顶部、前面和侧面看，我们会看到投射面积之和。

知道了题目的要求和给出参数的含义之后，我们便可以开始编写代码解答题目了，我们可以分为三步，分别计算俯视图、侧视图和正视图面积：

1、计算俯视图面积

俯视图面积是最容易计算的一个，我们只需要遍历数组，找出有箱子的行列数即可（即 grid[i][j] > 0），具体代码如下：

grid.forEach((item) => (res += item.filter((i) => i != 0).length));

2、计算侧视图面积

侧视图其实就是从左边或右边看箱子，这时候我们可以看到的面积取决于每一行中的最高的箱子，所以我们只需要遍历 grid，找出每一行中最高的那个箱子高度，将每一行最高的箱子加起来即是侧视图面积。具体代码如下：

grid.forEach((item) => (res += Math.max(...item)));

3、计算正视图面积

正视图其实就是从前边看箱子，这时候我们可以看到的面积取决于每一列中的最高的箱子，所以我们只需要遍历 grid，找出每一列中最高的那个箱子高度，将每一列中最高的箱子加起来即是正视图面积。具体代码如下：

const map = {};
grid.forEach((item) => {
  item.forEach((cell, cIndex) => {
    map[cIndex] = Math.max(map[cIndex] || 0, cell);
  });
});
for (const key in map) res += map[key];

AC 代码

完整 AC 代码如下：

/**
 * @param {number[][]} grid
 * @return {number}
 */
var projectionArea = function (grid) {
  let res = 0;
  //俯
  grid.forEach((item) => (res += item.filter((i) => i != 0).length));
  //侧
  grid.forEach((item) => (res += Math.max(...item)));
  //正
  const map = {};
  grid.forEach((item) => {
    item.forEach((cell, cIndex) => {
      map[cIndex] = Math.max(map[cIndex] || 0, cell);
    });
  });
  for (const key in map) res += map[key];
  return res;
};