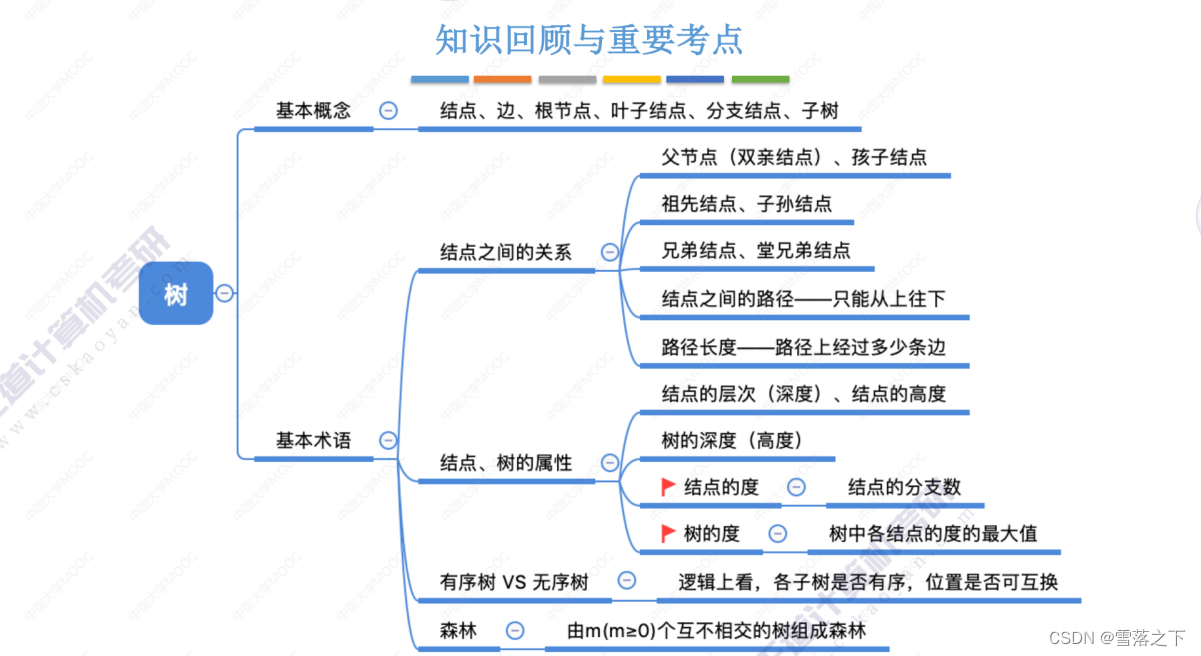
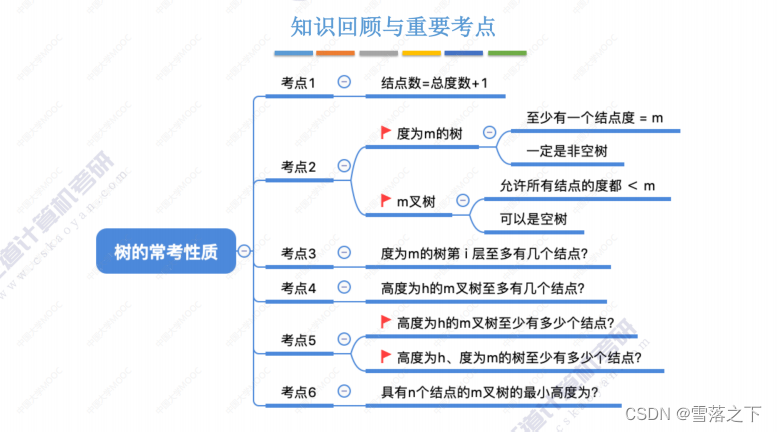
树的基本概念
树是一种非线性的数据结构,它由节点(node)和边(edge)组成。树的基本概念包括以下要点:
- 树由一个根节点(root)开始,根节点没有父节点,它可以有零个或多个子节点。
- 每个节点可以有零个或多个子节点,子节点之间没有顺序关系。
- 除了根节点之外,每个节点有且仅有一个父节点。
- 如果一个节点没有子节点,它被称为叶节点(leaf)或终端节点(terminal node)。
- 节点之间的连接线称为边,边表示节点之间的关系。
树具有层次性的结构,节点和边的关系形成了树的拓扑结构。
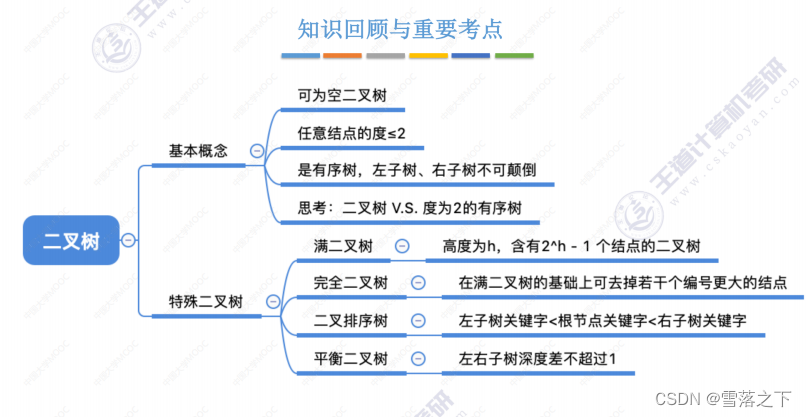
二叉树的基本概念与逻辑结构
二叉树是一种特殊的树结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的基本概念包括以下要点:
- 每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 二叉树中的子树也是二叉树,且子树的位置可以是左子树或右子树。
- 二叉树的子节点没有顺序关系,即左子节点和右子节点可以互换位置而得到相同的二叉树。
二叉树的逻辑结构可以用递归方式定义为一个节点加上两个二叉树的集合,即:
二叉树 = 节点 + 左子树 + 右子树
二叉树的存储结构
二叉树的存储结构主要有两种方式:链式存储和顺序存储。
-
链式存储:每个节点使用一个包含数据和指向左右子节点的指针的结构体来表示。通过指针将各个节点连接起来,形成一个链式结构。链式存储灵活,适用于任意形状的二叉树。
-
顺序存储:使用数组来表示二叉树的节点,按照层次遍历的顺序存储节点的数据。对于某个节点的索引为i,它的左子节点的索引为2i,右子节点的索引为2i+1。顺序存储简单高效,适用于完全
二叉树。
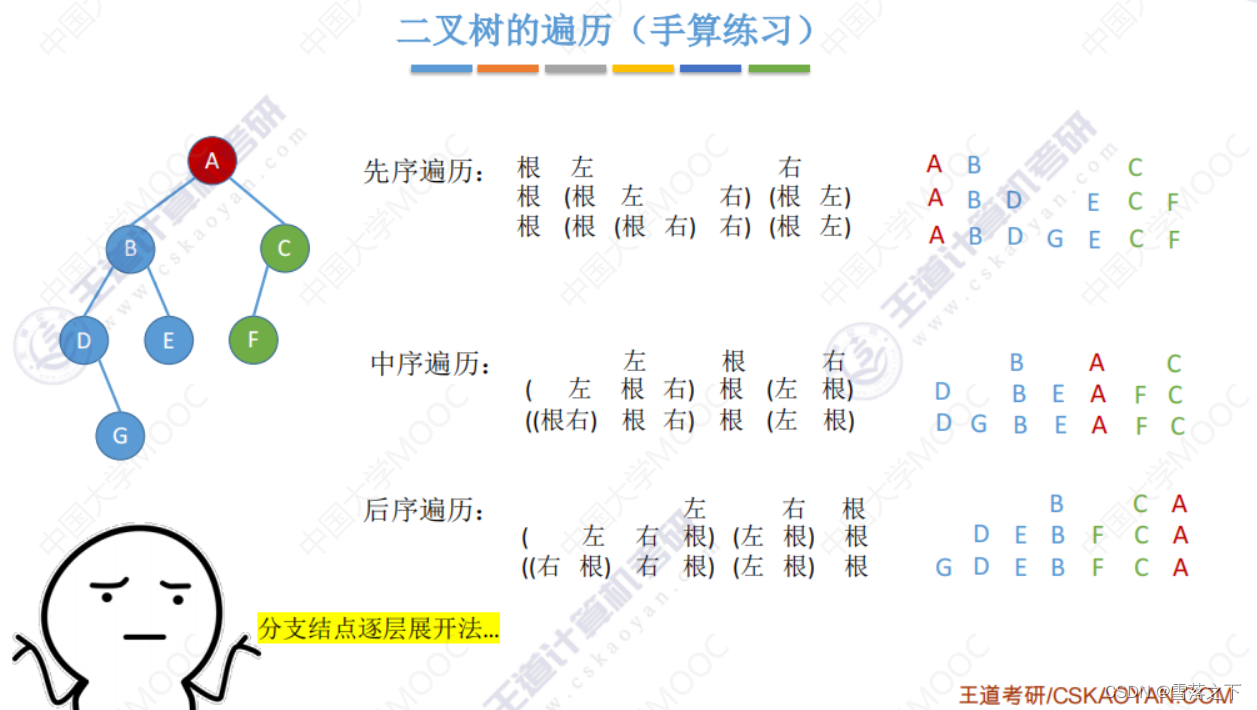
操作 1:遍历二叉树
遍历二叉树是指按照一定规则访问二叉树的所有节点,常用的遍历方式有三种:
- 前序遍历(Preorder Traversal):先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
- 中序遍历(Inorder Traversal):先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
- 后序遍历(Postorder Traversal):先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
遍历二叉树的操作可以使用递归或栈来实现。
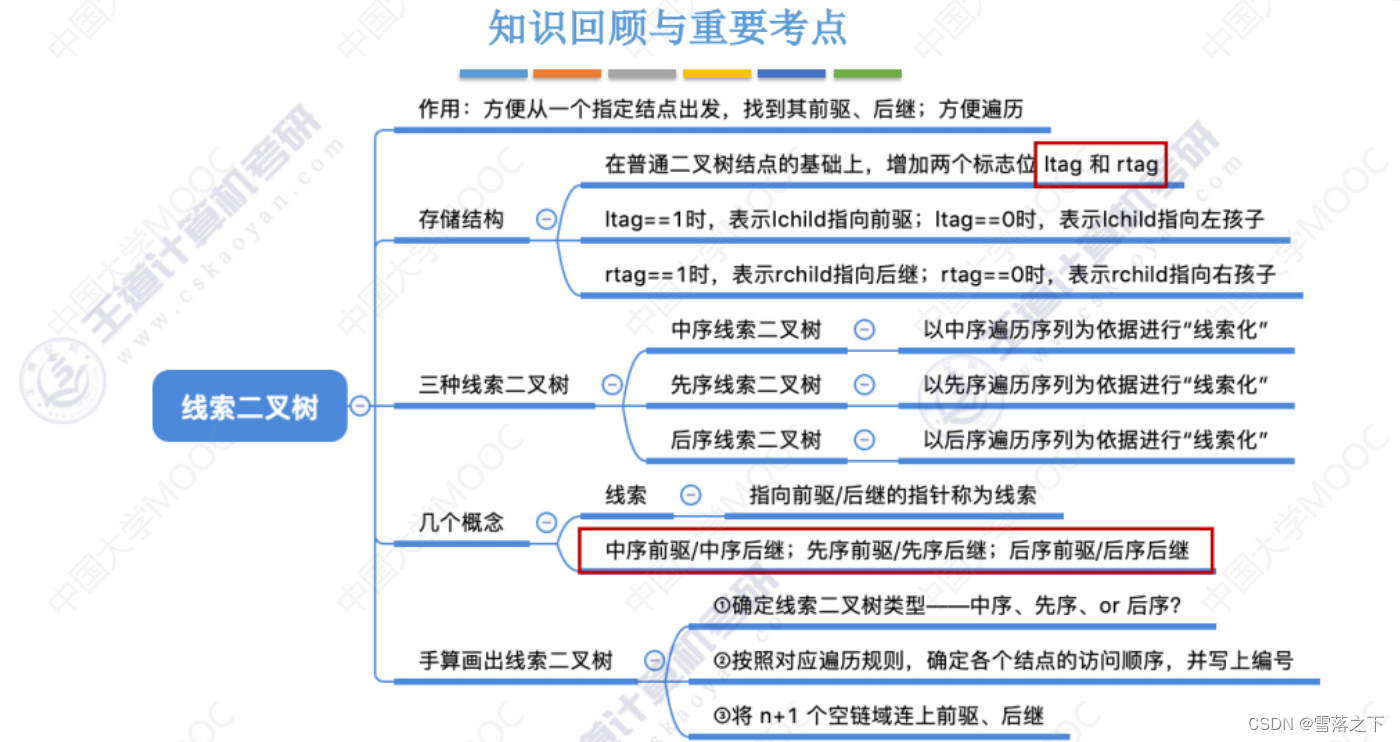
操作 2:线索二叉树
线索二叉树是在二叉树的基础上,利用空指针的空闲域或者指针域指向前驱节点或后继节点,形成一种特殊的二叉树结构。
- 前序线索二叉树:在前序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
- 中序线索二叉树:在中序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
- 后序线索二叉树:在后序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
线索二叉树可以提高遍历二叉树的效率,可以快速找到一个节点的前驱节点或后继节点。
操作 3:哈夫曼树及其应用
哈夫曼树是一种特殊的二叉树,常用于数据压缩和编码算法中。哈夫曼树的特点是权值较大的节点离根节点较近,权值较小的节点离根节点较远。
构建哈夫曼树的步骤:
- 将所有节点按照权值从小到大进行排序。
- 取出权值最小的两个节点作为左右子节点,构建一个新的父节点,父节点的权值为左右子节点的权值之和。
- 将新构建的父节点插入原节点集合中,并删除原来的两个子节点。
重复步骤2和3,直到节点集合中只剩下一个根节点为止。
哈夫曼树的应用主要是通过构建哈夫曼树来实现数据的压缩和解压缩,使得压缩后的数据占用更少的存储空间。
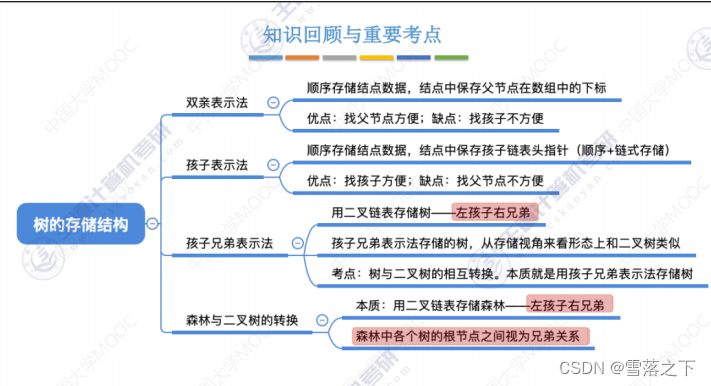
操作 4:二叉树、树和森林相互转换
- 二叉树转换为树:对于任意一个节点的左子节点,将它的右子节点作为它的兄弟节点,然后将其转化为树结构。
- 树转换为二叉树:对于任意一个节点的兄弟节点,将它的右兄弟节点作为它的右子节点,然后将其转化为二叉树结构。
- 森林转换为二叉树:将森林中的每个树转换为二叉树,然后将它们连接起来形成一个二叉树结构。
- 二叉树转换为森林:将二叉树中的每个子树转换为树结构,然后将它们分离开形成森林。
这些转换操作可以通过调整节点的指针关系来实现,从而在二叉树、树和森林之间相互转换。