前言

说起信号与系统，它是一门专业基础课，信号与系统是后期学习数字信号处理、通信原理、自动控制、移动通信课程的基础。
信号与系统它是专业课，但是更像是专业课程中的数学课，涉及到的数学公式很多。我学习了这一门课程让我明白了数学是描述物理现象的一个工程语言，精密、严谨，又简单，可以说数学的一个函数，便是一个信号。
信号与系统说得专业一些就是：一个或几个独立变量函数的信号都包含了某些相关现象的性质信息，而系统总是对给定的信号做出响应，从而产生另外的信号，或者产生某些所需的性质。电路作为时间函数的电压和电流就是信号的一个例子，而电路本身就是一个系统，这时电路对外加电压和电流做出响应便是信号的响应。再举一个例子，当驾驶汽车踩油门的时候，汽车的反应是加速，这时系统就是这部汽车，油门上的压力就是系统的输入，汽车的速度便是系统的响应。
学习信号与系统应该先学习高等数学、复变函数、电路分析、大学物理等知识，课程涉及到微积分、微分方程、线性代数、复变函数、泛函分析等知识，很多的数学概念会在这么课程中结合工程进行应用和介绍。
现如今，MATLAB已经发展成集科学计算、可视化与编程一体的高性能科学工程计算语言和编程开发环境，是目前世界上最流行、应用最为广泛的工程计算和仿真软件之一，几乎成为各类科学研究和工程应用中的标准工具。
本篇文章用于信号与系统在MATLAB中应用学习笔记整理而来，目的为了理解和消化基本信号与系统理论知识。

一、基本信号表示

MATLAB提供了一系列用于表示基本信号的函数，比如：

• square(周期方波)
• sawtooth(周期锯齿波)
• rectpuls(非周期矩形脉冲)
• esp(指数信号)
• sinc(抽样函数)
• sin(正弦信号)
• cos(余弦信号)

1、周期方波信号

t=0:0.01:5;                 %t从0-5，步长为0.01
y=square(4*pi*t);           %产生一个周期方波
plot(t,y);                  %绘制当前二维平面图
title('周期方波');           %标题
xlabel('x');                %x轴
ylabel('y');                %y轴
grid on;                    %显示坐标网格线
xlim([-1 6]);               %设置x轴范围
ylim([-1.5 1.5]);           %设置y轴范围

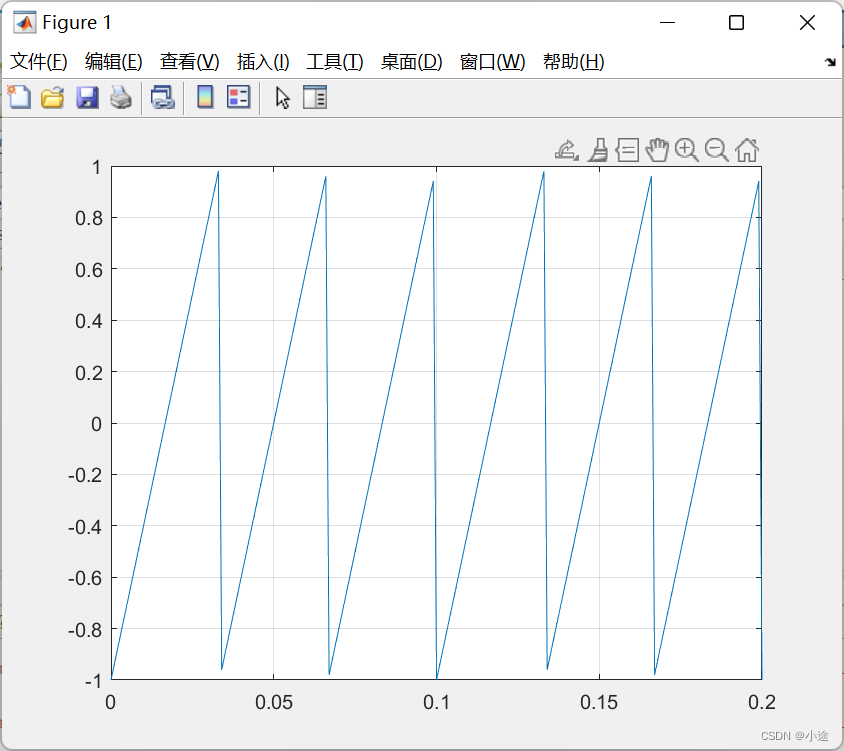
2、周期锯齿波信号

t=0:0.001:2.5;
y=sawtooth(2*pi*30*t);
plot(t,y)
axis([0 0.2 -1 1])
grid on;

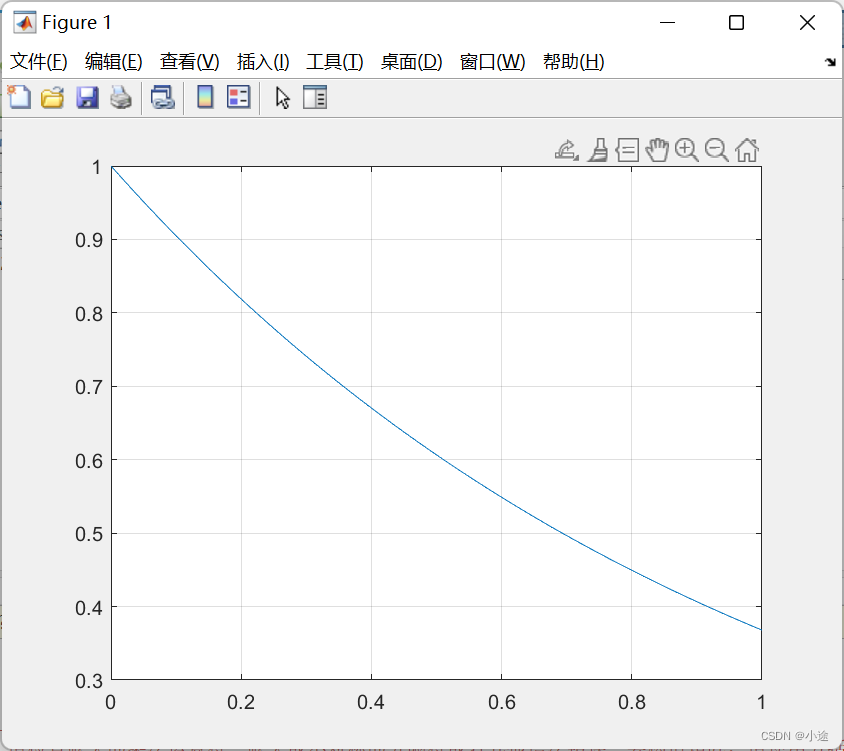
3、指数函数信号

x=linspace(0,1);%生成线性间距向量
%x=0:0.01:1;
y=exp(-x);
plot(x,y);
grid on;

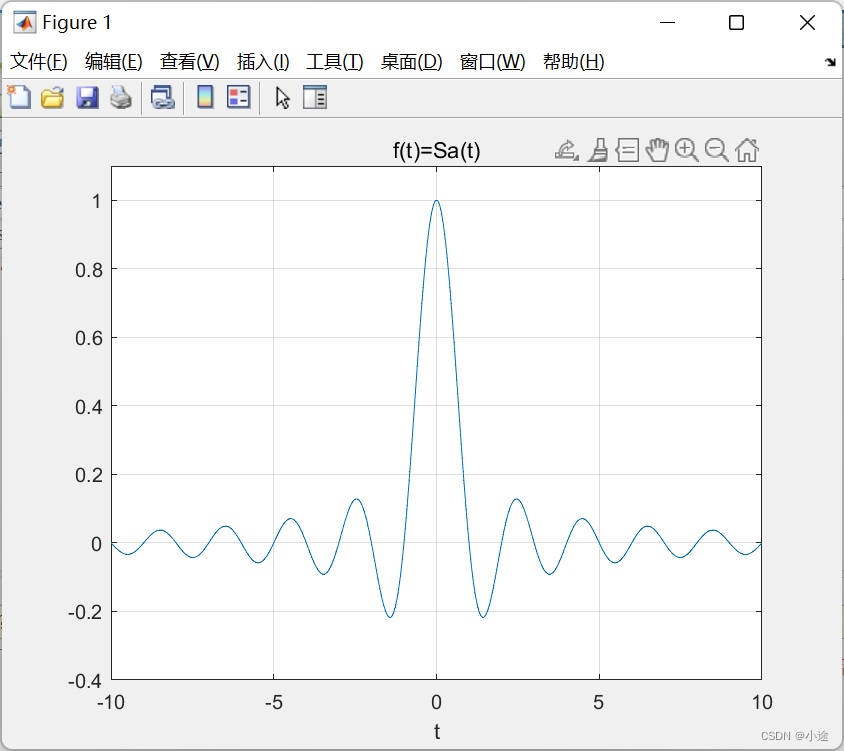
4、抽样函数信号

t=-10:0.01:10;      %向量t时间范围t=t1:p:t2,p为时间间隔
f=sinc(t);   	    %sinc(t)=sin(pi*t)/pi*t
plot(t,f);          %显示该信号的时域波形
title('f(t)=Sa(t)');
xlabel('t')
axis([-10,10,-0.4,1.1]);
grid on;

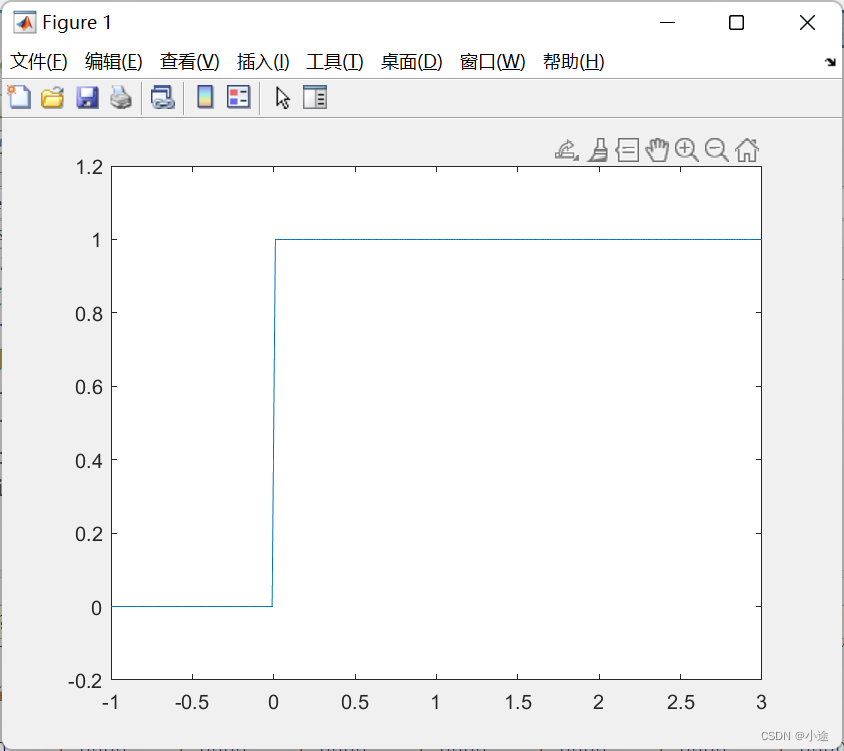
5、单位阶跃信号

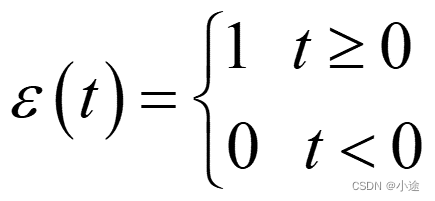
%定义阶跃函数
function f=heaviside(t);
%调用阶跃函数
t=-1:0.01:3;
f=heaviside(t);
plot(t,f);
axis([-1,3,-0.2,1.2]);

二、信号的基本运算

1、信号的相加和相乘

信号的相加是指若干信号之和，表示为
$$f(t)=f_1(t)+f_2(t)+...+f_n(t)$$
其相加的规则为：同一瞬时各信号的函数值和相加构成和信号在这一时刻的瞬时值。
信号相乘是指若干个信号之积，表示为
$$f(t)=f_1(t)\cdot f_2(t)\cdot ...\cdot f_n(t)$$

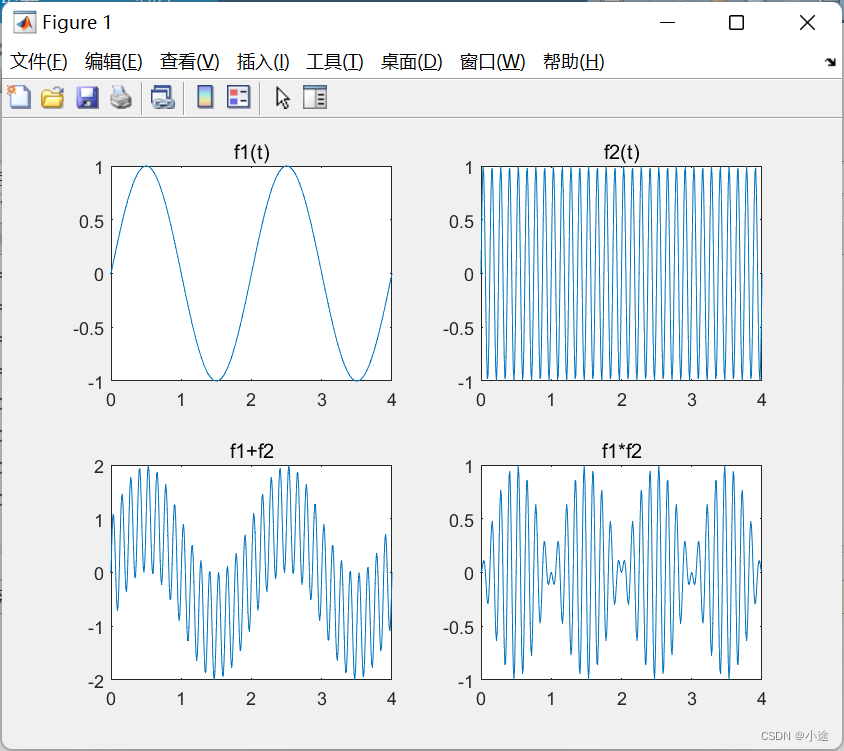
f1=sin(pi*t);
f2=sin(16*pi*t);
f3=f1+f2;
f4=f1.*f2;
subplot(2,2,1);plot(t,f1);title('f1(t)');
subplot(2,2,2);plot(t,f2);title('f2(t)');
subplot(2,2,3);plot(t,f3);title('f1+f2');
subplot(2,2,4);plot(t,f4);title('f1*f2');

2、信号的平移

信号的平移是指信号f(t)变化为信号$f(t+t_0)(t>0)$的运算。若为$f(t+t_0)$,表示信号f(t)沿t轴负方向平移$t_0$时间；若为$f(t-t_0)$，表示信号$f(t)$沿t轴正方向平移$t_0$时间。
可以记为左加右减。
课本上的知识，我可以以初中学到一次函数进行举例，首先复习一下一次函数的概念：

1、一般地，如果y＝kx＋b(k，b是常数，k≠0)，那么y叫做x的一次函数。
2、特别地，当b＝0时，一次函数y＝kx＋b就成为y＝kx(k是常数，k≠0)，这时y叫做x的正比例函数．

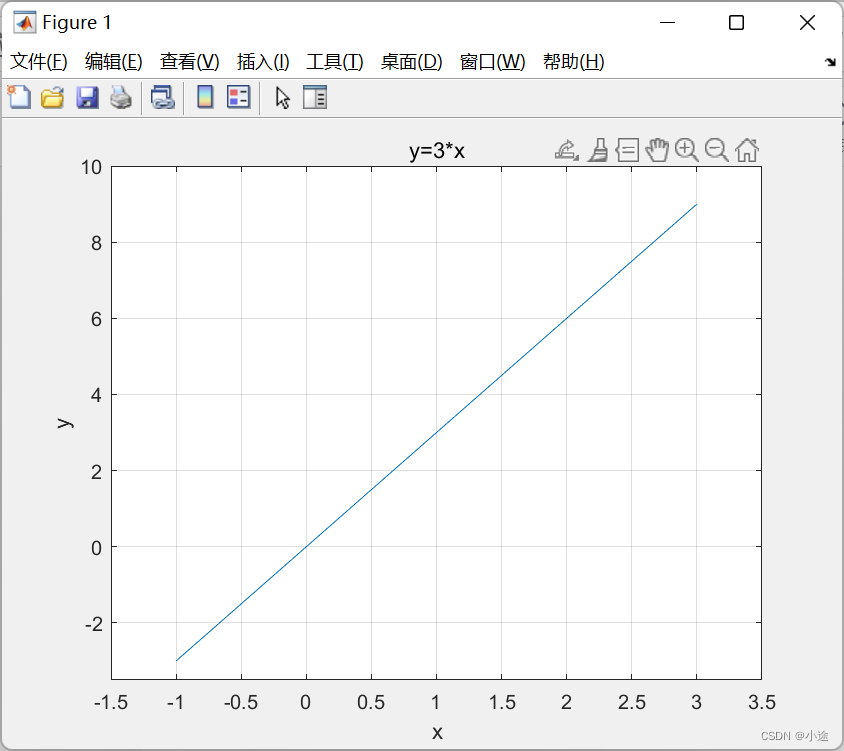
以y=3x为例，x的取-1~3，计算结果、函数图像、MATLAB程序如下

x	y=3x
-1	-3
0	0
1	3
2	6
3	9

x=-1:0.1:3;
y=3*x;
plot(x,y);
title('y=3*x');
ylabel('y');
xlabel('x');
grid on;
axis([-1.5,3.5,-3.5,10]);

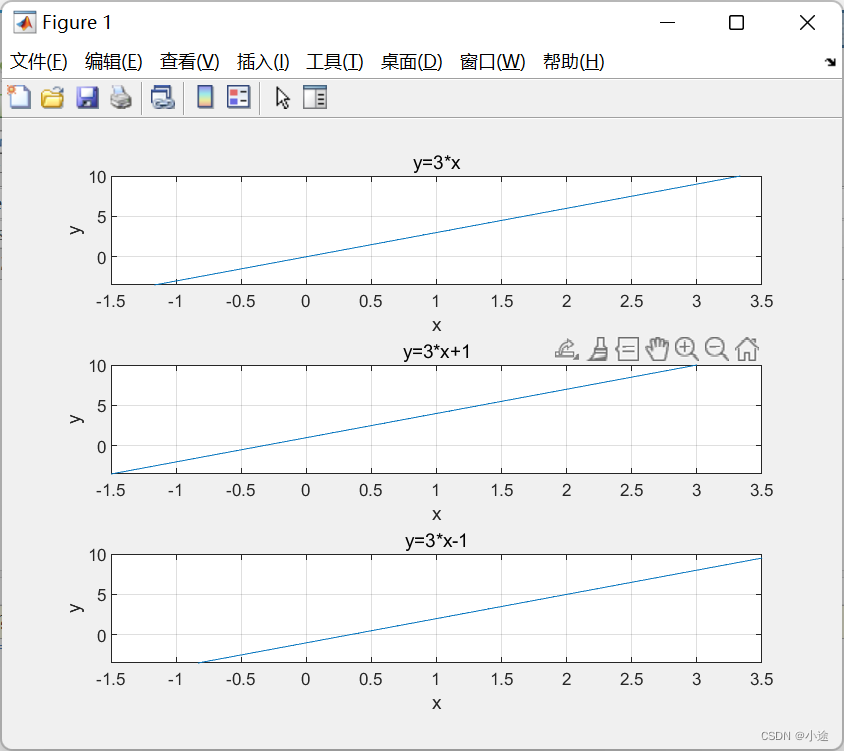
再以y=3x为例，求y=3x+1和y=3x-1，计算结果取-1~3，结果、MATLAB程序、图形如下

x	y=3x+1
-1	-2
0	1
1	3
2	7
3	10

x	y=3x+1
-1	-4
0	-1
1	2
2	5
3	8

x=-5:0.1:5;
y=3*x;
y2=3*x+1;
y3=3*x-1;

subplot(311);
plot(x,y);
title('y=3*x');
ylabel('y');
xlabel('x');
grid on;
axis([-1.5,3.5,-3.5,10]);

%超前
subplot(312);
plot(x,y2);
title('y=3*x+1');
ylabel('y');
xlabel('x');
grid on;
axis([-1.5,3.5,-3.5,10]);

%滞后
subplot(313);
plot(x,y3);
title('y=3*x-1');
ylabel('y');
xlabel('x');
grid on;
axis([-1.5,3.5,-3.5,10]);

以上使用初中生都会的一次函数举例就是为了更好的理解信号平移的概念，也正像我之前说的信号即是函数的概念，而解函数便是解信号与系统。
同理，以教科书上的例题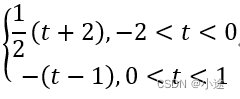求f(t+1)，f(t-1)

解析：这个函数其实便是高中学习的分段函数，分段函数的定义是：一个函数，其定义域内，对于自变量的不同取值区间，有不同的对应方式。分段函数的解析式由几个解析式构成，并不是说分段函数是几个函数，分段函数是一个函数，其解析式一起用花括号联立，注明自变量的取值范围。分段函数的定义域是各段函数定义域的并集，值域也是各段函数值得并集。考虑到一些基础差的同学，如果分段函数不了解，可以到网上找一些资源来学习一下。

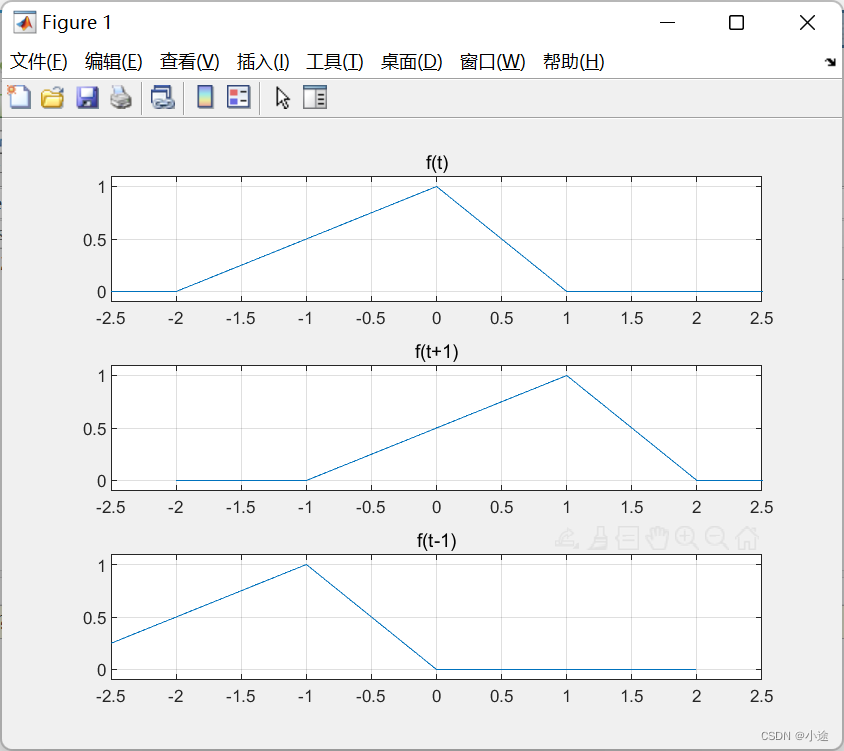
下面我使用MATLAB来描述这个分段函数信号。

t=-3:0.01:3;
ft=1/2*(t+2).*(-2<t&t<0)+(-(t-1)).*(0<=t&t<1);

subplot(311);
plot(t,ft);
title('f(t)');
grid on;
axis([-2.5,2.5,-0.1,1.1]);

%超前
subplot(312);
plot(t+1,ft);
title('f(t+1)');
grid on;
axis([-2.5,2.5,-0.1,1.1]);

%滞后
subplot(313);
plot(t-1,ft);
title('f(t-1)');
grid on;
axis([-2.5,2.5,-0.1,1.1]);

3、信号的反折

信号的反折是指信号f(t)变化为f(-t)的运算。从几何意义上来看，即是将f(t)以纵轴（y轴）为中心做180°的翻转。
再以一次函数y=3x举例，求出y=3(-x)

x=-5:0.1:5;
y=3*x;
y2=3*-1*x;

subplot(211);
plot(x,y);
title('y=3*x');
ylabel('y');
xlabel('x');
grid on;
axis([-10,10,-3.5,10]);

subplot(212);
plot(x,y2);
title('y=3*-1*x');
ylabel('y');
xlabel('x');
grid on;
axis([-10,10,-3.5,10]);

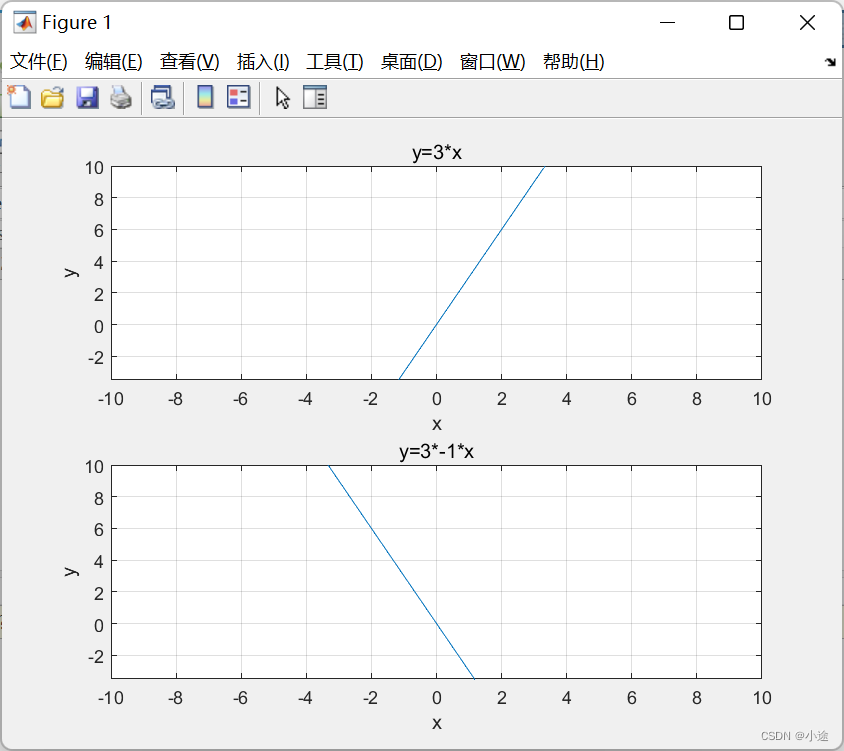
通过图像可以看到，函数关于原点对称。
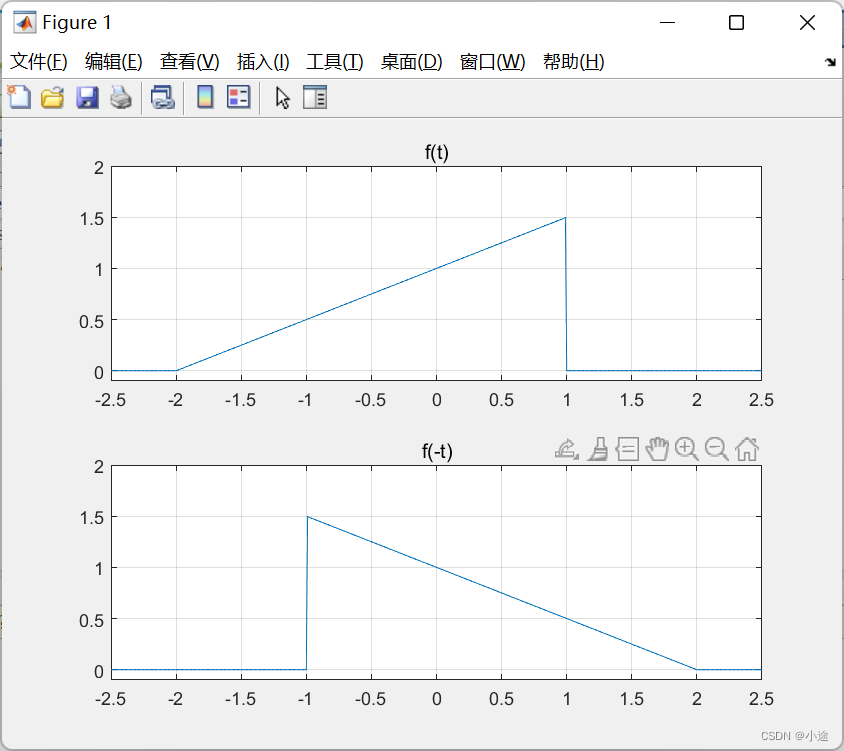
同理，以教科书上的例题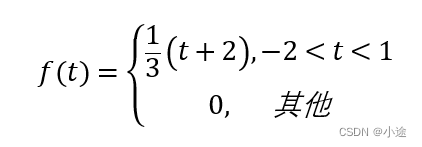求出对应波形的f(-t)

t=-3:0.01:3;
ft=1/2*(t+2).*(-2<t&t<1);
subplot(211);
plot(t,ft);
title('f(t)');
grid on;
axis([-2.5,2.5,-0.1,2]);

%反折
subplot(212);
plot(-1*t,ft);
title('f(t)');
grid on;
axis([-2.5,2.5,-0.1,2]);

4、信号的尺度变换（缩展）

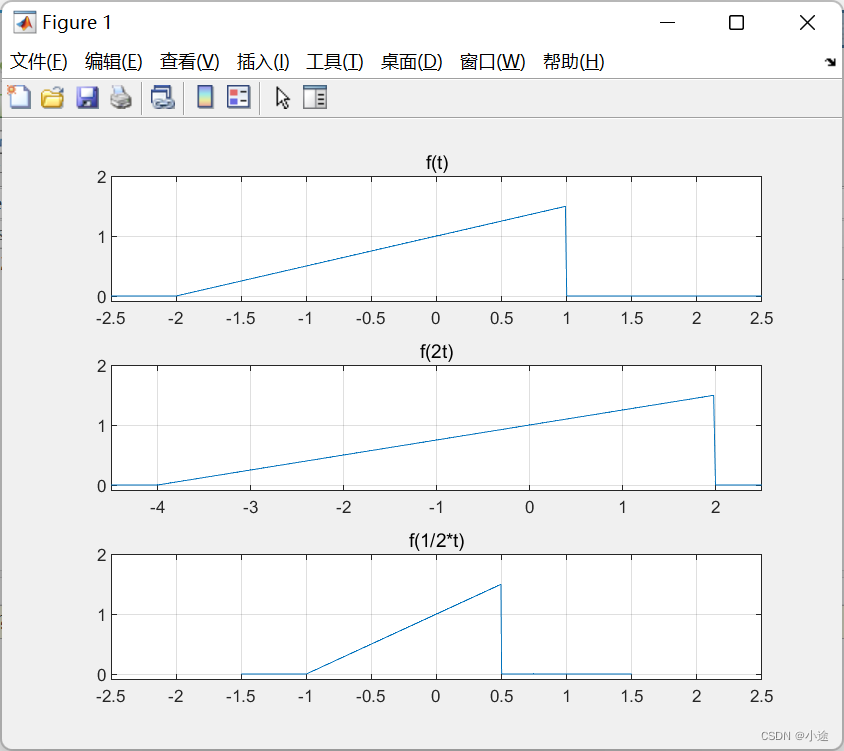
这段知识如果放到高中数学来说便是函数图像的伸缩变换，在信号与系统中，信号的尺度变换是将信号f(t)变换为f(at)(a>0)的运算。若0<a<1，则将f(t)以原点为基准，沿横坐标轴展宽1/a倍；若a>1，则将f(t)沿横坐标压缩至1/a倍。
同样，以这个例函数为例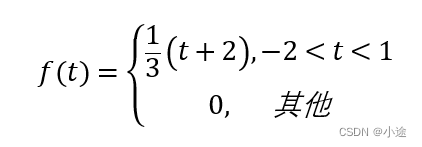
分别求f(2t)和f(1/2*t)的波形。

t=-3:0.01:3;
ft=1/2*(t+2).*(-2<t&t<1);
subplot(311);
plot(t,ft);
title('f(t)');
grid on;
axis([-2.5,2.5,-0.1,2]);

subplot(312);
plot(2*t,ft);
title('f(2t)');
grid on;
axis([-4.5,2.5,-0.1,2]);

subplot(313);
plot(1/2*t,ft);
title('f(1/2*t)');
grid on;
axis([-2.5,2.5,-0.1,2]);

5、信号的微分和积分

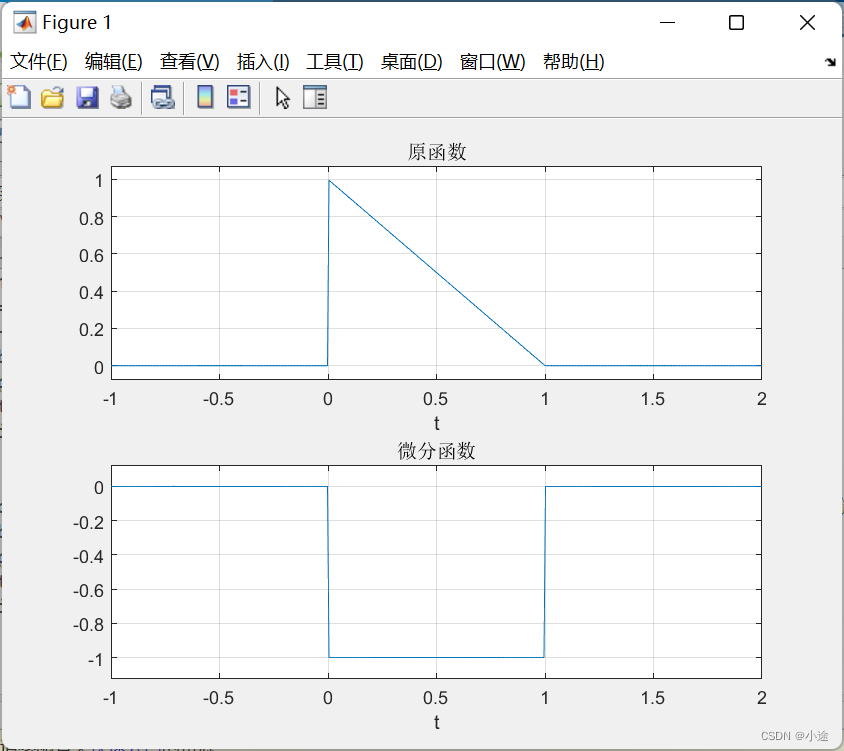
到了这一块内容，就需要用到高等数学的求导和积分的公式了，关于信号的微分即是对信号f(t)求导数，体现信号的变化，表示为
$$y(t)=df(t)/dt=f^{\prime }(t)$$
信号的积分即是对信号在(-∞,t)上的积分，用于与平滑信号的变化，表示为

例题：求信号$f(t)=(1-t)[\epsilon (t)-\epsilon (t-1)]$的积分和微分

syms t f2;                                          %定义符号变量？
f2=(1-t).*(heaviside(t)-heaviside(t-1));
t=-1:0.01:2;                                        %定义变量t的范围
subplot(211);
ezplot(f2,t);
title('原函数')
grid on


f=diff(f2,'t',1);                                   %对函数f2中的变量t进行一次微分（即求一阶导数）
subplot(212)
ezplot(f,t);
title('微分函数')
grid on

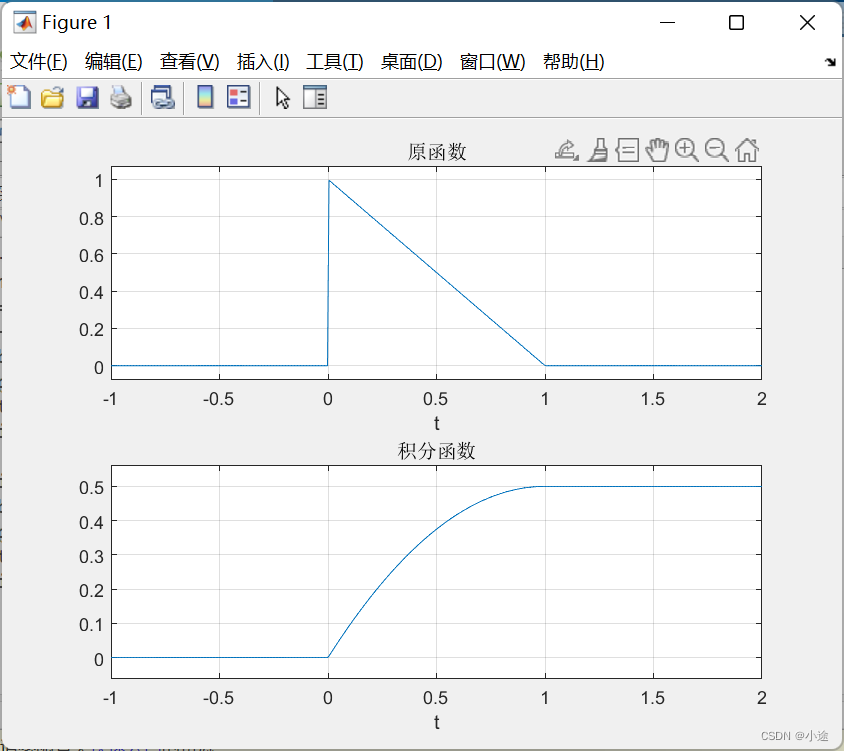
syms t f1;                                          %定义符号变量
f1=(1-t).*(heaviside(t)-heaviside(t-1));
t=-1:0.01:2;                                        %定义变量t的范围
subplot(211);
ezplot(f1,t);
title('原函数')
grid on

f=int(f1,'t');                                      %对函数f1中的变量t进行积分
subplot(212)
ezplot(f,t);
title('积分函数')
grid on

未完待续…