轨迹博客：

玫瑰线轨迹如何规划？（desmos+ROS2+turtlesim+……）

ROS1云课→23turtlesim绘制小结（数学和编程）

---

如上所涉及的机器人假定模型都是差动驱动机器人。

许多移动机器人使用一种称为差动驱动的驱动机构。它由安装在公共轴上的两个驱动轮组成，每个轮可以独立地向前或向后驱动。

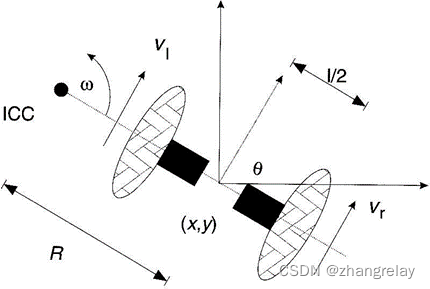
图1:差动驱动运动学-Dudek和Jenkin《移动机器人的计算原理》

机器人旋转的点被称为ICC -瞬时曲率中心

通过改变两个轮子的速度，可以改变机器人的轨迹。

这类驱动器有三个有趣的例子：

1. 直线运动，左右轮速度一样
2. 绕轮轴的中点旋转，也就是原地旋转，左右轮速度大小一样，方向相反。
3. 绕某一轮为中心旋转，左轮或右轮只有一轮有速度

注意，差动驱动机器人不能沿着轴的方向移动——这是一个奇点。

曲线上存在不可导、不连续、根本没有定义的点，这些点就叫做奇点。基本上来说求导就可以瑕点是函数趋于无穷的点；奇点是函数未定的点。比如间断点，无定义点。奇点包含瑕点。

机器人系统数学建模（现代控制理论1）

图2 差动机器人数学建模

差速驱动车辆对每个车轮速度的微小变化非常敏感。轮子之间相对速度的差异会影响机器人的轨迹。它们对地平面的微小变化也非常敏感，可能需要额外的轮子(脚轮)来支撑。

凹凸不平的地面会影响轨迹精度。

差动驱动机器人的正向运动学

在图1中，假设机器人在某个位置(x，y)，朝向与X轴成θ角的方向。假设机器人的中心位于轮轴的中点。通过操纵控制参数Vl、Vr，可以使机器人移动到不同的位置和方向。(注:Vl，Vr)为车轮沿地面的速度)。

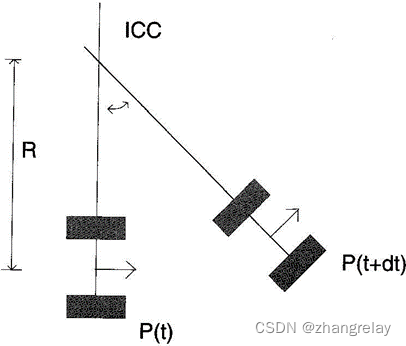
图3:差动机器人的正向运动学 

移动机器人的逆运动学

如何控制机器人达到给定的位置(x，y，θ)——这就是所谓的逆运动学问题。

不幸的是，差动驱动机器人在建立其位置时符合所谓的非完整约束。例如，机器人不能沿着它的轴横向移动。类似的非完整约束是汽车只能转动前轮。它不能直接侧向移动，因为平行泊车（侧方位停车）需要更复杂的转向操作。因此，不能简单地指定一个任意的机器人姿态(x，y，θ)并找到控制机器人所需要的速度。

这激活了机器人沿直线移动，然后原地旋转一圈，然后再次直线移动的策略，作为差动驱动机器人的导航策略。

直线运动轨迹：

圆周运动轨迹： 

未闭合

 闭合后，但控制为开环，也就是没有反馈控制。

正方形运动轨迹（非连续控制）： 

 可参考官方示例代码：

#include <rclcpp/rclcpp.hpp>
#include <turtlesim/msg/pose.hpp>
#include <geometry_msgs/msg/twist.hpp>
#include <std_srvs/srv/empty.hpp>
#include <math.h>

turtlesim::msg::Pose::SharedPtr g_pose;
turtlesim::msg::Pose g_goal;

enum State
{
  FORWARD,
  STOP_FORWARD,
  TURN,
  STOP_TURN,
};

State g_state = FORWARD;
State g_last_state = FORWARD;
bool g_first_goal_set = false;

#define PI 3.141592

void poseCallback(const turtlesim::msg::Pose::SharedPtr pose)
{
  g_pose = pose;
}

bool hasReachedGoal()
{
  return fabsf(g_pose->x - g_goal.x) < 0.01 && fabsf(g_pose->y - g_goal.y) < 0.01 && fabsf(g_pose->theta - g_goal.theta) < 0.002;
}

bool hasStopped()
{
  return g_pose->angular_velocity < 0.0001 && g_pose->linear_velocity < 0.0001;
}

void printGoal()
{
  RCLCPP_INFO(rclcpp::get_logger("draw_square"), "New goal [%f %f, %f]", g_goal.x, g_goal.y, g_goal.theta);
}

void commandTurtle(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub, float linear, float angular)
{
  geometry_msgs::msg::Twist twist;
  twist.linear.x = linear;
  twist.angular.z = angular;
  twist_pub->publish(twist);
}

void stopForward(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub)
{
  if (hasStopped())
  {
    RCLCPP_INFO(rclcpp::get_logger("draw_square"), "Reached goal");
    g_state = TURN;
    g_goal.x = g_pose->x;
    g_goal.y = g_pose->y;
    g_goal.theta = fmod(g_pose->theta + static_cast<float>(PI) / 2.0f, 2.0f * static_cast<float>(PI));
    // wrap g_goal.theta to [-pi, pi)
    if (g_goal.theta >= static_cast<float>(PI)) g_goal.theta -= 2.0f * static_cast<float>(PI);
    printGoal();
  }
  else
  {
    commandTurtle(twist_pub, 0, 0);
  }
}

void stopTurn(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub)
{
  if (hasStopped())
  {
    RCLCPP_INFO(rclcpp::get_logger("draw_square"), "Reached goal");
    g_state = FORWARD;
    g_goal.x = cos(g_pose->theta) * 4 + g_pose->x;
    g_goal.y = sin(g_pose->theta) * 4 + g_pose->y;
    g_goal.theta = g_pose->theta;
    printGoal();
  }
  else
  {
    commandTurtle(twist_pub, 0, 0);
  }
}


void forward(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub)
{
  if (hasReachedGoal())
  {
    g_state = STOP_FORWARD;
    commandTurtle(twist_pub, 0, 0);
  }
  else
  {
    commandTurtle(twist_pub, 1.0f, 0);
  }
}

void turn(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub)
{
  if (hasReachedGoal())
  {
    g_state = STOP_TURN;
    commandTurtle(twist_pub, 0, 0);
  }
  else
  {
    commandTurtle(twist_pub, 0, 0.1f);
  }
}

void timerCallback(rclcpp::Publisher<geometry_msgs::msg::Twist>::SharedPtr twist_pub)
{
  if (!g_pose)
  {
    return;
  }

  if (!g_first_goal_set)
  {
    g_first_goal_set = true;
    g_state = FORWARD;
    g_goal.x = cos(g_pose->theta) * 4 + g_pose->x;
    g_goal.y = sin(g_pose->theta) * 4 + g_pose->y;
    g_goal.theta = g_pose->theta;
    printGoal();
  }

  if (g_state == FORWARD)
  {
    forward(twist_pub);
  }
  else if (g_state == STOP_FORWARD)
  {
    stopForward(twist_pub);
  }
  else if (g_state == TURN)
  {
    turn(twist_pub);
  }
  else if (g_state == STOP_TURN)
  {
    stopTurn(twist_pub);
  }
}

int main(int argc, char** argv)
{
  rclcpp::init(argc, argv);
  auto nh = rclcpp::Node::make_shared("draw_square");
  auto pose_sub = nh->create_subscription<turtlesim::msg::Pose>("turtle1/pose", 1, std::bind(poseCallback, std::placeholders::_1));
  auto twist_pub = nh->create_publisher<geometry_msgs::msg::Twist>("turtle1/cmd_vel", 1);
  auto reset = nh->create_client<std_srvs::srv::Empty>("reset");
  auto timer = nh->create_wall_timer(std::chrono::milliseconds(16), [twist_pub](){timerCallback(twist_pub);});

  auto empty = std::make_shared<std_srvs::srv::Empty::Request>();
  reset->async_send_request(empty);

  rclcpp::spin(nh);
}

开环控制，重复精度不高，效果如下：

 

思考题：

如何绘制如下曲线，选择一款绘制即可。

 

---

-Fin-

---