BFS 广度优先遍历详见搜索与图论-BFS

一、树与图的广度优先遍历

• 树与图的广度优先遍历思想与 BFS 相似，是一层一层地进行搜索。

1. 构建

• 构建方式与上文类似，详见搜索与图论-树与图的深度优先遍历。

2. 遍历

• 广度优先遍历是对临边的搜索，模板代码如下：

void bfs()
{
    int hh = 0,tt = 0;
    q[0] = 1;//队列数组
    
    while(hh <= tt)
    {
        int t = q[hh++];
        
        for(int i = h[t];i != -1;i = ne[i])
        {
            int j = e[i];
            if(判断)
                q[++tt] = j;
        }
    }    
}

• 针对具体的题目，填入对应的代码即可。

3. 具体实现详见例题——图中点的层次

二、树与图的广度优先遍历例题——图中点的层次

题目描述

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环。
所有边的长度都是 1，点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离，如果从 1 号点无法走到 n 号点，输出 −1。

输入格式

第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 a 和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

数据范围

1 ≤ n,m ≤ 1e5

输入样例

4 5
1 2
2 3
3 4
1 3
1 4

输出样例

1

具体实现（一）

1. 样例演示

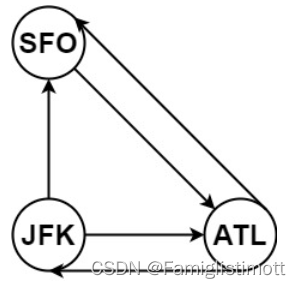
• 重边 是指两个点之间有两条边。如下图所示就叫重边。

• 自环 是指自己指向自己。如下图所示就叫自环。

• 首先，输入两个整数 n=4 和 m=5 。
• 有 m=5 个操作。
• 1 到 2 连一条边。
• 2 到 3 连一条边。
• 3 到 4 连一条边。
• 1 到 3 连一条边。
• 1 到 4 连一条边。
• 求的是 1 号点到 n=4 号点的最短路径，

2. 实现思路

• 判断 1 号点能否走到 n 号点，广度优先遍历即可。
• 用 dist 数组保存 1 号点到各个节点的距离，初始时，都是无穷大。
• 用 st 数组标记各个节点有没有走到过。
• 从 1 号点开始，广度优先遍历：
• （1） 1 号点入队列，dist[1] 的值更新为 0。
• （2） 如果队列非空，就取出队头，找到队头节点能到的所有节点。如果队头节点能到走到的节点没有标记过，就将节点的 dist 值更新为队头的 dist 值 +1 ，然后入队。
• （3） 重复步骤 2 直到队列为空。
• （4） 这个时候，dist 数组中就存储了 1 号点到各个节点的距离了。如果距离是无穷大，则不能到达，输出 -1，如果距离不是无穷大，则能到达，输出距离。
• 图的存储采用邻接表的形式。
• （1） 用 h 数组保存各个节点能到的第一个节点的编号。开始时，h[i] 全部为 -1。
• （2） 用 e 数组保存节点编号，ne 数组保存 e 数组对应位置的下一个节点所在的索引。
• （3） 用 idx 保存下一个 e 数组中，可以放入节点位置的索引。
• （4） 插入边使用的头插法，例如插入：a->b。首先把b节点存入e数组，e[idx] = b。然后 b 节点的后继是h[a]，ne[idx] = h[a]。最后，a 的后继更新为 b 节点的编号，h[a] = idx，索引指向下一个可以存储节点的位置，idx ++ 。

3. 代码注解

• int h[N],ne[N], e[N], idx；邻接表数据结构。
• int dist[N]；存储距离。
• int st[N]；标记点是否走到过。
• memset(dist, 0x3f, sizeof(dist))；初始都没有走到过，距离无穷大。
• cout << (dist[n] == 0x3f3f3f3f ? -1 : dist[n])；如果到 n 号节点的距离不是无穷大，输出距离，如果是无穷大，输出 -1。
• 详细注解见实现代码。

4. 实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int h[N],ne[N], e[N], idx;
int dist[N];
int st[N];
int n, m;

void add(int a, int b)//邻接表存储图
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;//从1号节点开始，距离为0
    queue<int> q;//队列
    q.push(1);//1号节点入队列
    st[1] = 1;//1到1的距离为0，已经求出
    while(q.size())//对列非空，就一直往后搜索
    {
        int t = q.front();//队头出队，找该点能到的点
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i])//遍历所有t节点能到的点，i为节点索引
        {
            int j = e[i];//通过索引i得到t能到的节点编号
            if(!st[j])//如果没有遍历过
            {
                dist[j] = dist[t] + 1;//距离为t号节点的距离+1
                q.push(j);//节点入队
                st[j] = 1;//入队后标记，已经遍历过了
            }
        }
    }
}

int main()
{
    cin >> n >>m;
    memset(h, -1, sizeof h);//初始化，所有节点没有后继，后继都是-1
    for(int i = 0; i < m; i++)//读入所有边
    {
        int a, b;
        cin >> a >> b;
        add(a, b);//加入邻接表
    }
    bfs();//广度优先遍历

    cout << (dist[n] == 0x3f3f3f3f ? -1 : dist[n]);
    system("pause");
    return 0;
}

具体实现（二）

1. 代码注解

• int d[N]；存储每个节点离起点的距离 d[1]=0 。
• int q[N]；存储层次遍历序列 0 号节点是编号为 1 的节点。
• d[j]=d[t]+1；d[j] 存储j节点离起点的距离，并标记为访问过。

2. 实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++ ;
}

int bfs()
{
    int hh = 0;
    int tt = 0;
    q[0] = 1;
    
    memset(d, -1, sizeof d);

    d[1] = 0;
    
    while (hh <= tt)
    {
        int t = q[hh ++];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (d[j] == -1)
            {
                d[j] = d[t] + 1;
                tt ++;
                q[tt] = j;
            }
        }
    }

    return d[n];
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }

    cout << bfs() << endl;

    return 0;
}