14.1 随机梯度下降

假设你正在使用梯度下降来训练一个线性回归模型

 当m个样本的m很大时，求和计算量太大了。这种梯度下降算法有另外一个名字叫做批量梯度下降（batch gradient desent）。这种算法每次迭代需要使用全量训练集，直到算法收敛。

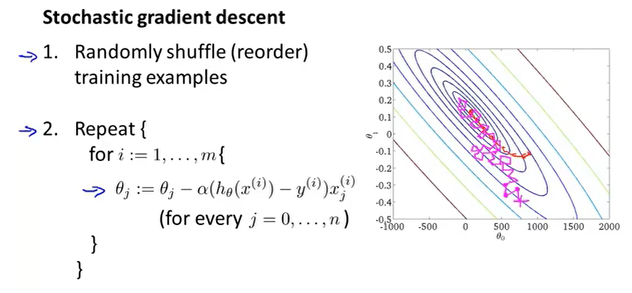
随机梯度下降：

1. 随机打乱所有数据
2. 在i=1...m中进行循环，也就是对所有的训练样本进行遍历，然后更新

随机梯度下降算法对每个数据分开处理，对一个数据更新所有的参数。梯度下降算法是在每次更新参数的时候，需要计算所有数据。对比下来SGD（随机梯度下降）的速度要快一些，不过收敛性可能没GD（梯度下降）好。

如何判断SGD的收敛以及如何选择合适的学习率？

首先定义cost函数，然后每隔1000次迭代画出cost的图像，根据均值来判断；如果噪声太多图像上下震荡，可以选择更多的迭代次数；如果随着迭代次数cost增加，那么选择更小的。

SGD一般不能得到全局最优，他会一直在最优值附近徘徊。学习率的大小一般保持不变，一个思路是可以动态的改变学习率的大小来提高准确度，比如随着迭代次数的增加慢慢减小的值。

14.2 Mini-Batch梯度下降

批量梯度下降：每次迭代都要用到所有的m个样本；

随机梯度下降：每次迭代只需要一个样本；

Mini-Batch梯度下降：每次迭代会使用b个样本，这里的b是一个成为Mini-Batch大小的参数。（将数据分为多份，对每一份执行GD，相当于GD和SGD的综合）

Mini-Batch梯度下降比随机梯度下降更快应该是因为取b个样本更能保证更新是沿着代价函数减小的方向。

14.3 在线学习机制

在线学习机制让我们可以模型化一些问题：有连续一波数据或连续的数据流想要用算法从中学习的这类问题。（大数据杀熟算法hhhh）

 

14.4 减少映射和数据并行

假设我们要训练一个线性回归模型或者是逻辑回归模型亦或其他模型。

 Map-reduce利用了线性回归求和运算的特性，将GD对整个数据的求和处理，分摊到多个服务器上执行，最后各个服务器把结果汇总到一起进行合并。

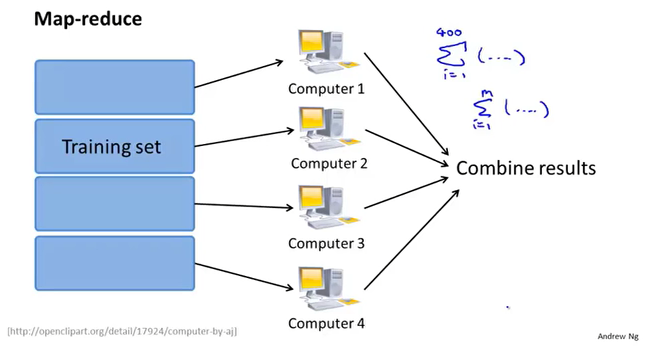
它和mini-batch应该是不一样的。mini-batch是对每b个样本迭代一次后更新参数，这个数据并行只是将数据切割成4份而已，更像是批量梯度下降的细分。

逻辑回归也可以这样