1. 视频链接
2. 数据集下载地址：无需下载

学习目标：

• 知道 XGBoost 算法原理
• 知道 otto 案例通过 XGBoost 实现流程
• 知道 LightGBM 算法原理
• 知道 PUBG 案例通过 LightGBM 实现流程
• 知道 Stacking 算法原理
• 知道住房月租金预测通过 Stacking 实现流程

1. XGBoost 算法原理

学习目标：

• 了解 XGBoost 的目标函数推导过程
• 知道 XGBoost 的回归树构建方法
• 知道 XGBoost 与 GDBT 的区别

---

XGBoost 是 Exterme Gradient Boosting（极限梯度提升）的缩写，XGBoost是集成学习方法的王牌，在 Kaggle 数据挖掘比赛中，大部分获胜者用了 XGBoost。

XGBoost 在绝大多数的回归和分类问题上表现的十分顶尖，本节将较详细的介绍 XGBoost 的算法原理。

1.1 最优模型的构建方法

我们在前面已经知道，构建最优模型的一般方法是最小化训练数据的损失函数。我们用字母 $L$ 表示损失，如下式：

$$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))\text{\hspace{1em}(1)}$$

其中：

• $L$ 表示损失函数
• $f$ 表示模型
• $F$ 表示模型的集合
  • $F$ 是假设空间（假设空间是在已知属性和属性可能取值的情况下，对所有可能满足目标的情况的一种毫无遗漏的假设集合）
• $N$ 表示训练数据的数量
• $y_i$ 表示第 $i$ 个数据的真实值
• $x_i$ 表示第 $i$ 个数据的特征值

在这个公式中，我们希望在假设空间 $F$ 中找到一个最优的模型 $f$，使得它能够最小化训练数据的平均损失。

$式(1)$ 称为经验风险最小化。因为训练得到的模型复杂度较高，而当训练数据较小时，模型很容易出现过拟合问题。因此为了降低模型的复杂度，常添加正则化（给模型惩罚使得模型变得简单），如下式所示：

$$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)\text{\hspace{1em}(2)}$$

其中：

• $\lambda$ 是一个正则化系数，它控制正则化项对损失函数的影响
• $J(f)$ 是一个正则化项，它用来衡量模型的复杂度。

这个公式表示我们希望在模型集合（假设空间）$F$ 中找到一个最优的模型 $f$，使得它能够最小化训练数据的平均损失和正则化项之和。

$式(2)$ 称为结构风险最小化。结构风险最小化的模型往往对训练数据以及未知的测试数据都有较好的预测。

---

应用：

• 决策树的生成和剪枝分别对应了经验风险最小化和结构风险最小化
• XGBoost 的决策树生成是结构风险最小化的结果，后续会详细介绍

1.2 XGBoost 的目标函数推导

1.2.1 目标函数确定

目标函数，即损失函数，我们一般通过最小化损失函数来构建最优模型。

由前面可知，损失函数应加上表示模型复杂度的正则项，且 XGBoost 对应的模型包含了多个 CART 树，因此，模型的目标函数为：

$$\mathrm{obj}(\theta )=\underset{\overline{模型的训练误差}}{\sum _{i=1}^{N}L(y_i,{\hat{y}}_i)}+\underset{\overline{所有\mathrm{CART}树的复杂度之和}}{\sum _{k=1}^K\Omega (f_k)}\text{\hspace{1em}(3-1)}$$

$式(3-1)$ 是正则化的损失函数。其中：

• $\mathrm{obj}(\theta )$ 表示目标函数
• $L$ 表示损失函数
• $N$ 表示训练数据的数量
• $y_i$ 表示第 $i$ 个数据的真实值
• ${\hat{y}}_i$ 表示第 $i$ 个数据的预测值
• $\Omega (f_k)$ 是第 $k$ 个 CART 树的复杂度
• $K$ 是 CART 树的数量。

这个公式表示我们希望最小化目标函数，即最小化训练数据的损失和所有 CART 树的复杂度之和。

1.2.2 CART 树的介绍

上图为第 $K$ 棵 CART 树，确定一棵 CART 树需要确定两部分：

• 第一部分就是树的结构。这个结构将输入样本 $X_i$ 映射到一个确定的叶子节点 $f_k$ 上，记为 $f_k(x)$
• 第二部分就是各个叶子节点的值 $w$。$q(x)$ 表示输出的叶子节点序号，$w_{q(x)}$ 表示对应叶子节点序号的值。

由定义得：

$$f_k(x)=w_{q(x)}\text{\hspace{1em}(3-2)}$$

1.2.3 树的复杂度定义

1.2.3.1 定义每棵树的复杂度

XGBoost 算法对应的模型包含了多棵 CART 树，定义每棵树的复杂度：

$$\Omega (f)=\gamma T+\frac{1}{2}\lambda ||w|{|}^2\text{\hspace{1em}(3-3)}$$

其中：

• $\gamma$ 和 $\lambda$ 是超参数
  • $\gamma$ 是树的复杂度参数，表示节点切分的难度
  • $\lambda$ 是 L2 正则化系数，用于控制模型的复杂度，避免过拟合
• $T$ 是树中叶子节点的个数
• $w$ 是叶子节点的得分值（叶子节点向量的模）

1.2.3.2 树的复杂度举例

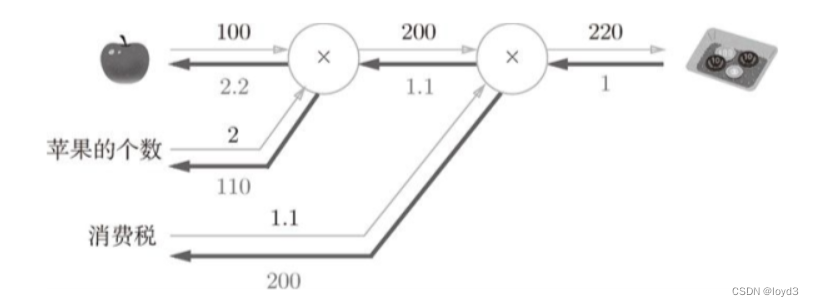
假设我们要预测一家人对电子游戏的喜好程度。考虑到年龄因素，年龄小的更可能喜欢电子游戏；考虑到性别因素，男性更喜欢电子游戏。故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给在电子游戏喜好程度上打分，如下图所示：

就这样，训练出了 2 棵树 tree1 和 tree2，类似之前 GBDT 的原理，两棵树的结论累加起来便是最终的结论，所以：

• 小男孩的预测分数就是两棵树中小孩所落到的结点的分数相加：$2+0.9=2.9$
• 爷爷的预测分数同理：$-1+(-0.9)=-1.9$

具体如下图所示：

树的复杂度求解如下图所示：

1.2.4 目标函数推导

根据 $式3-1$，共进行 $t$ 次迭代的学习模型的目标函数为：

$$\begin{array}{rl}{\mathrm{obj}}^{(t)}& =\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{(t)})+\sum _{k=1}^t\Omega (f_k)\\ & =\sum _{i=1}^{n}L(y_i,\underset{\overline{第t-1次}}{{\hat{y}}_i^{(t-1)}}+\underset{\overline{第t次}}{f_t(x_t)})+\underset{第t-1次}{\underline{\sum _{k=1}^{t-1}\Omega (f_k)}}+\underset{\overline{第t次}}{\Omega (f_t)}\end{array}\text{\hspace{1em}(4)}$$

由前向分布算法可知，前 $t-1$ 棵树的结构为常数：

$${\mathrm{obj}}^{(t)}==\sum _{i=1}^{n}L(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_t))+\Omega (f_t)+\mathrm{Constant}\text{\hspace{1em}(5)}$$

我们知道，泰勒公式的二阶导近似表示：

$$f(x_0+\Delta x)\approx f(x_0)+f^{\prime }(x_0)\cdot \Delta x+\frac{f^{\prime \prime }(x_0)}{2}\cdot \Delta x^2\text{\hspace{1em}(6)}$$

令 $f_t(x_i)$ 为 $\Delta x$，则 $式5$ 的二阶近似展开为：

$${\mathrm{obj}}^{(t)}\approx \sum _{i=1}^n\left[L(y_i,{\hat{y}}_i^{(t-1)})+g_i\cdot f_t(x_i)+\frac{1}{2}{h}_i\cdot f_t(x_i{)}^2\right]+\Omega (f_t)+\mathrm{Constant}\text{\hspace{1em}(7)}$$

$$\begin{array}{rl}& \because L(y_i,{\hat{y}}_i^{(t-1)})为常数\\ & \therefore {\mathrm{obj}}^{(t)}=\sum _{i=1}^n\left[g_i\cdot f_t(x_i)+\frac{1}{2}{h}_i\cdot f_t(x_i{)}^2\right]+\Omega (f_t)+\mathrm{Constant}\end{array}\text{\hspace{1em}(8)}$$

其中：

$$\begin{array}{rl}& g_i=\partial {\hat{y}}_{(t-1)}l(y_i,{\hat{y}}^{(t-1)})\\ & h_i={\partial }^2\hat{y}(t-1)l(y_i,{\hat{y}}^{(t-1)})\end{array}$$

其中：

• $g_i$ 和 $h_i$ 分别表示预测误差对当前模型的一阶导和二阶导
• $l(y_i,{\hat{y}}^{(t-1)})$ 表示前 $t-1$ 棵树组成的学习模型的预测误差

当前模型往预测误差减小的方向进行迭代。忽略 $式8$ 的常数项，并结合 $式4$，得：

$${\mathrm{obj}}^{(t)}=\sum _{i=1}^n\left[g_i\cdot f_t(x_i)+\frac{1}{2}{h}_i\cdot f_t(x_i{)}^2\right]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2\text{\hspace{1em}(9)}$$

通过 $式3-2$ 简化 $式9$：

$${\mathrm{obj}}^{(t)}=\underset{针对所有样本集求和}{\sum _{i=1}^n\left[g_i\cdot w_{q(x_i)}+\frac{1}{2}{h}_i\cdot w_{q(x_i)}^2\right]}+\gamma T+\underset{针对所有叶子节点求和}{\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2}\text{\hspace{1em}(10)}$$

$式10$ 第一部分是对所有训练样本集进行累加，此时所有样本都是映射为树的叶子节点。所以，我们换种思维，从叶子节点出发，对所有的叶子节点进行累加，得：

$${\mathrm{obj}}^{(t)}=\sum _{j=1}^T\left[(\sum _{i\in I_j}{g}_t)w_j+\frac{1}{2}(\sum _{i\in I_j}{h}_t+\lambda )w_j^2\right]+\gamma T\text{\hspace{1em}(11)}$$

其中：$T$ 代表叶子节点。

整体样本 $\in$ 叶子节点，叶子节点和样本属于一对多的关系。一些样本 $\in$ 某个叶子节点（某个叶子节点 包含 一个/多个 样本）

令 $$\sum _{i\in I_j}{g}_i=G_j,\sum _{i\in I_j}{h}_i=H_j$$

其中，$G_j$ 表示映射为叶子节点 $j$ 的所有输入样本的一阶导之和，同理，$H_j$ 表示二阶导之和。

得：

$${\mathrm{obj}}^{(t)}=\sum _{j=1}^T\left[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2\right]+\gamma T\text{\hspace{1em}(12)}$$

对于第 $t$ 棵 CART 树的某一个确定结构（可用 $q(x)$ 表示），其叶子节点是相互独立的，$G_j$ 和 $H_j$ 是确定量。因此，$式12$ 可以看成是关于叶子节点 $w$ 的一元二次函数。

最小化 $式12$ 得：

$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }\text{\hspace{1em}(13)}$$

把 $式13$ 带入到 $式12$，得到最终的目标函数：

$${\mathrm{obj}}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T\text{\hspace{1em}(14)}$$

$式14$ 也称为打分函数（Scoring Function），它是衡量树结构好坏的标准。

• ${\mathrm{obj}}^{\ast }$值越小，代表这样的结构越好。

我们用打分函数选择最佳切分点，从而构建 CART 树。

1.3 XGBoost 的回归树构建方法

1.3.1 计算分裂节点

在实际训练过程中，当建立第 $t$ 棵树时，XGBoost 采用贪心算法进行树结点的分裂：

从树深为 0 时开始：

• 对树中的每个叶子结点尝试进行分裂
• 每次分裂后，原来的一个叶子结点继续分裂为左右两个子叶子结点，原叶子结点中的样本集将根据该结点的判断规则分散到左右两个叶子结点中
• 新分裂一个结点后，我们需要检测这次分裂是否会给损失函数带来增益，增益的定义如下：$$\begin{array}{rl}\mathrm{Gain}& ={\mathrm{Obj}}_{L+R}-({\mathrm{Obj}}_L+{\mathrm{Obj}}_R)\\ & =\left[-\frac{1}{2}\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }+\gamma \right]-\left[-\frac{1}{2}\left(\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }\right)+2\gamma \right]\\ & =\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma \end{array}$$

如果增益 $\mathrm{Gain}>0$，即分裂为两个叶子节点后，目标函数下降了，那么我们会考虑此次分裂的结果。

那么一直这样分裂，什么时候才会停止呢？

1.3.2 停止分裂条件判断

情况一：增益为负

上节推导得到的打分函数是衡量树结构好坏的标准，因此，可用打分函数来选择最佳切分点。首先确定样本特征的所有切分点，对每一个确定的切分点进行切分，切分好坏的标准如下：

• $\mathrm{Gain}$ 表示单节点 $\mathrm{obj}$ 与切分后的两个节点的树 $\mathrm{obj}$ 之差，
• 遍历所有特征的切分点，找到最大 $\mathrm{Gain}$ 的切分点即是最佳分裂点，根据这种方法继续切分节点，得到 CART 树。
• 若 $\gamma$ 值设置的过大，则 $\mathrm{Gain}$ 为负，表示不切分该节点，因为切分后的树结构变差了。
  • $\gamma$ 值越大，表示对切分后 $\mathrm{obj}$ 下降幅度要求越严，这个值可以在 XGBoost 中设定。

简单来说，通过计算划分前和划分后Loss的大小，如果增益为正则继续分；如果增益为负则停止分。

情况二：达到树的最大深度

当树达到最大深度时，停止建树，因为树的深度太深容易出现过拟合，这里需要设置一个超参数 max_depth。

情况三：任意样本权重低于设定的阈值

当引入一次分裂后，重新计算新生成的左、右两个叶子结点的样本权重和。如果任一个叶子结点的样本权重低于某一个阈值，也会放弃此次分裂。这涉及到一个超参数：最小样本权重和。

该超参数是指，如果一个叶子节点包含的样本数量太少也会放弃分裂，防止树分的太细，这也是过拟合的一种措施。

1.4 XGBoost 与 GDBT 的区别

XGBoost 是一种高效的 Gradient Boosting 系统实现，而 GBDT 则特指梯度提升决策树算法。XGBoost 里面的基学习器除了用树（gbtree），也可以用线性分类器（gblinear）。在使用 CART 作为基分类器时，XGBoost 显式地加入了正则项 $\gamma$ 来控制模型的复杂度，有利于防止过拟合，从而提高模型的泛化能力。二者的区别有三点，如下所示：

1. 【区别一：树的复杂度】XGBoost 生成 CART 树考虑了树的复杂度；而 GDBT 未考虑树的复杂度（GDBT 在树的剪枝步骤中考虑了树的复杂度）。
2. 【区别二：损失函数展开】XGBoost 是拟合上一轮损失函数的二阶导展开，GDBT 是拟合上一轮损失函数的一阶导展开。因此，XGBoost 的准确性更高，且满足相同的训练效果时，需要的迭代次数更少。
3. 【区别三：运行速度】XGBoost 与GDBT都是逐次迭代来提高模型性能，但 XGBoost 在选取最佳切分点时可以开启多线程进行，大大提高了运行速度。

---

小结：

• XGBoost 的目标函数：$$\mathrm{obj}(\theta )=\sum _{i=1}^{n}L(y_i,{\hat{y}}_i)+\sum _{k=1}^K\Omega (f_k)$$
• 知道 XGBoost 的回归树构建方法$$\begin{array}{rl}\mathrm{Gain}& ={\mathrm{Obj}}_{L+R}-({\mathrm{Obj}}_L+{\mathrm{Obj}}_R)\\ & =\left[-\frac{1}{2}\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }+\gamma \right]-\left[-\frac{1}{2}\left(\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }\right)+2\gamma \right]\\ & =\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma \end{array}$$
• XGBoost 与 GDBT 的区别：
  1. 【区别一：树的复杂度】XGBoost 生成 CART 树考虑了树的复杂度；而 GDBT 未考虑树的复杂度（GDBT 在树的剪枝步骤中考虑了树的复杂度）。
  2. 【区别二：损失函数展开】XGBoost 是拟合上一轮损失函数的二阶导展开，GDBT 是拟合上一轮损失函数的一阶导展开。因此，XGBoost 的准确性更高，且满足相同的训练效果时，需要的迭代次数更少。
  3. 【区别三：运行速度】XGBoost 与GDBT都是逐次迭代来提高模型性能，但 XGBoost 在选取最佳切分点时可以开启多线程进行，大大提高了运行速度。

2. XGBoost 算法 API 介绍

学习目标：

• 了解 XGBoost 算法 API 中常用的参数

---

2.1 XGBoost 的安装

官网链接：[XGBoost Documentation](https:// XGBoost .readthedocs.io/en/latest/)

pip install  xgboost 

2.2 XGBoost 参数介绍

XGBoost 虽然被称为 Kaggle 比赛神器，但是我们要想训练出不错的模型，必须要给参数传递合适的值。

XGBoost 中封装了很多参数，主要由三种类型构成：通用参数（general parameters）、Booster 参数（booster parameters）以及学习目标参数（task parameters）。这三种参数的主要作用如下：

• 通用参数：主要是宏观函数控制
• booster 参数：取决于选择的 booster 类型，用于控制每一步的 booster（tree、regressiong）
• 学习目标参数：控制训练目标的表现

2.2.1 通用参数（general parameters）

XGBoost中的通用参数主要用于宏观函数控制。以下是一些常见的通用参数及其作用、默认值和可选值：

• booster [默认值=gbtree]：选择每次迭代的模型，有三种选择：
  • gbtree（基于树的模型）
  • dart（相比 gbtree，dart 主要多了 Dropout）
  • gblinear（线性模型）
• verbosity [默认值=1]：信息打印，0=silent、1=warning、2=info、3=debug。有时 XGBoost 会根据启发式来尝试修改配置，显示为 warning 信息。如果有意料之外的行为，可以尝试将 verbosity 的值增加。
• nthread [默认值为最大可能的线程数]：这个参数用来进行多线程控制，应当输入系统的核数。
  • 如果你希望使用CPU全部的核，那就不要输入这个参数，算法会自动检测它。
• disable_default_eval_metric [默认值=0]：是否禁用默认的评估指标，>0 表示禁用。
• num_pbuffer [自动设置，不需要用户设置]：预测缓冲区的大小，通常设置为训练实例的个数，缓冲区用来保存上次提升步骤的预测结果。
• num_feature [自动设置，不需用户设置]：设置为特征的最大维度。

2.2.2 Booster 参数（booster parameters）

XGBoost中的Booster参数用于控制每一步的booster（树或回归）。这里我们将其分为两类以分别介绍：

1. Tree Booster 参数
2. Linear Booster 参数

2.2.2.1 Tree Booster 参数

XGBoost 中的 Tree Booster 参数用于控制树模型。以下是一些常见的 Tree Booster 参数及其作用、默认值和可选值：

• eta [默认值=0.3，别名 Learning Rate]：与 GBM 中的 learning rate 参数类似，通过减少每一步的权重，可以提高模型的鲁棒性。典型值为 $0.01-0.2\in [0,1]$。
• gamma [默认值=0，别名 min_split_loss]：在节点分裂时，只有分裂后损失函数的值下降了，才会分裂这个节点。Gamma 指定了节点分裂所需的最小损失函数下降值。这个参数的值越大，算法越保守。取值范围为：$[0,+\infty ]$
• max_depth [默认值=6]：与 GBM 中的参数相同，这个值为树的最大深度。这个值也是用来避免过拟合的。max_depth 越大，模型会学到更具体更局部的样本。需要使用 CV 函数（交叉验证）来进行调优。典型值：$3-10\in [0,+\infty ]$。
• min_child_weight [默认值=1 $\in [0,+\infty ]$]：决定最小叶子节点样本权重和。这个参数用于避免过拟合。当它的值较大时，可以避免模型学习到局部的特殊样本。但是如果这个值过高，会导致欠拟合。这个参数需要使用 CV（交叉验证）来调整。
• subsample [默认值=1]：对训练集的二次抽样比例。
  • 将它设置为 0.5，表示 XGBoost 将首先抽取 50% 的样本来生成树，这将防止过拟合。每次提升迭代的过程中都将进行子抽样。
  • 减小这个参数的值，算法会更加保守，避免过拟合。但是，如果这个值设置得过小，它可能会导致欠拟合。
• colsample_bytree [默认值=1]：构建每个树时的子抽样比例。
• colsample_bylevel [默认值=1]：每层的列的子抽样比例。每一层抽样一次。从当前树中选出的列的集合中进行抽样。
• lambda [默认值=1，别名 reg_lambda]：权重的 L2 正则化项（和 Ridge Regression 类似），增加这个值会使模型更鲁棒。
  • 这个参数是用来控制 XGBoost 的正则化部分的。
  • 虽然大部分数据科学家很少用到这个参数，但是这个参数在减少过拟合上还是可以挖掘出更多用处的。
• alpha [默认值=0，别名 reg_alpha]：权重的 L1 正则化项（和Lasso Regression 类似）。可以应用在很高维度的情况下，使得算法的速度更快。
• scale_pos_weight [默认值=1]：控制正负权重的平衡，对于不平衡的类别是有用的。
  • 典型的值为：sum(negative instances) / sum(positive instances)。
  • 在各类别样本十分不平衡时，把这个参数设定为一个正值，可以使算法更快收敛。通常可以将其设置为负样本的数目与正样本数目的比值。

2.2.2.2 Linear Booster 参数

XGBoost中的Linear Booster参数用于控制线性模型。以下是一些常见的Linear Booster参数及其作用、默认值和可选值：

• lambda [缺省值 = 0，别称：reg_lambda]
  • L2 正则化惩罚系数，增加该值会使得模型更加保守。
• alpha [缺省值 = 0，别称：reg_alpha]
  • L1 正则化惩罚系数，增加该值会使得模型更加保守。
• lambda_bias [缺省值 = 0，别称：reg_lambda_bias]
  • 偏置上的 L2 正则化（没有在 L1 上加偏置，因为并不重要）

Linear Booster 用的很少。

2.2.3 学习目标参数（task parameters）

XGBoost中的学习目标参数（task parameters）用于指定学习任务和相应的学习目标。以下是一些常见的学习目标参数及其作用、默认值和可选值：

• objective [默认值=reg:squarederror]：指定学习任务和相应的学习目标。常用的可选参数值有：
  • “reg:squarederror”：线性回归。
  • “reg:logistic”：逻辑回归。
  • “binary:logistic”：二分类的逻辑回归问题，输出为概率。
  • “multi:softmax”：采用softmax函数处理多分类问题，返回预测的类别（不是概率）。同时需要设置参数num_class用于指定类别个数。
  • “multi:softprob”：与multi:softmax类似，但是输出的是每个数据属于各个类别的概率。
• eval_metric [默认值取决于objective参数]：用于指定评估指标。常用的评估指标有：
  • “rmse”：均方根误差，用于回归任务。
  • “mae”：平均绝对误差，用于回归任务。
  • “logloss”：负对数似然，用于二分类任务。
  • “error”：错误率，用于二分类任务。
  • “error@t”：不同的划分阈值可以通过 ‘t’ 进行设置
  • “merror”：多分类错误率，用于多分类任务。计算公式为 (wrong cases) / (all cases)
  • “mlogloss”：多分类负对数似然，用于多分类任务。
  • “auc”：曲线下面积，用于二分类任务。
• seed [默认值 = 0]：随机数种子。
  • 设置它可以复现随机数据的结果，也可以用于调整参数。

3. XGBoost 案例介绍

3.1 案例背景

该案例和前面 决策树 中所用案例一样。

泰坦尼克号沉没是历史上最臭名昭着的沉船之一。1912 年 4 月 15 日，在她的处女航中，泰坦尼克号在与冰山相撞后沉没，在 2224 名乘客和机组人员中造成 1502 人死亡。这场耸人听闻的悲剧震惊了国际社会，并为船舶制定了更好的安全规定。造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素，但有些人比其他人更容易生存，例如妇女，儿童和上流社会。

背景中提到的“在 2224 名乘客和机组人员中造成 1502 人死亡”这一数据并不准确。根据维基百科，泰坦尼克号上共有 2224 人，其中包括乘客和机组人员，而死亡人数在 1490-1635 人之间。

在这个案例中，我们要求完成对哪些人可能存活的分析。要求运用机器学习工具来预测哪些乘客幸免于悲剧。

案例：https://www.kaggle.com/c/titanic/overview

我们提取到的数据集中的特征包括票的类别，是否存活，乘坐班次，年龄，家庭住址/目的地，房间，船和性别等。

数据（目前无法访问）：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt
数据（可以访问，但有略微出入）：https://github.com/YBIFoundation/Dataset/blob/main/Titanic.txt

属性说明：

• pclass：客舱等级（1, 2, 3）
• survived：是否幸存（0, 1）
• name：姓名
• sex：性别
• age：年龄
• sibsp：船上兄弟姐妹/配偶的数量
• parch：船上父母/子女的数量
• ticket：船票号码
• fare：船票价格
• cabin：客舱号码
• embarked：登船港口
• boat：救生艇编号
• body：遗体识别号码
• home.dest：家庭住址/目的地

经过观察数据得到：

• pclass：客舱等级（1, 2, 3）是社会经济阶层的代表
• 其中 age 数据存在缺失

3.2 步骤分析

1. 获取数据
2. 数据基本处理
   1. 确定特征值、目标值
   2. 缺失值处理
   3. 数据集划分
3. 特征工程（字典特征抽取）
4. 机器学习（XGBoost）
5. 模型评估

3.3 代码实现

导入需要的库：

import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split

一、获取数据

titanic = pd.read_csv("./data/titanic.txt")

二、数据基本处理

二·一、确定特征值、目标值

# 我们需要将列名放在一个列表中
x = titanic[["pclass", "age", "sex"]].copy()
y = titanic["survived"].copy()

二·二、缺失值处理

# 缺失值需要处理，将特征当值有类别的这些特征进行字典特征抽取
x.loc[:, "age"].fillna(x["age"].mean(), inplace=True)

二·三、数据集划分

x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)

三、特征工程

特征中出现类别符号，需要进行 one-hot 编码处理（DictVectorizer）

x.to_dict(orient="records") 需要将数组特征转换成字典数据。

# 对于 x 转换成字典数据 x.to_dict(orient="records")
transfer = DictVectorizer(sparse=False)

x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.transform(x_test.to_dict(orient="records"))  # 别用fit_transform了

四、XGBoost 模型训练

# 模型初步训练
from xgboost import XGBClassifier
xgb = XGBClassifier()

xgb.fit(x_train, y_train)

五、模型评估

score = xgb.score(x_test, y_test)
print(f"模型准确率为：{score*100:.4f}%")

模型准确率为：77.7439%

六、模型调优

depth_range = range(1, 11)
scores = []

for i in depth_range:
    xgb = XGBClassifier(eta=1, gamma=0, max_depth=i)
    xgb.fit(x_train, y_train)
    
    acc = xgb.score(x_test, y_test)
    print(f"max_depth = {i} 时，模型准确率为：{acc * 100:.4f}%")
    scores.append(acc)

print(scores)
print(f"\r\n模型准确率最高为：{max(scores) * 100:.4f}%，此时 max_depth = {depth_range[np.argmax(scores)]} ")

max_depth = 1 时，模型准确率为：76.2195%
max_depth = 2 时，模型准确率为：76.8293%
max_depth = 3 时，模型准确率为：77.7439%
max_depth = 4 时，模型准确率为：75.6098%
max_depth = 5 时，模型准确率为：76.2195%
max_depth = 6 时，模型准确率为：75.0000%
max_depth = 7 时，模型准确率为：74.0854%
max_depth = 8 时，模型准确率为：76.5244%
max_depth = 9 时，模型准确率为：75.9146%
max_depth = 10 时，模型准确率为：76.5244%
[0.7621951219512195, 0.7682926829268293, 0.7774390243902439, 0.7560975609756098, 0.7621951219512195, 0.75, 0.7408536585365854, 0.7652439024390244, 0.7591463414634146, 0.7652439024390244]

模型准确率最高为：77.7439%，此时 max_depth = 3 

七、调优结果可视化

import matplotlib.pyplot as plt


plt.figure(dpi=300)
plt.scatter(depth_range, scores)
plt.plot(depth_range, scores)
plt.show()

4. otto 案例【XGBoost 实现】：Otto Group Product Classification Challenge

4.1 otto（Otto Group Product Classification Challenge）案例介绍

奥托集团是世界上最大的电子商务公司之一，在 20 多个国家设有子公司。该公司每天都在世界各地销售数百万种产品，所以对其产品根据性能合理的分类非常重要。

不过，在实际工作中，工作人员发现许多相同的产品得到了不同的分类。本案例要求你对奥拓集团的产品进行正确的分分类。尽可能的提供分类的准确性。

链接：Otto Group Product Classification Challenge

对于这次比赛，我们提供了一个包含超过200,000种产品的93个特征的数据集。目标是建立一个预测模型，能够区分我们的主要产品类别。

4.2 数据集介绍

本案例中，数据集包含大约 200,000 种产品的 93 个特征。其目的是建立一个能够区分 otto 公司主要产品类别的预测模型。所有产品共被分成九个类别（例如时装，电子产品等）。

其中：

• id：产品ID
• feat_1, feat_2, ..., feat_93：产品的各个特征
• target：产品被划分的类别

4.3 评分标准

本案例中，最后结果使用多分类对数损失进行评估。具体公式为：

$$\log \mathrm{loss}=-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^M{y}_{ij}\log (p_{ij})$$

其中：

• $i$ 表示样本
• $j$ 表示类别
• $p_{ij}$ 代表第 $i$ 个样本属于类别 $j$ 的概率
• 如果第 $i$ 个样本真的属于类别 $j$，则 $y_{ij}$ 等于1，否则为0

根据上公式，假如模型将所有的测试样本都正确分类，即所有 $p_{ij}$ 都是1，那每个 $\log (p_{ij})$ 都是0，最终的 $\log \mathrm{loss}(p_{ij})$ 也是0。

假如第 1 个样本本来是属于 1 类别的，但模型给它的类别概率 $p_{ij}=0.1$，那 $\log \mathrm{loss}$ 就会累加上 $\log (0.1)$ 这一项。我们知道这一项是负数，而且 $p_{ij}$ 越小，负得越多，如果 $p_{ij}=0$，将是无穷。这会导致这种情况：模型分错了一个，$\log \mathrm{loss}$ 就是无穷。这当然不合理，为了避免这一情况，我们对非常小的值做如下处理：

$$\max (\min (p,1-10^{-15}),10^{-15})$$

也就是说，最小不会小于 $10^{-15}$。

4.4 思路分析

1. 获取数据
2. 数据基本处理
   1. 数据量比较大，截取部分数据
   2. 转换目标值表示方式（转换为数字）
   3. 分割数据（使用 StratifiedShuffleSplit）
   4. 数据标准化
   5. 数据 PCA 降维
3. 模型训练和模型评估
   1. 基本模型训练
   2. 模型调优
      1. 调优参数：
         1. n_estimator：指模型中树的数量。增加树的数量可以提高模型的复杂度，但也可能导致过拟合。
         2. max_depth：指每棵树的最大深度。增加树的深度可以提高模型的复杂度，但也可能导致过拟合。
         3. min_child_weights：指子节点中所需的最小样本权重和。这个参数用于控制树的生长，较大的值可以防止过拟合，但也可能导致欠拟合。
         4. subsamples：指用于训练每棵树的样本比例。较小的值可以防止过拟合，但也可能导致欠拟合。
         5. consample_bytrees：指用于训练每棵树的特征比例。较小的值可以防止过拟合，但也可能导致欠拟合。
         6. etas：指学习率，用于控制每棵树对最终预测结果的贡献。较小的值可以防止过拟合，但会增加训练时间。
   3. 确定最优参数

4.5 代码实现

之前在 [学习笔记] [机器学习] 7. 集成学习（Bagging、随机森林、Boosting、GBDT） 中写过重复代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


# 1. 获取数据
data = pd.read_csv("./data/otto-group-product-classification-challenge/train.csv")

# 2. 数据基本处理

## 2.1 截取部分数据
new_data = data[:10000]

# 随机欠采样获取部分数据集
## 首先需要确定标签值
y = data["target"]
x = data.drop(["id", "target"], axis=1)

## 欠采样获取数据
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
x_resampled, y_resampled = rus.fit_resample(x, y)

## 2.2 把目标值转换为数字
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y_resampled = le.fit_transform(y_resampled)

二·三、分割数据

from sklearn.model_selection import StratifiedShuffleSplit

sss = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=0)
for train_idx, test_idx in sss.split(x_resampled.values, y_resampled):
    print(len(train_idx))
    print(len(test_idx))
    
    x_train = x_resampled.values[train_idx]
    x_test = x_resampled.values[test_idx]
    
    y_train = y_resampled[train_idx]
    y_test = y_resampled[test_idx]

# 分割数据可视化
import seaborn as sns


plt.figure(dpi=300)
sns.countplot(x=y_test)
plt.show()

二·四、数据标准化

from sklearn.preprocessing import StandardScaler


scaler = StandardScaler()
scaler.fit(x_train)

x_train_scaled = scaler.transform(x_train)
x_test_scaled = scaler.transform(x_test)

二·五、数据 PCA 降维

from sklearn.decomposition import PCA


pca = PCA(n_components=0.9)  # 保留90%的特征
x_train_pca = pca.fit_transform(x_train_scaled)
x_test_pca = pca.transform(x_test_scaled)

print("降维前数据的形状为：", x_train_scaled.shape, x_test_scaled.shape)
print("降维后数据的形状为：", x_train_pca.shape, x_test_pca.shape)

降维前数据的形状为： (13888, 93) (3473, 93)
降维后数据的形状为： (13888, 65) (3473, 65)

从上面输出的数据可以看出，通过 PCA 降维，我们只选择 65 个特征就可以表达出原来 90% 的特征信息。

import matplotlib.pyplot as plt
from pylab import mpl
# 设置中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False


plt.figure(dpi=300)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel("特征数量")
plt.ylabel("可表达信息的百分比")
plt.show()

其中：

1. pca.explained_variance_ratio_ 是 PCA（主成分分析）对象的一个属性，它表示每个主成分所解释的方差比例。
   PCA 是一种常用的降维方法，它通过将数据投影到由主成分构成的新坐标系中，来实现降维。每个主成分都是原始数据中方差最大的方向。
   pca.explained_variance_ratio_ 属性返回一个数组，其中第 i 个元素表示第 i 个主成分所解释的方差比例。这些比例之和为 1。
   例如，如果 pca.explained_variance_ratio_ 返回 [0.6, 0.3, 0.1]，则表示第一个主成分解释了原始数据中 60% 的方差，第二个主成分解释了 30% 的方差，第三个主成分解释了 10% 的方差。
   我们可以使用 pca.explained_variance_ratio_ 来确定保留多少个主成分。通常，我们会选择保留足够多的主成分，使得它们能够解释原始数据中大部分的方差。
2. np.cumsum 是 NumPy 库中的一个函数，它用于计算给定数组的累积和。
   累积和是指将数组中每个元素与它前面所有元素的和依次累加起来。例如，对于一维数组 [1, 2, 3, 4]，它的累积和为 [1, 3, 6, 10]。
   下面是一个使用 np.cumsum 计算一维数组累积和的示例：

   import numpy as np
   arr = np.array([1, 2, 3, 4])
   cumsum = np.cumsum(arr)
   print(cumsum)
   

   输出结果为：

   [ 1  3  6 10]
   

   np.cumsum 还可以用于计算多维数组的累积和。我们还可以通过指定 axis 参数来控制沿哪个轴进行累积求和。

三、模型训练和模型评估

三·一、基本模型训练

from xgboost import XGBClassifier


xgb = XGBClassifier()
xgb.fit(x_train_pca, y_train)

# 改变预测值的输出模式，让输出结果为百分占比，降低Log Loss值
y_pred_proba = xgb.predict_proba(x_test_pca)

# Log Loss进行模型评估
from sklearn.metrics import log_loss
loss = log_loss(y_test, y_pred_proba, eps=1e-15, normalize=True)
print(f"Log Loss 值为：{loss}")
print(f"XGBoost模型参数为：\r\n{xgb.get_params}")

Log Loss 值为：0.7358510025107224

XGBoost模型参数为：
<bound method XGBModel.get_params of XGBClassifier(base_score=None, booster=None, callbacks=None,
              colsample_bylevel=None, colsample_bynode=None,
              colsample_bytree=None, early_stopping_rounds=None,
              enable_categorical=False, eval_metric=None, feature_types=None,
              gamma=None, gpu_id=None, grow_policy=None, importance_type=None,
              interaction_constraints=None, learning_rate=None, max_bin=None,
              max_cat_threshold=None, max_cat_to_onehot=None,
              max_delta_step=None, max_depth=None, max_leaves=None,
              min_child_weight=None, missing=nan, monotone_constraints=None,
              n_estimators=100, n_jobs=None, num_parallel_tree=None,
              objective='multi:softprob', predictor=None, ...)>

三·二、模型调优

训练起来可能速度比较慢（取决于计算机 CPU 性能）
为了加速计算，我使用了 GPU 😄

三·二·一、n_estimators

n_estimator：指模型中树的数量。增加树的数量可以提高模型的复杂度，但也可能导致过拟合。

# 1. n_estimators：指模型中树的数量。增加树的数量可以提高模型的复杂度，但也可能导致过拟合。
losses = []
n_estimators_lst = [100, 200, 400, 450, 500, 550, 600, 700]

for n in n_estimators_lst:
    xgb = XGBClassifier(max_depth = 3, 
                        learning_rate = 0.1,
                        n_estimators = n,
                        objective = "multi:softprob",
                        n_jobs = -1,
                        nthread = 4,
                        min_child_weight = 1,
                        subsample = 1,
                        colsample_bytree = 1,
                        tree_method='gpu_hist',
                        seed = 42)
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[n_estimator = {n}] 测试集的 Log Loss 值为：{loss}")

[n_estimator = 100] 测试集的 Log Loss 值为：0.7848766538559263
[n_estimator = 200] 测试集的 Log Loss 值为：0.7170554363441936
[n_estimator = 400] 测试集的 Log Loss 值为：0.6825742112662687
[n_estimator = 450] 测试集的 Log Loss 值为：0.6799066727133629
[n_estimator = 500] 测试集的 Log Loss 值为：0.677094973209725
[n_estimator = 550] 测试集的 Log Loss 值为：0.6764860324507066
[n_estimator = 600] 测试集的 Log Loss 值为：0.6770196909007524
[n_estimator = 700] 测试集的 Log Loss 值为：0.6786069169388445

# 模型LogLoss可视化
best_pt_x = n_estimators_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(n_estimators_lst, losses)
plt.plot(n_estimators_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("n_estimator")
print(f"n_estimators的最优值为：{best_pt_x}")

n_estimators的最优值为：550

三·二·二、max_depth

max_depth：指每棵树的最大深度。增加树的深度可以提高模型的复杂度，但也可能导致过拟合。

# 1. max_depth：指每棵树的最大深度。增加树的深度可以提高模型的复杂度，但也可能导致过拟合。
losses = []
max_depth_lst = [1, 3, 5, 6, 7]

for depth in n_estimators_lst:
    xgb = XGBClassifier(max_depth = depth, 
                        learning_rate = 0.1,
                        n_estimators = 550,
                        objective = "multi:softprob",
                        n_jobs = -1,
                        nthread = 4,
                        min_child_weight = 1,
                        subsample = 1,
                        colsample_bytree = 1,
                        seed = 42)
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[max_depth = {depth}] 测试集的 Log Loss 值为：{loss}")

# 2. max_depth：指每棵树的最大深度。增加树的深度可以提高模型的复杂度，但也可能导致过拟合。
losses = []
max_depth_lst = [1, 3, 5, 6, 7]

for depth in max_depth_lst:
    xgb = XGBClassifier(max_depth = depth, 
                        learning_rate = 0.1,
                        n_estimators = 550,
                        objective = "multi:softprob",
                        n_jobs = -1,
                        nthread = 4,
                        min_child_weight = 1,
                        subsample = 1,
                        colsample_bytree = 1,
                        seed = 42)
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[max_depth = {depth}] 测试集的 Log Loss 值为：{loss}")

[max_depth = 1] 测试集的 Log Loss 值为：0.8179933385612383
[max_depth = 3] 测试集的 Log Loss 值为：0.6728414311785795
[max_depth = 5] 测试集的 Log Loss 值为：0.7328000228260207
[max_depth = 6] 测试集的 Log Loss 值为：0.767504664266815
[max_depth = 7] 测试集的 Log Loss 值为：0.7780594028272297

# 模型LogLoss可视化
best_pt_x = max_depth_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(max_depth_lst, losses)
plt.plot(max_depth_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("max_depth_lst")
print(f"max_depth 的最优值为：{best_pt_x}")

max_depth 的最优值为：3

三·二·三、min_child_weights

min_child_weights：指子节点中所需的最小样本权重和。这个参数用于控制树的生长，较大的值可以防止过拟合，但也可能导致欠拟合。

# 3. min_child_weights：指子节点中所需的最小样本权重和。这个参数用于控制树的生长，较大的值可以防止过拟合，但也可能导致欠拟合。
losses = []
min_child_weights_lst = [1, 3, 5, 6, 7]

for mcw in min_child_weights_lst:
    xgb = XGBClassifier(max_depth=3,
                        learning_rate=0.1,
                        n_estimators=550,
                        objective="multi:softprob",
                        n_jobs=-1,
                        nthread=4,
                        min_child_weight=mcw,
                        subsample=1,
                        colsample_bytree=1,
                        seed=42,
                        tree_method='gpu_hist')  # 指定使用 GPU
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[min_child_weights = {mcw}] 测试集的 Log Loss 值为：{loss}")

[min_child_weights = 1] 测试集的 Log Loss 值为：0.6728414311785795
[min_child_weights = 3] 测试集的 Log Loss 值为：0.6692908565537544
[min_child_weights = 5] 测试集的 Log Loss 值为：0.6706406067281007
[min_child_weights = 6] 测试集的 Log Loss 值为：0.6747879047090067
[min_child_weights = 7] 测试集的 Log Loss 值为：0.6726420132442011

# 模型LogLoss可视化
best_pt_x = min_child_weights_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(min_child_weights_lst, losses)
plt.plot(min_child_weights_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("min_child_weights")
print(f"min_child_weights 的最优值为：{best_pt_x}")

min_child_weights 的最优值为：3

三·二·四、subsamples

subsamples：指用于训练每棵树的样本比例。较小的值可以防止过拟合，但也可能导致欠拟合。

# 4. subsamples：指用于训练每棵树的样本比例。较小的值可以防止过拟合，但也可能导致欠拟合。
losses = []
subsamples_lst = np.linspace(start=0.1, stop=1.0, num=10)

for ss in subsamples_lst:
    xgb = XGBClassifier(max_depth=3,
                        learning_rate=0.1,
                        n_estimators=550,
                        objective="multi:softprob",
                        n_jobs=-1,
                        nthread=4,
                        min_child_weight=3,
                        subsample=ss,
                        colsample_bytree=1,
                        seed=42,
                        tree_method='gpu_hist')  # 指定使用 GPU
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[subsamples = {ss}] 测试集的 Log Loss 值为：{loss}")
    
    
# 模型LogLoss可视化
best_pt_x = subsamples_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(subsamples_lst, losses)
plt.plot(subsamples_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("subsamples")
print(f"subsamples 的最优值为：{best_pt_x}")

[subsamples = 0.1] 测试集的 Log Loss 值为：0.7182164104154481
[subsamples = 0.2] 测试集的 Log Loss 值为：0.6779277134981072
[subsamples = 0.3] 测试集的 Log Loss 值为：0.6828323743996116
[subsamples = 0.4] 测试集的 Log Loss 值为：0.681844705484641
[subsamples = 0.5] 测试集的 Log Loss 值为：0.6658174785559277
[subsamples = 0.6] 测试集的 Log Loss 值为：0.6645719932485671
[subsamples = 0.7] 测试集的 Log Loss 值为：0.6608297840206926
[subsamples = 0.8] 测试集的 Log Loss 值为：0.6639568070272038
[subsamples = 0.9] 测试集的 Log Loss 值为：0.6624098487915533
[subsamples = 1.0] 测试集的 Log Loss 值为：0.6692908565537544

subsamples 的最优值为：0.7

三·二·五、consample_bytrees

consample_bytrees：指用于训练每棵树的特征比例。较小的值可以防止过拟合，但也可能导致欠拟合。

# 5. consample_bytrees：指用于训练每棵树的特征比例。较小的值可以防止过拟合，但也可能导致欠拟合。
losses = []
consample_bytrees_lst = np.round(np.linspace(start=0.1, stop=1.0, num=10), 1)

for csbt in consample_bytrees_lst:
    xgb = XGBClassifier(max_depth=3,
                        learning_rate=0.1,
                        n_estimators=550,
                        objective="multi:softprob",
                        n_jobs=-1,
                        nthread=4,
                        min_child_weight=3,
                        subsample=0.7,
                        colsample_bytree=csbt,
                        seed=42,
                        tree_method='gpu_hist')  # 指定使用 GPU
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[subsamples = {csbt}] 测试集的 Log Loss 值为：{loss}")
    
    
# 模型LogLoss可视化
best_pt_x = consample_bytrees_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(consample_bytrees_lst, losses)
plt.plot(consample_bytrees_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("consample_bytrees")
print(f"consample_bytrees 的最优值为：{best_pt_x}")

[subsamples = 0.1] 测试集的 Log Loss 值为：0.6888312639423317
[subsamples = 0.2] 测试集的 Log Loss 值为：0.6666403661429002
[subsamples = 0.3] 测试集的 Log Loss 值为：0.6679597840226225
[subsamples = 0.4] 测试集的 Log Loss 值为：0.6617385267686424
[subsamples = 0.5] 测试集的 Log Loss 值为：0.6628833643901699
[subsamples = 0.6] 测试集的 Log Loss 值为：0.6650225867566126
[subsamples = 0.7] 测试集的 Log Loss 值为：0.6592889672292022
[subsamples = 0.8] 测试集的 Log Loss 值为：0.6633614798476566
[subsamples = 0.9] 测试集的 Log Loss 值为：0.6604106249169214
[subsamples = 1.0] 测试集的 Log Loss 值为：0.6608297840206926

consample_bytrees 的最优值为：0.7

三·二·六、etas

etas：指学习率，用于控制每棵树对最终预测结果的贡献。较小的值可以防止过拟合，但会增加训练时间。

# 6. etas：指学习率，用于控制每棵树对最终预测结果的贡献。较小的值可以防止过拟合，但会增加训练时间。
losses = []
etas_lst = [0.001, 0.01, 0.05, 0.07, 0.08, 0.1, 0.15, 0.20, 0.5, 0.7, 0.9, 1.0]

for lr in etas_lst:
    xgb = XGBClassifier(max_depth=3,
                        learning_rate=lr,
                        n_estimators=550,
                        objective="multi:softprob",
                        n_jobs=-1,
                        nthread=4,
                        min_child_weight=3,
                        subsample=0.7,
                        colsample_bytree=0.7,
                        seed=42,
                        tree_method='gpu_hist')  # 指定使用 GPU
    xgb.fit(x_train_pca, y_train)
    y_pred = xgb.predict_proba(x_test_pca)
    loss = log_loss(y_test, y_pred)
    losses.append(loss)
    print(f"[etas = {lr:.3f}] 测试集的 Log Loss 值为：{loss}")
    
    
# 模型LogLoss可视化
best_pt_x = etas_lst[np.argmin(losses)]
best_pt_y = np.min(losses)

plt.figure(dpi=300)
plt.scatter(etas_lst, losses)
plt.plot(etas_lst, losses)
plt.scatter(best_pt_x, best_pt_y, c="red", zorder=10)
plt.ylabel("Log Loss")
plt.xlabel("etas(Learning Rate)")
print(f"etas（Learning Rate） 的最优值为：{best_pt_x}")

[etas = 0.001] 测试集的 Log Loss 值为：1.7032787119265516
[etas = 0.010] 测试集的 Log Loss 值为：0.8833413617350854
[etas = 0.050] 测试集的 Log Loss 值为：0.6800088492909538
[etas = 0.070] 测试集的 Log Loss 值为：0.6666148796577162
[etas = 0.080] 测试集的 Log Loss 值为：0.6629036617412906
[etas = 0.100] 测试集的 Log Loss 值为：0.6592889672292022
[etas = 0.150] 测试集的 Log Loss 值为：0.6769270295637069
[etas = 0.200] 测试集的 Log Loss 值为：0.7025856522466983
[etas = 0.500] 测试集的 Log Loss 值为：0.8732219186357921
[etas = 0.700] 测试集的 Log Loss 值为：1.0123982294813048
[etas = 0.900] 测试集的 Log Loss 值为：1.0930137685114494
[etas = 1.000] 测试集的 Log Loss 值为：1.149427276501444

etas（Learning Rate） 的最优值为：0.1

三·三、确定最优模型参数

# 最优模型参数
xgb = XGBClassifier(max_depth=3,
                    learning_rate=0.1,
                    n_estimators=550,
                    objective="multi:softprob",
                    n_jobs=-1,
                    nthread=4,
                    min_child_weight=3,
                    subsample=0.7,
                    colsample_bytree=0.7,
                    seed=42,
                    tree_method='gpu_hist')  # 指定使用 GPU
xgb.fit(x_train_pca, y_train)
y_pred = xgb.predict_proba(x_test_pca)
loss = log_loss(y_test, y_pred)
losses.append(loss)
print(f"测试集的 Log Loss 值为：{loss}")

测试集的 Log Loss 值为：0.6592889672292022

5. LightGBM 算法原理

学习目标：

• 了解 LightGBM 演进过程
• 知道什么是 LightGBM
• 知道 LightGBM 原理

5.1 前言

5.1.1 LightGBM 演进过程

$$\begin{array}{rl}& C3.0(信息增益,信息增益率)\to \mathrm{CART}(\mathrm{Gini})\to 提升树(\mathrm{AdaBoost})\\ & \to \mathrm{GBDT}\to \mathrm{XGBoost}\to \mathrm{LightGBM}\end{array}$$

其中：

• 公式中的字符代表不同的算法及其决策树分裂的相应标准
  • C3.0 使用信息增益和增益率
  • CART 使用基尼指数
  • AdaBoost 是一种可以与决策树一起使用的提升算法
  • GBDT 代表梯度提升决策树
  • XGBoost 代表极端梯度提升
  • LightGBM 代表轻量级梯度提升机

5.1.2 AdaBoost 算法

AdaBoost 是一种提升树的方法，和三个臭裨将顶个诸葛亮的道理一样。

AdaBoost 有两个问题：

1. [样本数据权重] 如何改变训练数据的权重或概率分布？
   A：提高前一轮被弱分类器错误分类的样本的权重，降低前一轮被分对的权重
2. [分类器权重] 如何将弱分类器组合成一个强分类器：对于每个分类器，前面的权重如何设置？
   A：采取“多数表决”的方法，加大分类错误率小的弱分类器的权重，使其作用较大；同时减小分类错误率大的弱分类器的权重，使其在表决中起较小的作用。

5.1.3 GBDT 算法以及优缺点

GBDT 和 AdaBosst 很类似，但是又有所不同。

• GBDT 和其它 Boosting 算法一样，通过将表现一般的几个模型（通常是深度固定的决策树）组合在一起来集成一个表现较好的模型。
• AdaBoost 提升树是通过提升错分数据点的权重来定位模型的不足。
• Gradient Boosting Decision Tree（GBDT）则是通过负梯度来识别问题，通过计算负梯度来改进模型，即通过反复地选择一个指向负梯度方向的函数，该算法可被看做在函数空间里对目标函数进行优化。

因此可以说：

$$\mathrm{Gradient}\mathrm{Boosting}\mathrm{Decision}\mathrm{Tree}(\mathrm{GBDT})=\mathrm{Gradient}\mathrm{Descent}+\mathrm{Boosting}$$

---

缺点：

因为 GBDT 是基于预排序方法（pre-sorted）构建的，所以存在一些问题：

1. 空间消耗大
   这样的算法不仅需要保存数据的特征值，还需要保存特征排序的结果（例如排序后的索引，为了后续快速的计算分割点），这里需要消耗训练数据两倍的内存。
2. 运算时间长
   在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的时间较多。
3. 对内存（cache）优化不友好
   在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对 cache 进行优化。
   同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的 cache miss。

Cache miss是指当一个组件或应用程序请求处理数据时，在缓存内存中找不到该数据的状态。这会导致执行延迟，因为程序或应用程序需要从其他缓存级别或主内存中获取数据。

5.1.4 启发

常用的机器学习算法，例如神经网络等算法，都可以以 mini-batch 的方式训练，训练数据的大小不会受到内存限制。而 GBDT 在每一次迭代的时候，都需要遍历整个训练数据多次。

• 如果把整个训练数据装进内存，则会限制训练数据的大小；
• 如果不装进内存，反复地读写训练数据又会消耗非常大的时间。

尤其是面对工业级海量的数据，普通的 GBDT 算法是不能满足其需求的（又耗时又费内存）。LightGBM 提出的主要原因就是为了解决 GBDT 在海量数据遇到的问题，让 GBDT 可以更好更快地用于工业实践。

5.2 什么是 LightGBM

LightGBM 的全拼是 Light Gradient Boosting Machine，中文名称是轻量级梯度提升机。LightGBM 是 2017 年 1 月，微软在 GitHub 上开源的一个新的梯度提升框架。

GitHub：LightGBM

在开源之后，就被别人冠以“速度惊人”“支持分布式”“代码清晰易懂”“占用内存小”等属性。LightGBM 主打的高效并行训练让其性能超越现有其他 Boosting 工具。在 HIGGS 数据集上的试验表明，LightGBM 比 XGBoost 快将近 10 倍，内存占用率大约为 XGBoost 的 1/6。

HIGGS数据集是一个分类问题，用于区分产生希格斯玻色子的信号过程和不产生希格斯玻色子的背景过程。该数据集使用蒙特卡洛模拟生成。前 21 个特征（第 2-22 列）是加速器中粒子探测器测量的运动学性质。后七个特征是前 21 个特征的函数；这些是物理学家推导出来的高级特征，用于帮助区分两个类别。人们对使用深度学习方法来避免物理学家手动开发这些特征感兴趣。原始论文中介绍了使用标准物理软件包中的贝叶斯决策树和 5 层神经网络的基准结果。

数据集下载地址：HIGGS

5.3 LightGBM 原理

LightGBM是一种梯度提升决策树算法，它通过以下几种方式进行优化和提升性能：

1. 基于直方图（Histogram）的决策树算法：LightGBM 使用基于直方图的算法来构建决策树，这种方法可以减少内存占用并加快计算速度。
2. LightGBM的直方图做差加速：LightGBM 使用一种称为直方图做差的技术来进一步加快计算速度。这种方法通过重复利用父节点的直方图来计算子节点的直方图，从而避免了对整个数据集的扫描。
3. 带深度限制的Leaf-wise的叶子生长策略：LightGBM 使用一种称为 Leaf-wise 的叶子生长策略来构建决策树。这种方法在每次分裂时选择具有最大增益的叶子节点进行分裂，而不是按层分裂。这种方法可以更快地降低损失，但也可能导致过拟合。因此，LightGBM 引入了深度限制来控制树的生长。
4. 直接支持类别特征：LightGBM 可以直接处理类别特征，而无需进行独热编码。这可以减少内存占用并加快计算速度。
5. 直接支持高效并行：LightGBM 支持高效的并行训练，可以在多个 CPU 核心或多个机器上同时训练模型，从而进一步提高训练速度。

Histogram：英[ˈhɪstəɡræm] 美[ˈhɪstəɡræm]
n. 直方图; （统计学的）直方图，矩形图;

具体解释见下，分节介绍。

5.3.1 基于 Histogram（直方图）的决策树算法

直方图算法的基本思想是：

• 先把连续的浮点特征值离散化成 $k$ 个整数，同时构造一个宽度为 $k$ 的直方图。
• 在遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量。当遍历一次数据后，直方图累积了需要的统计量；然后根据直方图的离散值，遍历寻找最优的分割点。

举例：

[0, 0.1] -> 0;
[0.1, 0.3] -> 1;
...

例子中，将浮点值离散化为整数。例如，浮点值在 $[0,0.1]$ 范围内的值将被映射到整数 0，而浮点值在 $[0.1,0.3]$ 范围内的值将被映射到整数 1。

使用直方图算法有很多优点。首先，最明显就是内存消耗的降低。直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用 8 位整型（int）存储就足够了，内存消耗可以降低为原来的 1/8。

然后在计算上代价也大幅降低，预排序算法每遍历一个特征值就需要计算一次分裂的增益，而直方图算法只需要计算 $k$ 次（$k$ 可以认为是常数），时间复杂度从 $O(\mathrm{data}\times \mathrm{feature})$ 优化到 $O(k\times \mathrm{features})$。

当然，Histogram 算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。但在不同的数据集上的结果表明，离散化的分割点对最终的精度影响并不是很大，甚至有时候会更好一点。原因是决策树本来就是弱模型，分割点是不是精确并不是太重要；较粗的分割点也有正则化的效果，可以有效地防止过拟合；即使单棵树的训练误差比精确分割的算法稍大，但在梯度提升（Gradient Boosting）的框架下没有太大的影响。

和 混合精度 的表现差不多

5.3.2 LightGBM的 Histogram（直方图）做差加速

一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。

通常构造直方图，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的 $k$ 个桶（bucket）。利用这个方法，LightGBM 可以在构造一个叶子的直方图后，可以用非常微小的代价得到它兄弟叶子的直方图，在速度上可以提升一倍。

5.3.3 带深度限制的 Leaf-wise 的叶子生长策略

Level-wise 遍历一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。但实际上 Level-wise 是一种低效的算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销。实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。

Level-wise 是一层一层控制树的生长

Leaf-wise 则是一种更为高效的策略，每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。

• 因此同 Level-wise 相比，在分裂次数相同的情况下，Leaf-wise 可以降低更多的误差，得到更好的精度。
• Leaf-wise 的缺点是可能会长出比较深的决策树，产生过拟合。因此 LightGBM 在 Leaf-wise 之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

Leaf-wise 并不是一层一层的考虑，而是只考虑叶子节点（如果这个叶子节点需要划分则继续划分，如果不需要则不进行划分）

5.3.4 直接支持类别特征

实际上大多数机器学习工具都无法直接支持类别特征，一般需要把类别特征转化到多维的 0/1 特征，从而降低空间和时间的效率。

而类别特征的使用是在实践中很常用的。基于这个考虑，LightGBM 优化了对类别特征的支持，可以直接输入类别特征，不需要额外的 0/1 展开。并且 LightGBM 在决策树算法上增加了类别特征的决策规则。

在 EXPO 数据集上的实验，相比 0/1 展开的方法，直接使用类别特征则训练速度可以加速 8 倍，并且精度一致。目前来看，LightGBM 是第一个直接支持类别特征的 GBDT 工具。

EXPO 数据集介绍：EXPO Markers 数据集是一个用于实例分割和目标检测的 Expo 白板标记器数据集。该数据集包含三个子集（均包括实例分割标签）：Expo_Synt_V8 是一个包含 5000 张图像（1024x1024）的真实感合成图像数据集；Expo_Real_DGOffice 是一个包含 250 张图像（用于验证和测试）的真实图像数据集；Expo_Real_India 是一个包含 1000 张图像（用于训练和与我们的合成数据进行比较）的真实图像数据集。
数据集下载地址：expo_markers

5.3.5 直接支持高效并行

LightGBM 还具有支持高效并行的优点。LightGBM 原生支持并行学习，目前支持特征并行和数据并行的两种。

• 特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点，然后在机器间同步最优的分割点。
• 数据并行则是让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。

LightGBM 针对这两种并行方法都做了优化：

• 在特征并行算法中，通过在本地保存全部数据避免对数据切分结果的通信。

• 在数据并行中使用分散规约（Reduce scatter）把直方图合并的任务分摊到不同的机器，降低通信和计算，并利用直方图做差，进一步减少了一半的通信量。

• 基于投票的数据并行（Voting Parallelization）则进一步优化数据并行中的通信代价，使通信代价变成常数级别。在数据量很大的时候，使用投票并行可以得到非常好的加速效果。

6. LightGBM 算法 API 介绍

6.1 LightGBM的安装

pip install lightgbm

6.2 LightGBM 参数介绍

6.2.1 Control Parameters（控制参数）

Control Parameters 用于控制 LightGBM 的运行方式。

Control Parameters	含义	用法
max_depth	树的最大深度	当模型过拟合时，可以考虑首先降低 max_depth
min_data_in_leaf	叶子可能具有的最小记录数	默认 20，过拟合时用
feature_fraction	在每次迭代中随机选择多少的参数来建树（例如为 0.8 时，使用 80% 的参数）	Boosting 为 random forest 时用
bagging_fraction	每次迭代时用的数据比例	用于加快训练速度和减小过拟合
early_stopping_round	如果一次验证数据的一个度量在最近的 early_stopping_round 回合中没有提高，模型将停止训练	加速分析，减少过多的无效迭代
lambda	指定正则化	0 ~ 1
min_gain_to_split	描述分裂的最小 gain	控制树的有用的分裂
max_cat_group	在 group 边界上找到分割点	当类别数量很多时，找分割点很容易过拟合时
n_estimators	最大迭代次数	最大迭代数不必设置过大，可以在进行一次迭代后，根据最佳迭代数设置

一般 n_estimators 和 early_stopping_round 结合使用。

6.2.2 Core Parameters（核心参数）

Core Parameters 用于控制 LightGBM 模型的核心行为。

Core Parameters	含义	用法
Task	数据的用途	选择 train（训练）或者 predict（预测）
application	模型的用途	regression：回归 binary：二分类 multiclass：多分类
boosting	要用的算法	gbdt：Gradient Boosting Decision Tree，梯度提升决策树 rf：Random Forest，随机森林 dart：Dropouts meet Multiple Additive Regression Trees，Dropouts 遇见多元加法回归树 goss：Gradient-based One-Side Sampling，基于梯度的单侧采样
num_boost_round	迭代次数	通常 100+
learning_rate	学习率	常用 0.1/0.001/0.003/…
num_leaves	叶子数量	默认 31
device		cpu 或者 gpu
metric		mae：Mean Absolute Error，平均绝对误差 mse：Mean Squared Error，均方误差 binary_logloss：Binary Logarithmic Loss，二元对数损失 multi_logloss：Multiclass Logarithmic Loss，多类对数损失

其中：

• mae 用于衡量预测值与真实值之间的差异。

• mse 也用于衡量预测值与真实值之间的差异。

• binary_logloss 用于二元分类问题，用于衡量预测概率与真实标签之间的差异。

• multi_logloss 用于多类分类问题，用于衡量预测概率与真实标签之间的差异。

6.2.3 IO Parameters（输入输出参数）

IO Parameters 用于控制 LightGBM 的输入输出行为。

IO Parameters	含义
max_bin	表示 feature 将存入的 bin 的最大数量
categorical_feature	如果 categorical_features = 0, 1, 2，则列 0, 1, 2 是 categorical 变量
ignore_column	与 categorical_features 类似，只不过不是将特定的列视为 categorical，而是完全忽略
save_binary	这个参数为 True 时，则数据集被保存为二进制文件，下次读数据时速度会变快

6.3 调参建议

IO Parameters	含义
num_leaves	取值应 $<=2^{max\_depth}$，超过此值会导致过拟合
min_data_in_leaf	将它设置为较大的值可以避免生长太深的树，但可能会导致欠拟合。在大型数据集时就设置为数百或数千
max_depth	这个也是可以限制树的深度

下表对应了 Faster Speed（速度更快），Better Accuracy（精度更高），Over-fitting（防止过拟合）三种目的时，可以调的参数。

Faster Speed（速度更快）	Better Accuracy（精度更高）	Over-fitting（防止过拟合）
将 max_bin 设置小一些	用较大的 max_bin	max_bin 小一些
	num_leaves 大一些	num_leaves 小一些
用 feature_fraction 来做 sub-sampling		用 feature_fraction
用 bagging_fraction 和 bagging_freq		设定 bagging_fraction 和 bagging_freq
	training data多一些	training data 多一些
用 save_binary 来加速	直接用 categorical feature	用 gmin_data_in_leaf 和 n_sum_hessian_in_leaf
用 save_binary 来加速数据加载	直接用 categorical feature	用 gmin_data_in_leaf 和 min_sum_hessian_in_leaf
用 parallel learning	用 dart	用 lambda_l1, lambda_l2, min_gain_to_split 做正则化
	num_iterations 大一些，learning_rate 小一些	用 max_depth 控制树的深度

---

Q：Bagging 和 Boosting 有什么区别？
A：Bagging 和 Boosting 都是集成学习方法，它们通过组合多个模型来提高预测性能。

• Bagging（Bootstrap Aggregating）是一种并行集成方法，它通过从原始数据集中有放回地抽取多个子样本来训练多个模型。最终的预测结果是所有模型预测结果的平均值（回归问题）或投票结果（分类问题）。Bagging可以减少模型的方差，提高模型的稳定性。

• Boosting 是一种串行集成方法，它通过迭代地训练多个模型来提高预测性能。在每次迭代中，Boosting 都会根据上一次迭代的预测结果来调整样本权重，使得误分类的样本在下一次迭代中得到更多关注。最终的预测结果是所有模型预测结果的加权平均值。Boosting 可以减少模型的偏差和方差，提高模型的准确性。

总之，Bagging和Boosting的主要区别在于两者训练模型的方式不同：Bagging 是并行训练多个独立的模型，而 Boosting 是串行训练多个相互依赖的模型。

7. LightGBM 案例介绍

学习目标：

• 通过鸢尾花数据集知道 LightGBM 算法对应 API 的使用

接下来，通过鸢尾花数据集对 LightGBM 的基本使用，做一个介绍。

7.1 模型训练和模型评估

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
from lightgbm import early_stopping
from lightgbm import log_evaluation


# 1. 加载数据集
iris = load_iris()

data = iris.data
target = iris.target

# 2. 分割数据
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=22)

# 3. 模型训练
gbm = lgb.LGBMRegressor(objective="regression", learning_rate=0.05, n_estimators=20, device="gpu")  # n_estimators为迭代次数

gbm.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5)])

# 4. 模型评估
acc = gbm.score(x_test, y_test)
print(f"LightGBM 模型准确率为：{acc*100:.4f}%")

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[20]	valid_0's l1: 0.309316	valid_0's l2: 0.149031
LightGBM 模型准确率为：74.9762%

我们的代码成功地训练了一个 LightGBM 回归模型，并在测试集上获得了 74.9762% 的准确率。

在训练过程中，虽然我们使用了早停功能，但是模型并没有在 5 轮内满足早停条件，因此训练一直持续到了最大迭代次数（20次）。最终，模型在第 20 次迭代时获得了最佳验证结果，平均绝对误差（l1）为 0.309316，均方误差（l2）为 0.149031。

7.2 模型参数调优

# 定义需要优化的参数
param_grid_lst = {"learning_rate": [0.01, 0.1, 1],
                  "n_estimators": [20, 40, 70, 100]}

# 定义模型并使用网格搜索对模型进行包装
estimator = lgb.LGBMRegressor(num_leaves=31, device="GPU")
gbm = GridSearchCV(estimator=estimator, param_grid=param_grid_lst, cv=4)

# 模型训练
gbm.fit(x_train, y_train)

# 输出模型最优参数
print(f"通过网格搜索，LightGBM回归模型的最优参数为：\r\n{gbm.best_params_}")

通过网格搜索，LightGBM回归模型的最优参数为：
{'learning_rate': 0.1, 'n_estimators': 70}

7.3 基于最优参数再进行模型训练

# 基于最优参数再进行模型训练
gbm = lgb.LGBMRegressor(num_leaves=31, learning_rate=0.1, n_estimators=70)
gbm.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5), log_evaluation(period=1)])

acc = gbm.score(x_test, y_test)
print(f"基于最优参数的 LightGBM 模型准确率为：{acc*100:.4f}%")

[1]	valid_0's l1: 0.643338	valid_0's l2: 0.590069
Training until validation scores don't improve for 5 rounds
[2]	valid_0's l1: 0.586341	valid_0's l2: 0.495043
[3]	valid_0's l1: 0.535045	valid_0's l2: 0.417548
[4]	valid_0's l1: 0.488812	valid_0's l2: 0.354221
[5]	valid_0's l1: 0.445899	valid_0's l2: 0.298177
[6]	valid_0's l1: 0.409508	valid_0's l2: 0.253823
[7]	valid_0's l1: 0.379695	valid_0's l2: 0.219466
[8]	valid_0's l1: 0.352418	valid_0's l2: 0.189175
[9]	valid_0's l1: 0.328102	valid_0's l2: 0.165867
[10]	valid_0's l1: 0.304848	valid_0's l2: 0.145562
[11]	valid_0's l1: 0.283552	valid_0's l2: 0.128728
[12]	valid_0's l1: 0.263771	valid_0's l2: 0.112172
[13]	valid_0's l1: 0.246763	valid_0's l2: 0.100393
[14]	valid_0's l1: 0.233653	valid_0's l2: 0.0907631
[15]	valid_0's l1: 0.219299	valid_0's l2: 0.0823314
[16]	valid_0's l1: 0.206108	valid_0's l2: 0.0738624
[17]	valid_0's l1: 0.197188	valid_0's l2: 0.0686648
[18]	valid_0's l1: 0.186395	valid_0's l2: 0.0625122
[19]	valid_0's l1: 0.176682	valid_0's l2: 0.0573201
[20]	valid_0's l1: 0.167911	valid_0's l2: 0.0537077
[21]	valid_0's l1: 0.160387	valid_0's l2: 0.0510216
[22]	valid_0's l1: 0.154909	valid_0's l2: 0.0484569
[23]	valid_0's l1: 0.148458	valid_0's l2: 0.0462551
[24]	valid_0's l1: 0.143919	valid_0's l2: 0.044463
[25]	valid_0's l1: 0.139615	valid_0's l2: 0.043089
[26]	valid_0's l1: 0.136717	valid_0's l2: 0.0417173
[27]	valid_0's l1: 0.133302	valid_0's l2: 0.0406236
[28]	valid_0's l1: 0.12928	valid_0's l2: 0.0395706
[29]	valid_0's l1: 0.126451	valid_0's l2: 0.0388082
[30]	valid_0's l1: 0.122986	valid_0's l2: 0.0382606
[31]	valid_0's l1: 0.121381	valid_0's l2: 0.0375708
[32]	valid_0's l1: 0.119192	valid_0's l2: 0.0370738
[33]	valid_0's l1: 0.116589	valid_0's l2: 0.0367427
[34]	valid_0's l1: 0.115463	valid_0's l2: 0.0365167
[35]	valid_0's l1: 0.114311	valid_0's l2: 0.0360298
[36]	valid_0's l1: 0.112573	valid_0's l2: 0.0360516
[37]	valid_0's l1: 0.11149	valid_0's l2: 0.0361243
[38]	valid_0's l1: 0.110445	valid_0's l2: 0.0358674
[39]	valid_0's l1: 0.110027	valid_0's l2: 0.0355725
[40]	valid_0's l1: 0.109726	valid_0's l2: 0.0354881
[41]	valid_0's l1: 0.108879	valid_0's l2: 0.0356112
[42]	valid_0's l1: 0.108509	valid_0's l2: 0.0355532
[43]	valid_0's l1: 0.10854	valid_0's l2: 0.0353475
[44]	valid_0's l1: 0.107953	valid_0's l2: 0.0354961
[45]	valid_0's l1: 0.108035	valid_0's l2: 0.0354479
[46]	valid_0's l1: 0.108101	valid_0's l2: 0.0355342
[47]	valid_0's l1: 0.107894	valid_0's l2: 0.0356977
[48]	valid_0's l1: 0.107547	valid_0's l2: 0.0355966

Early stopping, best iteration is:
[43]	valid_0's l1: 0.10854	valid_0's l2: 0.0353475
基于最优参数的 LightGBM 模型准确率为：94.0648%

我们的代码成功地训练了一个基于最优参数的 LightGBM 回归模型，并在测试集上获得了 94.0648% 的准确率。

在代码中，我们使用了早停功能，并设置了early_stopping_rounds=5。这意味着，如果在连续 5 轮迭代中，验证集上的损失都没有改善，那么训练将提前结束。从输出结果来看，在第 43 次迭代时，模型在验证集上获得了最佳验证结果，平均绝对误差（l1）为 0.10854，均方误差（l2）为 0.0353475。在接下来的5轮迭代中（第 44 ~ 48 次迭代），验证集上的损失都没有改善。因此，在第 48 次迭代后，模型满足了早停条件，训练提前结束。

相比之前的模型，这个基于最优参数的模型在测试集上获得了更高的准确率（94.0648% > 74.9762%）。

8.《PUBG》玩家排名预测

8.1 项目背景

绝地求生（PlayerUnknown’s Battlegrounds，简称 PUBG）是一款大逃杀游戏，由 KRAFTON 公司开发。在游戏中，100 名玩家被投放到一个岛屿上，需要收集武器和装备，然后在不断缩小的安全区域内与其他玩家竞争，最后一个存活的玩家或队伍获胜。

PUBG 提供了多种不同的地图和游戏模式，包括单人、双人和四人小队模式。玩家可以通过合作、策略和技巧来获得胜利。

PUBG 可以在 PC、Xbox、PlayStation 和移动设备上免费游玩。

8.2 数据集介绍

本项目提供大量匿名的《PUBG》游戏统计数据。其格式为每行包含一个玩家的游戏后统计数据，列为数据的特征值。

数据来自所有类型的比赛：单排，双排，四排；不保证每场比赛有 100 名玩家，每组最多 4 名玩家。

• 数据集下载地址：PUBG Finish Placement Prediction (Kernels Only)

• 文件说明：

  • train_V2.csv：训练集
  • test_V2.csv：测试集

• 数据集中特征名称解释：

  • Id：用户 id
  • groupId：所处小队 id
  • matchId：该场比赛 id
  • assists：助攻数
  • boosts：使用能量、道具数量
  • DBNOs：击倒敌人数量
  • headshotKills：爆头数
  • heals：使用治疗药品数量
  • killPlace：本场比赛杀敌排行
  • killPoints：Elo 杀敌排名
  • kills：杀敌数
  • killStreaks：连续杀敌数
  • longestKill：最远杀敌距离
  • matchDuration：比赛时长
  • matchType：比赛类型（小组人数）
  • maxPlace：本场最差名次
  • numGroups：小组数量
  • rankPoints：Elo 排名
  • revives：救活队友的次数
  • rideDistance：驾车距离
  • roadKills：驾车杀敌数
  • swimDistance：游泳距离
  • teamKills：杀死队友的次数
  • vehicleDestorys：毁坏载具的数量
  • walkDistance：步行距离
  • weaponsAcquired：手机武器的数量
  • winPoints：Elo 胜率排名
  • winPlacePerc：百分比排名 —— 这是一个百分位获胜排名，其中1对应第一名，0对应比赛中最后一名

8.3 项目评估方式

我们必须创建一个模型，根据它们的最终统计数据预测玩家的排名，从 1（第一名）到 0（最后一名）。

最后结果通过平均绝对误差（MAE）进行评估，即通过预测的 winPlacePerc 和真实的 winPlacePerc 之间的平均绝对误差。

---

MAE（Mean Absolute Error，平均绝对误差）是一种用于衡量回归模型预测性能的指标。它计算了预测值与真实值之间的绝对误差的平均值。

from sklearn.metrics import mean_absolute_error

MAE 的计算公式为：

$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$

其中，$n$ 表示样本数量，$y_i$ 表示第 $i$ 个样本的真实值，${\hat{y}}_i$ 表示第 $i$ 个样本的预测值。

MAE 越小，说明模型的预测性能越好。当 MAE 为 0 时，说明模型在所有样本上的预测都完全准确。

8.4 代码实现

在接下来的分析中，我们将分析数据集并进行检测异常值。然后我们通过随机森林模型对其训练，并对该模型进行优化。

import pandas as pd
import matplotlib.pyplot as plt
from pylab import mpl
# 设置中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False
import numpy as np
import seaborn as sns

8.4.1 获取数据、基本数据信息查看

# 导入数据并且查看数据的基本情况
train = pd.read_csv("./data/pubg-finish-placement-prediction/train_V2.csv")

train.head()

train.tail()

train.describe()

train.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 4446966 entries, 0 to 4446965
Data columns (total 29 columns):
 #   Column           Dtype  
---  ------           -----  
 0   Id               object 
 1   groupId          object 
 2   matchId          object 
 3   assists          int64  
 4   boosts           int64  
 5   damageDealt      float64
 6   DBNOs            int64  
 7   headshotKills    int64  
 8   heals            int64  
 9   killPlace        int64  
 10  killPoints       int64  
 11  kills            int64  
 12  killStreaks      int64  
 13  longestKill      float64
 14  matchDuration    int64  
 15  matchType        object 
 16  maxPlace         int64  
 17  numGroups        int64  
 18  rankPoints       int64  
 19  revives          int64  
 20  rideDistance     float64
 21  roadKills        int64  
 22  swimDistance     float64
 23  teamKills        int64  
 24  vehicleDestroys  int64  
 25  walkDistance     float64
 26  weaponsAcquired  int64  
 27  winPoints        int64  
 28  winPlacePerc     float64
dtypes: float64(6), int64(19), object(4)
memory usage: 983.9+ MB

train.shape

(4446966, 29)

# 查看一共有多少场比赛
print(f"一共有 {np.unique(train['matchId']).shape} 场比赛")

# 查看一共有多少组（小队）
print(f"一共有 {np.unique(train['groupId']).shape} 组（小队）")

一共有 (47965,) 场比赛
一共有 (2026745,) 组（小队）

8.4.2 数据基本处理

8.4.2.1 数据缺失值处理

查看目标值，我们发现有一条样本，比较特殊，其“winPlacePerc”的值为 NaN，也就是目标值是缺失值。因为只有一个玩家是这样，我们直接将其对应行删除即可。

# 查看哪一行有缺失值
train[train.isnull().any(axis=1)]

# 删除缺失值所在行
train.dropna(inplace=True)

# 查看是否还有缺失值
np.any(train.isnull())

False

8.4.2.2 特征数据规范化处理

8.4.2.2.查看每场比赛参加的玩家数量

处理完缺失值之后，我们看一下每场游戏参加的人数会有多少，是每次都会匹配 100 个人才开始游戏吗？

# 显示每场比赛参数的玩家数量
# transform的作用类似实现了一个一对多的映射功能，把统计数量映射到对应的每个样本上
count = train.groupby("matchId")["matchId"].transform("count")

# 为DF对象添加一列
train["playersJoined"] = count

train["playersJoined"].head()

0    96
1    91
2    98
3    91
4    97
Name: playersJoined, dtype: int64

# 将每场参加的玩家人数升序排序
train["playersJoined"].sort_values().head()

1206365    2
2109739    2
3956552    5
3620228    5
696000     5
Name: playersJoined, dtype: int64

我们发现，不是每场必须满 100 人才开始游戏，最少的场次只有 2 个人。接下来我们对每场游戏的人数进行绘图。

# 绘制图像：查看每局开始的人数
# 通过seaborn下的countplot方法，可以直接绘制统计过数量之后的直方图
plt.figure(figsize=(20, 10), dpi=100)
sns.countplot(x=train["playersJoined"])
plt.title("游戏玩家数量")
plt.grid()
plt.show()

通过观察，发现一局游戏少于 75 个玩家的情况是很罕见的，大部分游戏都是在 96 人左右的时候才开始。

我们限制每局开始人数大于等于 75，再进行绘制。

猜想：把这些数据在后期加入数据处理，应该会得到的结果更加准确一些

# 再次绘制每局参加人数的直方图
plt.figure(dpi=200)
sns.countplot(x=train[train["playersJoined"] >= 75]["playersJoined"])
plt.title("游戏玩家数量")
plt.grid()
plt.show()

---

8.4.2.2.2 规范化输出部分数据

现在我们统计了“每局玩家数量”，那么我们就可以通过“每局玩家数量”来进一步考证其它特征，同时对其规范化设置试想：一局只有 70 个玩家的杀敌数，和一局有 100 个玩家的杀敌数，应该是不可以同时比较的。可以考虑的特征值包括：

1. kills（杀敌数）
2. damageDealt（总伤害）
3. maxPlace（本局最差名次）
4. matchDuration（比赛时长）

# 对部分特征值进行规范化处理
train["killsNorm"] = train["kills"] * ((100 - train["playersJoined"]) / 100 + 1)
train["damageDealtNorm"] = train["damageDealt"] * ((100 - train["damageDealt"]) / 100 + 1)
train["maxPlaceNorm"] = train["maxPlace"] * ((100 - train["maxPlace"]) / 100 + 1)
train["matchDurationNorm"] = train["matchDuration"] * ((100 - train["matchDuration"]) / 100 + 1)

# 比较经过规范化的特征值和原始特征值的值
to_show = ['Id', 'kills', 'killsNorm', 'damageDealt', 'damageDealtNorm', 
           'maxPlace', 'maxPlaceNorm', 'matchDuration', "matchDurationNorm"]

train[to_show][:]

Q：为什么使用 train[to_show][0:11]，而不是 train.loc[to_show][0:11]？
A：train[to_show][0:11] 和 train.loc[to_show][0:11] 是两种不同的索引方式。train[to_show] 是使用列标签来选择列，而 train.loc[to_show] 是使用行标签来选择行。

在这种情况下，我们希望选择特定的列，因此使用 train[to_show] 是正确的。然后，我们使用切片操作符 [0:11] 来选择前 11 行。

8.4.2.3 部分变量合成

此处我们把特征: heals（使用治疗药品数量）和 boosts（能量、道具使用数量）合并成一个新的变量，命名为“heas & boosts”，这是一个探索性过程，因为最后结果不一定有用😂。如果没有实际用处，最后再把它删除。

# 创建新变量 heals & boosts
train["heals & boosts"] = train["heals"] + train["boosts"]
train[["heals", "boosts", "heals & boosts"]].tail()

8.4.2.4 异常值处理

8.4.2.4.1 异常值处理：删除有击杀，但完全没有移动的玩家

异常数据处理：一些行中的数据统计出来的结果非常反常规，那么这些玩家肯定有问题。为了训练模型的准确性，我们会把这些异常数据剔除。

通过以下操作，识别出玩家在游戏中有击杀数，但是全局没有移动。这类型玩家肯定是存在异常情况（应该是开了），我们把这些玩家的数据删除掉，以免污染我们的数据集。

# 创建新变量，统计玩家移动距离
train["totalDistance"] = train["rideDistance"] + train["walkDistance"] + train["swimDistance"]

# 创建新变量，统计玩家是否在游戏中有击杀，但是没有移动：如果是则返回True，否则返回False
train["cheater"] = ((train["kills"] > 0) & (train["totalDistance"] == 0))  
# & 运算符用于对两个布尔 Series 对象进行逐元素逻辑与运算。

# 检查作弊人员的数量
train[train["cheater"] == True].shape[0]

1535

# 删除这些大哥的数据
train.drop(train[train["cheater"] == True].index, inplace=True)

# 检查作弊人员的数量
train[train["cheater"] == True].shape[0]

0

drop 是 Pandas DataFrame 对象的一个方法，用于删除指定的行或列。
上面代码首先使用布尔索引来选择 train 中所有被标记为作弊者的行。然后再使用 drop 方法来删除这些行，并使用 inplace=True 参数来指定在原地修改 DataFrame 对象。

8.4.2.4.2 异常值处理：删除驾车杀敌数异常的数据

# 删除载具杀敌超过10的玩家
train.drop(train[train["roadKills"] > 10].index, inplace=True)

8.4.2.4.3 异常值处理：删除一局中杀敌数超过30人的玩家数据

# 首先绘制玩家杀敌数的统计图
plt.figure(figsize=(10, 4), dpi=200)
sns.countplot(x=train["kills"])
plt.ylabel("达到的玩家人数")
plt.xlabel("击杀数")
plt.show()

# 再删除一局中杀敌数超过 30 人的玩家数据
train.drop(train[train["kills"] > 30].index, inplace=True)

8.4.2.4.4 异常值处理：删除爆头率异常数据

如果一个玩家的击杀爆头率过高且杀人数多，也说明其有问题。

# 创建爆头率变量
train["headshot_rate"] = train["headshotKills"] / train["kills"]

# 对于那些没有击杀记录的玩家，他们的爆头率将被设置为 0
train["headshot_rate"] = train["headshot_rate"].fillna(0)

# 绘制爆头率统计图
plt.figure(dpi=300)
sns.displot(train["headshot_rate"], bins=10, kde=False)
plt.ylabel("达到的玩家人数")
plt.xlabel("爆头率∈[0,1]")
plt.show()

# 删除爆头率异常的数据（爆头率 = 1 且击杀 > 9）
train.drop(train[(train["headshot_rate"] == 1) & (train["kills"] > 9)].index, inplace=True)

8.4.2.4.5 异常值处理：删除最远杀敌距离异常数据

# 绘制远距离杀敌直方图
plt.figure(dpi=300)
sns.displot(train["longestKill"], bins=10, kde=False)
plt.ylabel("达到的玩家人数")
plt.xlabel("远距离杀敌数")
plt.show()

# 删除杀敌距离 ≥ 1km 的玩家
train.drop(train[train["longestKill"] >= 1000].index, inplace=True)

8.4.2.4.6 异常值处理：删除关于运动距离的异常值

# 距离整体描述
train[["walkDistance", "rideDistance", "swimDistance", "totalDistance"]].describe()

# a. 删除行走距离异常的数据
train.drop(train[train["walkDistance"] >= 10000].index, inplace=True)

# b. 删除载具行驶距离异常的数据
train.drop(train[train["rideDistance"] >= 20000].index, inplace=True)

# c. 删除游泳距离异常的数据
train.drop(train[train["swimDistance"] >= 20000].index, inplace=True)

8.4.2.4.7 异常值处理：武器收集异常值处理

# 绘制武器收集直方图
plt.figure(dpi=300)
sns.displot(train["weaponsAcquired"], bins=10, kde=False)
plt.ylabel("达到的玩家人数")
plt.xlabel("武器收集数量")
plt.show()

# 删除武器收集异常的数据
train.drop(train[train["weaponsAcquired"] >= 80].index, inplace=True)

8.4.2.4.8 异常值处理：删除使用治疗药品数量异常值

# 绘制使用治疗药品数量直方图
plt.figure(figsize=(20, 10), dpi=300)
sns.displot(train["heals"], bins=10, kde=False)
plt.ylabel("达到的玩家人数")
plt.xlabel("使用治疗药品数量")
plt.savefig("./data/snsdisplot.png", dpi=300)
plt.show()

# 删除使用治疗药品数量异常的数据
train.drop(train[train["heals"] >= 40].index, inplace=True)

train.shape

(4444764, 38)

8.4.2.5 类别型数据处理

8.4.2.5.1 比赛类型 one-hot 处理

# 查看比赛类型
train["matchType"].unique()

array(['squad-fpp', 'duo', 'solo-fpp', 'squad', 'duo-fpp', 'solo',
       'normal-squad-fpp', 'crashfpp', 'flaretpp', 'normal-solo-fpp',
       'flarefpp', 'normal-duo-fpp', 'normal-duo', 'normal-squad',
       'crashtpp', 'normal-solo'], dtype=object)

# 对matchType进行one-hot编码
# 通过在后面添加的方式实现（并非替换）
train = pd.get_dummies(train, columns=["matchType"])

pd.get_dummies 是 Pandas 库中的一个函数，用于将分类变量转换为虚拟（或指示器）变量。

例如，假设有一个名为 df 的 DataFrame 对象，其中包含一个名为 color 的分类变量，它的值可能为 red、green 或 blue。可以使用 pd.get_dummies 函数来将这个分类变量转换为三个虚拟变量，如下所示：

dummies = pd.get_dummies(df['color'], prefix='color')

这将创建一个新的 DataFrame 对象，其中包含三列：color_red、color_green 和 color_blue。每一列都是一个虚拟变量，表示原始数据中 color 列的值是否等于相应的颜色。

train.shape

(4444764, 53)

# 通过正则匹配查看具体内容
matchType_encoding = train.filter(regex="matchType")  # 正则表达式 "matchType" 用于匹配包含字符串 "matchType" 的列名
matchType_encoding.head()

8.4.2.5.2 对 groupId，matchId 等数据进行处理

关于 groupId，matchId 这类型数据，也是类别型数据。但是它们的数据量特别多，如果我们使用 one-hot 编码，无异于自杀。在这里我们把它们变成用数字统计的类别型数据依旧不影响我们正常使用。

# 把 groupId 和 matchId 转换成类别类型 categorical types：就是把一堆不怎么好识别的内容转换成数字

# 转换 groupId
train["groupId"].head()

0    4d4b580de459be
1    684d5656442f9e
2    6a4a42c3245a74
3    a930a9c79cd721
4    de04010b3458dd
Name: groupId, dtype: object

# 使用 astype 方法将 groupId 列的数据类型转换为 category 类型
train["groupId"] = train["groupId"].astype("category")
train["groupId"].head()

0    4d4b580de459be
1    684d5656442f9e
2    6a4a42c3245a74
3    a930a9c79cd721
4    de04010b3458dd
Name: groupId, dtype: category
Categories (2026155, object): ['00000c08b5be36', '00000d1cbbc340', '000025a09dd1d7', '000038ec4dff53', ..., 'fffff305a0133d', 'fffff32bc7eab9', 'fffff7edfc4050', 'fffff98178ef52']

# 使用 .cat.codes 属性来获取每个类别的整数编码
train["groupId_category"] = train["groupId"].cat.codes
train["groupId_category"].head()

0     613593
1     827582
2     843273
3    1340072
4    1757336
Name: groupId_category, dtype: int32

# 转换 match_ID
train["matchId"] = train["matchId"].astype("category")
train["matchId_category"] = train["matchId"].cat.codes
train["matchId_category"].head()

0    30085
1    32751
2     3143
3    45260
4    20531
Name: matchId_category, dtype: int32

# 删除之前的列
train.drop(["groupId", "matchId"], axis=1, inplace=True)

# 查看新产生的列
train[["groupId_category", "matchId_category"]].head()

train.head()

8.4.2.6 数据截取

# 取前100万条数据进行训练
sample = 1000000
df_sample = train.sample(sample)
df_sample.head()

df_sample.shape

(1000000, 53)

8.4.2.7 确定特征值和目标值

# 确定特征值和目标值
df = df_sample.drop(["winPlacePerc", "Id"], axis=1)  # 删掉目标值和Id后就是特征值
y = df_sample["winPlacePerc"]  # 目标值

print(f"特征值形状为：{df.shape}")
print(f"目标值形状为：{y.shape}")

特征值形状为：(1000000, 51)
目标值形状为：(1000000,)

8.4.2.8 分割训练集和测试集

from sklearn.model_selection import train_test_split


x_train, x_test, y_train, y_test = train_test_split(df, y, test_size=0.2, random_state=22)

print(f"训练集样本形状为：{x_train.shape}")
print(f"训练集目标值形状为：{y_train.shape}")
print(f"测试集样本形状为：{x_test.shape}")
print(f"测试集目标值形状为：{y_test.shape}")

训练集样本形状为：(800000, 51)
训练集目标值形状为：(800000,)
测试集样本形状为：(200000, 51)
测试集目标值形状为：(200000,)

8.4.3 机器学习：模型训练和模型评估

# 导入训练和评估需要的库
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error

8.4.3.1 使用随机森林对模型进行训练

8.4.3.1.1 初步使用随机森林进行模型训练

# 定义模型（RandomForestRegressor类不支持使用GPU进行训练）
rfr = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features="sqrt", n_jobs=-1)

# 模型训练
rfr.fit(x_train, y_train)

y_pred = rfr.predict(x_test)
acc = rfr.score(x_test, y_test)
loss = mean_absolute_error(y_true=y_test, y_pred=y_pred)
print(f"RandomForestRegressor 模型准确率为：{acc*100:.4f}%")
print(f"RandomForestRegressor 模型损失为：{loss:.4f}")

RandomForestRegressor 模型准确率为：91.9824%
RandomForestRegressor 模型损失为：0.0618

8.4.3.1.2 再次使用随机森林，进行模型训练

这里我们减少特征值，以提高模型训练效率。

# 查看特征值在当前模型中的重要程度
rfr.feature_importances_

array([6.36844832e-03, 6.81794436e-02, 1.11574854e-02, 2.66158710e-03,
       6.40061510e-04, 3.39843901e-02, 1.78667987e-01, 2.04746962e-03,
       4.62923920e-03, 6.80113261e-03, 3.19364957e-02, 1.03808413e-02,
       6.28897020e-03, 7.50716288e-03, 3.56945114e-03, 1.06682174e-03,
       1.56785030e-02, 4.29282023e-05, 1.87206055e-03, 1.22616255e-04,
       7.35783213e-05, 1.97523185e-01, 7.65836266e-02, 2.35150792e-03,
       7.24096798e-03, 1.09228277e-02, 1.32039758e-02, 6.03694379e-03,
       1.03413350e-02, 7.02944988e-02, 1.97604305e-01, 0.00000000e+00,
       8.46825169e-04, 6.15972692e-05, 1.10975690e-06, 2.26440837e-04,
       5.28552743e-04, 4.54943040e-07, 2.06620463e-06, 0.00000000e+00,
       9.31087175e-05, 7.65156442e-07, 1.04664771e-05, 1.00306373e-06,
       3.03014790e-04, 2.24912063e-04, 1.05910252e-03, 1.28789662e-03,
       1.16530659e-03, 4.20894154e-03, 4.19858894e-03])

imp_df = pd.DataFrame({"cols": df.columns, "imp": rfr.feature_importances_})
imp_df.head()

imp_df = imp_df.sort_values(by="imp", ascending=False)  # 降序排序
imp_df.head()

# 要展示的特征数量
n_features = 20

# 创建一个颜色列表，其中每个颜色对应一个特征
colors = plt.cm.get_cmap('tab20')(range(n_features))

# 绘制条形图
plt.figure(figsize=(20, 8), dpi=200)
plt.barh(range(n_features), imp_df['imp'][:n_features], color=colors)
plt.yticks(range(n_features), imp_df['cols'][:n_features])
plt.xlabel("特征重要程度$\in [0, 1]$")
plt.ylabel("特征名称")
plt.show()

# 保留比较重要的特征
to_keep = imp_df[imp_df.imp > 0.005].cols
print(f"要保留的特征数量为：{len(to_keep)}")

to_keep

要保留的特征数量为：20
30        totalDistance
21         walkDistance
6             killPlace
22      weaponsAcquired
29       heals & boosts
1                boosts
5                 heals
10          longestKill
16         rideDistance
26      damageDealtNorm
2           damageDealt
25            killsNorm
11        matchDuration
28    matchDurationNorm
13            numGroups
24        playersJoined
9           killStreaks
0               assists
12             maxPlace
27         maxPlaceNorm
Name: cols, dtype: object

# 由这些比较重要的特征值生成新的DF对象
df_keep = df[to_keep]

# 重新划分数据集
x_train, x_test, y_train, y_test = train_test_split(df_keep, y, test_size=0.2, random_state=22)
print(f"[重新划分后] 训练集样本形状为：{x_train.shape}")
print(f"[重新划分后] 训练集目标值形状为：{y_train.shape}")
print(f"[重新划分后] 测试集样本形状为：{x_test.shape}")
print(f"[重新划分后] 测试集目标值形状为：{y_test.shape}")

[重新划分后] 训练集样本形状为：(800000, 20)
[重新划分后] 训练集目标值形状为：(800000,)
[重新划分后] 测试集样本形状为：(200000, 20)
[重新划分后] 测试集目标值形状为：(200000,)

# 再重新进行模型训练
rfr_keep = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features="sqrt", n_jobs=-1)
rfr_keep.fit(x_train, y_train)

# 再重新进行模型评估
y_pred = rfr_keep.predict(x_test)
acc = rfr_keep.score(x_test, y_test)
loss = mean_absolute_error(y_true=y_test, y_pred=y_pred)
print(f"[重新划分后] RandomForestRegressor 模型准确率为：{acc*100:.4f}%")
print(f"[重新划分后] RandomForestRegressor 模型损失为：{loss:.4f}")

[重新划分后] RandomForestRegressor 模型准确率为：92.3205%
[重新划分后] RandomForestRegressor 模型损失为：0.0601

8.4.3.2 使用 LightGBM 对模型进行训练

# 恢复到之前的数据分割状态
x_train, x_test, y_train, y_test = train_test_split(df, y, test_size=0.2, random_state=22)
print(f"训练集样本形状为：{x_train.shape}")
print(f"训练集目标值形状为：{y_train.shape}")
print(f"测试集样本形状为：{x_test.shape}")
print(f"测试集目标值形状为：{y_test.shape}")

训练集样本形状为：(800000, 51)
训练集目标值形状为：(800000,)
测试集样本形状为：(200000, 51)
测试集目标值形状为：(200000,)

8.4.3.2.1 模型初次尝试

import lightgbm as lgbm
from lightgbm import early_stopping
from lightgbm import log_evaluation


# 定义模型
lgbmr = lgbm.LGBMRegressor(objective="regression", num_leaves=31, 
                           learning_rate=0.05, n_estimatos=20, device="GPU")

# 模型训练
lgbmr.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5), log_evaluation(period=1)])

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[100]	valid_0's l1: 0.0607072	valid_0's l2: 0.00716562

# 模型预测
y_pred = lgbmr.predict(x_test, num_iteration=lgbmr.best_iteration_)
acc = lgbmr.score(x_test, y_test)
loss = mean_absolute_error(y_test, y_pred)
print(f"LGBMRegressor 模型准确率为：{acc*100:.4f}%")
print(f"LGBMRegressor 模型损失为：{loss:.4f}")

LGBMRegressor 模型准确率为：92.4044%
LGBMRegressor 模型损失为：0.0607

8.4.3.2.2 模型二次调优

from sklearn.model_selection import GridSearchCV

# 定义模型
model = lgbm.LGBMRegressor(num_leaves=31, device="gpu")
param_grid_lst = {"learning_rate": [0.01, 0.05, 0.1, 0.15, 0.2], 
                  "n_estimators": [20, 50, 100, 200, 300, 500]}

model = GridSearchCV(estimator=model, param_grid=param_grid_lst, cv=5, n_jobs=-1, verbose=2)
model.fit(x_train, y_train)

Fitting 5 folds for each of 30 candidates, totalling 150 fits

GridSearchCV(cv=5, estimator=LGBMRegressor(device='gpu'), n_jobs=-1,
             param_grid={'learning_rate': [0.01, 0.05, 0.1, 0.15, 0.2],
                         'n_estimators': [20, 50, 100, 200, 300, 500]},
             verbose=2)

此过程相当耗时

# 最优模型预测
y_pred = model.predict(x_test)
acc = model.score(x_test, y_test)
loss = mean_absolute_error(y_test, y_pred)
print(f"LGBMRegressor 网格交叉搜索最优模型准确率为：{acc*100:.4f}%")
print(f"LGBMRegressor 网格交叉搜索最优模型损失为：{loss:.4f}")

LGBMRegressor 网格交叉搜索最优模型准确率为：93.5980%
LGBMRegressor 网格交叉搜索最优模型损失为：0.0553

# 查看网格搜索/交叉验证的结果
print("Best parameters:", model.best_params_)
print("Best score:", model.best_score_)
print("Best estimator:", model.best_estimator_)
print("CV results:", model.cv_results_)

Best parameters: {'learning_rate': 0.15, 'n_estimators': 500}

Best score: 0.9359144823173906

Best estimator: LGBMRegressor(device='gpu', learning_rate=0.15, n_estimators=500)

CV results: {'mean_fit_time': array([14.34503574, 20.01631103, 25.97441425, 43.4136445 , 60.82093949,
       89.25930433, 11.62595191, 16.23543158, 25.54000373, 36.26000762,
       49.61888871, 66.26681533, 11.1753377 , 15.24283795, 20.54040017,
       30.36953435, 41.37112398, 52.48080788, 11.32525654, 16.418437  ,
       19.51573868, 29.89882855, 37.1528873 , 48.23137908, 10.68091936,
       13.80297165, 19.0142149 , 26.71594262, 33.4341989 , 34.97594118]), 'std_fit_time': array([0.89452845, 0.69153922, 1.30721953, 0.59971748, 1.47560355,
       1.69149272, 0.38846451, 0.26956315, 0.66550434, 0.40090513,
       0.64625266, 0.58125147, 0.81862829, 0.39151642, 0.25658152,
       1.89966286, 1.02374619, 2.16053993, 0.59936112, 1.262003  ,
       1.13085383, 1.16485342, 0.86350695, 0.98988553, 0.4670428 ,
       0.35239315, 0.6680641 , 0.72602143, 0.32089537, 3.72148617]), 'mean_score_time': array([1.5022016 , 1.42152162, 2.12359066, 4.06432238, 5.19431663,
       8.55703535, 1.32677093, 2.00913296, 2.52904983, 4.60726891,
       6.05252767, 9.39462171, 1.47626009, 1.72542372, 2.56810923,
       4.31121016, 6.6386538 , 9.39059463, 1.7088644 , 2.02408352,
       2.97478876, 4.52777481, 5.31689487, 7.65328541, 1.4070025 ,
       1.96806068, 2.37317958, 3.95138211, 4.22260122, 4.59180803]), 'std_score_time': array([0.26366997, 0.10020396, 0.14991592, 0.1966688 , 0.1009084 ,
       0.25914634, 0.12654092, 0.30676004, 0.37853699, 0.23382102,
       0.23462405, 0.40300067, 0.06112725, 0.07371341, 0.09753172,
       0.1741567 , 0.7262754 , 1.32623107, 0.21834994, 0.25155977,
       0.23926274, 0.52417874, 0.21302958, 0.12573272, 0.12746464,
       0.20380246, 0.0958619 , 0.18764002, 0.30194442, 0.14234936]), 'param_learning_rate': masked_array(data=[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05,
                   0.05, 0.05, 0.05, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.15,
                   0.15, 0.15, 0.15, 0.15, 0.15, 0.2, 0.2, 0.2, 0.2, 0.2,
                   0.2],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'param_n_estimators': masked_array(data=[20, 50, 100, 200, 300, 500, 20, 50, 100, 200, 300, 500,
                   20, 50, 100, 200, 300, 500, 20, 50, 100, 200, 300, 500,
                   20, 50, 100, 200, 300, 500],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'learning_rate': 0.01, 'n_estimators': 20}, {'learning_rate': 0.01, 'n_estimators': 50}, {'learning_rate': 0.01, 'n_estimators': 100}, {'learning_rate': 0.01, 'n_estimators': 200}, {'learning_rate': 0.01, 'n_estimators': 300}, {'learning_rate': 0.01, 'n_estimators': 500}, {'learning_rate': 0.05, 'n_estimators': 20}, {'learning_rate': 0.05, 'n_estimators': 50}, {'learning_rate': 0.05, 'n_estimators': 100}, {'learning_rate': 0.05, 'n_estimators': 200}, {'learning_rate': 0.05, 'n_estimators': 300}, {'learning_rate': 0.05, 'n_estimators': 500}, {'learning_rate': 0.1, 'n_estimators': 20}, {'learning_rate': 0.1, 'n_estimators': 50}, {'learning_rate': 0.1, 'n_estimators': 100}, {'learning_rate': 0.1, 'n_estimators': 200}, {'learning_rate': 0.1, 'n_estimators': 300}, {'learning_rate': 0.1, 'n_estimators': 500}, {'learning_rate': 0.15, 'n_estimators': 20}, {'learning_rate': 0.15, 'n_estimators': 50}, {'learning_rate': 0.15, 'n_estimators': 100}, {'learning_rate': 0.15, 'n_estimators': 200}, {'learning_rate': 0.15, 'n_estimators': 300}, {'learning_rate': 0.15, 'n_estimators': 500}, {'learning_rate': 0.2, 'n_estimators': 20}, {'learning_rate': 0.2, 'n_estimators': 50}, {'learning_rate': 0.2, 'n_estimators': 100}, {'learning_rate': 0.2, 'n_estimators': 200}, {'learning_rate': 0.2, 'n_estimators': 300}, {'learning_rate': 0.2, 'n_estimators': 500}], 'split0_test_score': array([0.28454907, 0.54923917, 0.76022635, 0.88293465, 0.91060857,
       0.9244634 , 0.76505124, 0.90190306, 0.92444864, 0.93187006,
       0.93394925, 0.93529471, 0.88553821, 0.92402019, 0.93150503,
       0.93446068, 0.9352919 , 0.93604723, 0.91159903, 0.92893752,
       0.93328694, 0.93504886, 0.93565664, 0.93623854, 0.91960025,
       0.93077007, 0.93357905, 0.93492508, 0.93552697, 0.93608738]), 'split1_test_score': array([0.28436306, 0.54875665, 0.75954484, 0.88222918, 0.91018844,
       0.92418283, 0.76438739, 0.90153518, 0.92425756, 0.9319695 ,
       0.934071  , 0.93554092, 0.8849283 , 0.92402688, 0.93171493,
       0.93470062, 0.93560521, 0.93640918, 0.91033221, 0.92893088,
       0.93318294, 0.93526183, 0.9358338 , 0.93635082, 0.91873591,
       0.93101601, 0.93364595, 0.93507168, 0.93551916, 0.93595913]), 'split2_test_score': array([0.2843355 , 0.54855371, 0.75959117, 0.88183133, 0.91004533,
       0.92409252, 0.764491  , 0.90155836, 0.92413334, 0.93163902,
       0.93377787, 0.93513166, 0.88560984, 0.92399051, 0.93142455,
       0.93422112, 0.93510549, 0.93571943, 0.91129593, 0.92855244,
       0.93301829, 0.93474559, 0.93526989, 0.93578894, 0.91839872,
       0.93037481, 0.93342368, 0.93463735, 0.93512018, 0.93561078]), 'split3_test_score': array([0.28416371, 0.54822298, 0.75871174, 0.88129364, 0.90952787,
       0.923619  , 0.76384192, 0.90058734, 0.92375681, 0.93143612,
       0.93350314, 0.93487847, 0.88453036, 0.92307768, 0.93082085,
       0.93394062, 0.9348608 , 0.93564594, 0.90959224, 0.92776206,
       0.9324688 , 0.93431994, 0.93499641, 0.93558379, 0.91865493,
       0.93035951, 0.93341205, 0.93466532, 0.93519394, 0.93567325]), 'split4_test_score': array([0.28496283, 0.54958736, 0.76029536, 0.8823003 , 0.91004134,
       0.92396112, 0.76498543, 0.90173034, 0.92393124, 0.93143822,
       0.93352341, 0.93492248, 0.88570397, 0.92331548, 0.9307633 ,
       0.93378324, 0.93464401, 0.93540764, 0.91073014, 0.92823403,
       0.93259306, 0.93435349, 0.93502704, 0.93561031, 0.91849981,
       0.93000466, 0.93288866, 0.93428614, 0.93477511, 0.93522242]), 'mean_test_score': array([0.28447483, 0.54887197, 0.75967389, 0.88211782, 0.91008231,
       0.92406378, 0.7645514 , 0.90146286, 0.92410552, 0.93167058,
       0.93376493, 0.93515365, 0.88526213, 0.92368615, 0.93124573,
       0.93422126, 0.93510148, 0.93584588, 0.91070991, 0.92848339,
       0.93291001, 0.93474594, 0.93535676, 0.93591448, 0.91877793,
       0.93050501, 0.93338988, 0.93471711, 0.93522707, 0.93571059]), 'std_test_score': array([0.00027289, 0.00048629, 0.00057283, 0.000543  , 0.00034602,
       0.00027679, 0.00044094, 0.00045743, 0.00024232, 0.00021868,
       0.00022569, 0.00024475, 0.00045591, 0.00040693, 0.00038279,
       0.00033398, 0.00033383, 0.0003481 , 0.0007108 , 0.00044581,
       0.00032355, 0.0003724 , 0.00033574, 0.00032033, 0.00042761,
       0.0003521 , 0.00026616, 0.00026972, 0.00028002, 0.00030113]), 'rank_test_score': array([30, 29, 28, 26, 23, 19, 27, 24, 18, 14, 11,  6, 25, 20, 15, 10,  7,
        2, 22, 17, 13,  8,  4,  1, 21, 16, 12,  9,  5,  3])}

8.4.3.2.3 模型三次调优

acc_lst = []
loss_lst = []
n_estimators_lst = [50, 100, 300, 500, 1000]

for n in n_estimators_lst:
    lgbmr = lgbm.LGBMRegressor(boosting_type="gbdt", num_leaves=31,
                               max_depth=5, learning_rate=0.1,n_estimators=n, 
                               min_child_samples=20, n_jobs=-1, device="gpu")
    lgbmr.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5)])
    y_pred = lgbmr.predict(x_test)
    acc = lgbmr.score(x_test, y_test)
    loss = mean_absolute_error(y_test, y_pred)
    acc_lst.append(acc)
    loss_lst.append(loss)
    print(f"[n_estimators = {n}] LGBMRegressor 模型准确率为：{acc*100:.4f}%")
    print(f"[n_estimators = {n}] LGBMRegressor 模型损失为：{loss:.4f}\r\n")

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[50]	valid_0's l1: 0.0622125	valid_0's l2: 0.00769457
[n_estimators = 50] LGBMRegressor 模型准确率为：91.8437%
[n_estimators = 50] LGBMRegressor 模型损失为：0.0622

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[100]	valid_0's l1: 0.0587449	valid_0's l2: 0.00682084
[n_estimators = 100] LGBMRegressor 模型准确率为：92.7698%
[n_estimators = 100] LGBMRegressor 模型损失为：0.0587

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[300]	valid_0's l1: 0.056226	valid_0's l2: 0.00621857
[n_estimators = 300] LGBMRegressor 模型准确率为：93.4083%
[n_estimators = 300] LGBMRegressor 模型损失为：0.0562

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[500]	valid_0's l1: 0.0556214	valid_0's l2: 0.00610183
[n_estimators = 500] LGBMRegressor 模型准确率为：93.5320%
[n_estimators = 500] LGBMRegressor 模型损失为：0.0556

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[542]	valid_0's l1: 0.0555619	valid_0's l2: 0.00609029
[n_estimators = 1000] LGBMRegressor 模型准确率为：93.5442%
[n_estimators = 1000] LGBMRegressor 模型损失为：0.0556

# 画图展示
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4), dpi=200)

acc_lst_percent = [i * 100 for i in acc_lst]
axes[0].scatter(n_estimators_lst, acc_lst_percent, color='red', zorder=10)
axes[0].plot(n_estimators_lst, acc_lst_percent)
axes[0].set_xlabel("n_estimators")
axes[0].set_ylabel("准确率")

axes[1].scatter(n_estimators_lst, loss_lst, color='red', zorder=10)
axes[1].plot(n_estimators_lst, loss_lst)
axes[1].set_xlabel("n_estimators")
axes[1].set_ylabel("Loss")
plt.show()

print(f"最优 n_estimators 为：{n_estimators_lst[np.argmin(loss_lst)]}")

最优 n_estimators 为：1000

---

接下来可以照猫画虎调整 max_depth 参数。

acc_lst = []
loss_lst = []
max_depth_lst = [1, 3, 5, 7, 9, 11]

for n in max_depth_lst:
    lgbmr = lgbm.LGBMRegressor(boosting_type="gbdt", num_leaves=31,
                               max_depth=n, learning_rate=0.1,n_estimators=1000, 
                               min_child_samples=20, n_jobs=-1, device="gpu")
    lgbmr.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5)])
    y_pred = lgbmr.predict(x_test)
    acc = lgbmr.score(x_test, y_test)
    loss = mean_absolute_error(y_test, y_pred)
    acc_lst.append(acc)
    loss_lst.append(loss)
    print(f"[max_depth = {n}] LGBMRegressor 模型准确率为：{acc*100:.4f}%")
    print(f"[max_depth = {n}] LGBMRegressor 模型损失为：{loss:.4f}\r\n")
    

# 绘图展示结果
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4), dpi=200)

acc_lst_percent = [i * 100 for i in acc_lst]
axes[0].scatter(max_depth_lst, acc_lst_percent, color='red', zorder=10)
axes[0].plot(max_depth_lst, acc_lst_percent)
axes[0].set_xlabel("max_depth")
axes[0].set_ylabel("准确率")

axes[1].scatter(max_depth_lst, loss_lst, color='red', zorder=10)
axes[1].plot(max_depth_lst, loss_lst)
axes[1].set_xlabel("max_depth")
axes[1].set_ylabel("Loss")
plt.show()

print(f"最优 max_depth 为：{max_depth_lst[np.argmin(loss_lst)]}")

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[999]	valid_0's l1: 0.077615	valid_0's l2: 0.0114374
[max_depth = 1] LGBMRegressor 模型准确率为：87.8763%
[max_depth = 1] LGBMRegressor 模型损失为：0.0776

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[1000]	valid_0's l1: 0.0569189	valid_0's l2: 0.0063635
[max_depth = 3] LGBMRegressor 模型准确率为：93.2546%
[max_depth = 3] LGBMRegressor 模型损失为：0.0569

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[542]	valid_0's l1: 0.0555619	valid_0's l2: 0.00609032
[max_depth = 5] LGBMRegressor 模型准确率为：93.5442%
[max_depth = 5] LGBMRegressor 模型损失为：0.0556

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[729]	valid_0's l1: 0.0550689	valid_0's l2: 0.00599715
[max_depth = 7] LGBMRegressor 模型准确率为：93.6430%
[max_depth = 7] LGBMRegressor 模型损失为：0.0551

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[597]	valid_0's l1: 0.0552526	valid_0's l2: 0.00602691
[max_depth = 9] LGBMRegressor 模型准确率为：93.6114%
[max_depth = 9] LGBMRegressor 模型损失为：0.0553

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[675]	valid_0's l1: 0.0551284	valid_0's l2: 0.00601711
[max_depth = 11] LGBMRegressor 模型准确率为：93.6218%
[max_depth = 11] LGBMRegressor 模型损失为：0.0551

最优 max_depth 为：7

---

接下来可以照猫画虎调整 learning_rate 参数。

acc_lst = []
loss_lst = []
learning_rate_lst = [0.01, 0.05, 0.1, 0.15, 0.2, 0.35, 0.5]

for n in learning_rate_lst:
    lgbmr = lgbm.LGBMRegressor(boosting_type="gbdt", num_leaves=31,
                               max_depth=7, learning_rate=n, n_estimators=1000, 
                               min_child_samples=20, n_jobs=-1, device="gpu")
    lgbmr.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5)])
    y_pred = lgbmr.predict(x_test)
    acc = lgbmr.score(x_test, y_test)
    loss = mean_absolute_error(y_test, y_pred)
    acc_lst.append(acc)
    loss_lst.append(loss)
    print(f"[learning_rate = {n}] LGBMRegressor 模型准确率为：{acc*100:.4f}%")
    print(f"[learning_rate = {n}] LGBMRegressor 模型损失为：{loss:.4f}\r\n")
    

# 绘图展示结果
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4), dpi=200)

acc_lst_percent = [i * 100 for i in acc_lst]
axes[0].scatter(learning_rate_lst, acc_lst_percent, color='red', zorder=10)
axes[0].plot(learning_rate_lst, acc_lst_percent)
axes[0].set_xlabel("learning_rate")
axes[0].set_ylabel("准确率")

axes[1].scatter(learning_rate_lst, loss_lst, color='red', zorder=10)
axes[1].plot(learning_rate_lst, loss_lst)
axes[1].set_xlabel("learning_rate")
axes[1].set_ylabel("Loss")
plt.show()

print(f"最优 learning_rate 为：{learning_rate_lst[np.argmin(loss_lst)]}")

Training until validation scores don't improve for 5 rounds
Did not meet early stopping. Best iteration is:
[1000]	valid_0's l1: 0.0577028	valid_0's l2: 0.00653157
[learning_rate = 0.01] LGBMRegressor 模型准确率为：93.0765%
[learning_rate = 0.01] LGBMRegressor 模型损失为：0.0577

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[855]	valid_0's l1: 0.0553832	valid_0's l2: 0.00604542
[learning_rate = 0.05] LGBMRegressor 模型准确率为：93.5918%
[learning_rate = 0.05] LGBMRegressor 模型损失为：0.0554

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[729]	valid_0's l1: 0.0550692	valid_0's l2: 0.00599728
[learning_rate = 0.1] LGBMRegressor 模型准确率为：93.6428%
[learning_rate = 0.1] LGBMRegressor 模型损失为：0.0551

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[415]	valid_0's l1: 0.0553472	valid_0's l2: 0.0060467
[learning_rate = 0.15] LGBMRegressor 模型准确率为：93.5904%
[learning_rate = 0.15] LGBMRegressor 模型损失为：0.0553

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[313]	valid_0's l1: 0.0556364	valid_0's l2: 0.00610478
[learning_rate = 0.2] LGBMRegressor 模型准确率为：93.5289%
[learning_rate = 0.2] LGBMRegressor 模型损失为：0.0556

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[215]	valid_0's l1: 0.05624	valid_0's l2: 0.0062342
[learning_rate = 0.35] LGBMRegressor 模型准确率为：93.3917%
[learning_rate = 0.35] LGBMRegressor 模型损失为：0.0562

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[158]	valid_0's l1: 0.0566002	valid_0's l2: 0.00632119
[learning_rate = 0.5] LGBMRegressor 模型准确率为：93.2995%
[learning_rate = 0.5] LGBMRegressor 模型损失为：0.0566

最优 learning_rate 为：0.1

---

最佳模型性能如下：

best_model = lgbm.LGBMRegressor(boosting_type="gbdt", num_leaves=31,
                           max_depth=7, learning_rate=0.10, n_estimators=1000, 
                           min_child_samples=20, n_jobs=-1, device="gpu")
best_model.fit(x_train, y_train, eval_set=[(x_test, y_test)], eval_metric="l1", callbacks=[early_stopping(5)])
y_pred = best_model.predict(x_test)
acc = best_model.score(x_test, y_test)
loss = mean_absolute_error(y_test, y_pred)
acc_lst.append(acc)
loss_lst.append(loss)
print(f"LGBMRegressor 最佳模型准确率为：{acc*100:.4f}%")
print(f"LGBMRegressor 最佳模型损失为：{loss:.4f}\r\n")

Training until validation scores don't improve for 5 rounds
Early stopping, best iteration is:
[729]	valid_0's l1: 0.0550691	valid_0's l2: 0.00599729
LGBMRegressor 最佳模型准确率为：93.6428%
LGBMRegressor 最佳模型损失为：0.0551

8.4.3.2.4 模型调优两种方式对比

在上面的代码中，我们在循环中对不同的参数进行了调优。在每次循环中，您都使用了一个不同的单一参数值来训练一个 LGBMRegressor 模型，并计算了模型的准确率和损失。

这种方法比使用 GridSearchCV 快，是因为我们只调整了一个参数，而且只尝试了 有限个 个不同的值。相比之下，GridSearchCV 会对多个参数进行调优，并且会尝试每个参数的所有可能值。因此，使用 GridSearchCV 需要更多的计算。

但是，我们需要注意的是，这种方法只能调整一个参数，而且只能尝试有限个值。如果我们想要同时调整多个参数，并且尝试更多的值，那么使用 GridSearchCV 或其他自动调参方法可能会更方便。

想调优多个参数还是要使用 GridSearchCV😄

8.4.3.3 不同算法模型效果对比

算法名称	准确率	MAE损失
RandomForestRegressor	91.9824%	0.0618
[重新划分数据集后] RandomForestRegressor	92.3205%	0.0601
LGBMRegressor	92.4044%	0.0607
[GridSearchCV] LGBMRegressor	93.5980%	0.0553
[手动调参] LGBMRegressor	93.6428%	0.0551

algorithm_names = ["RandomForestRegressor", "[重新划分数据集后] RandomForestRegressor", "LGBMRegressor", "[GridSearchCV] LGBMRegressor", "[手动调参] LGBMRegressor"]
x_label = [f"算法{i}" for i in range(1, len(algorithm_names) + 1)]
accs = [91.9824, 92.3205, 92.4044, 93.5980, 93.6428]
losses = [0.0618, 0.0601, 0.0607, 0.0553, 0.0551]

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 6), dpi=200)
for x, y, label in zip(x_label, accs, algorithm_names):
    axes[0].scatter(x, y, zorder=10, label=label)
axes[0].plot(x_label, accs)
axes[0].set_xlabel("learning_rate")
axes[0].set_ylabel("Accuracy")
axes[0].set_title("不同算法准确率对比")
axes[0].legend()

for x, y, label in zip(x_label, losses, algorithm_names):
    axes[1].scatter(x, y, zorder=10, label=label)
axes[1].plot(x_label, losses)
axes[1].set_xlabel("learning_rate")
axes[1].set_ylabel("Loss")
axes[1].set_title("不同算法损失对比")
axes[1].legend()
plt.show()