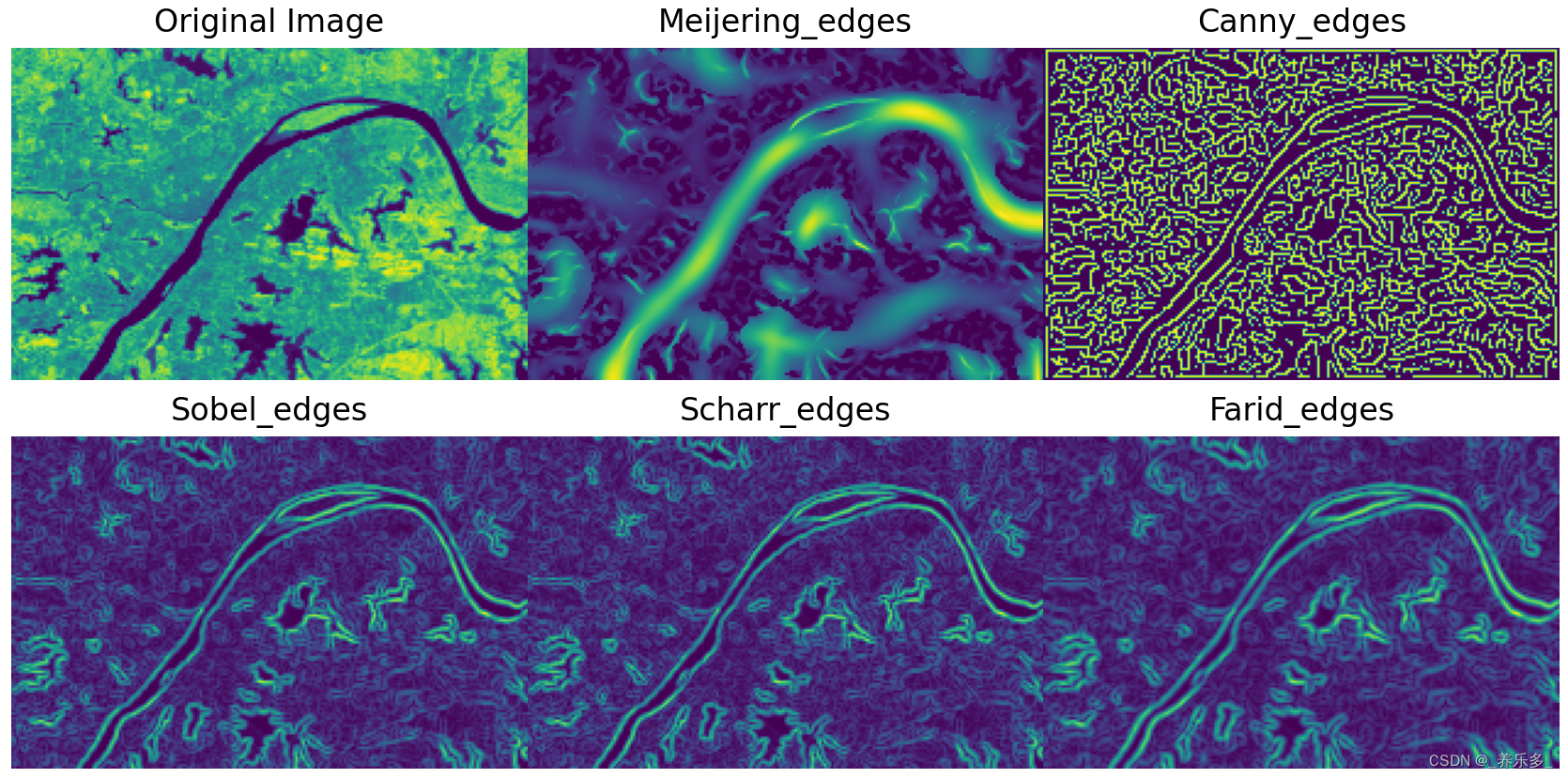
在上篇博客中,我简单比较了瑞丽伯纳德对流的FTLE场,但是因为粒子追踪采用的是欧拉方法,所以精度不是很高, 因此与文献中的结果还是有些差别。
下面放一张文献中的FTLE场,参数与上篇文章是一致的,Ra = 1e8;Pr = 1;
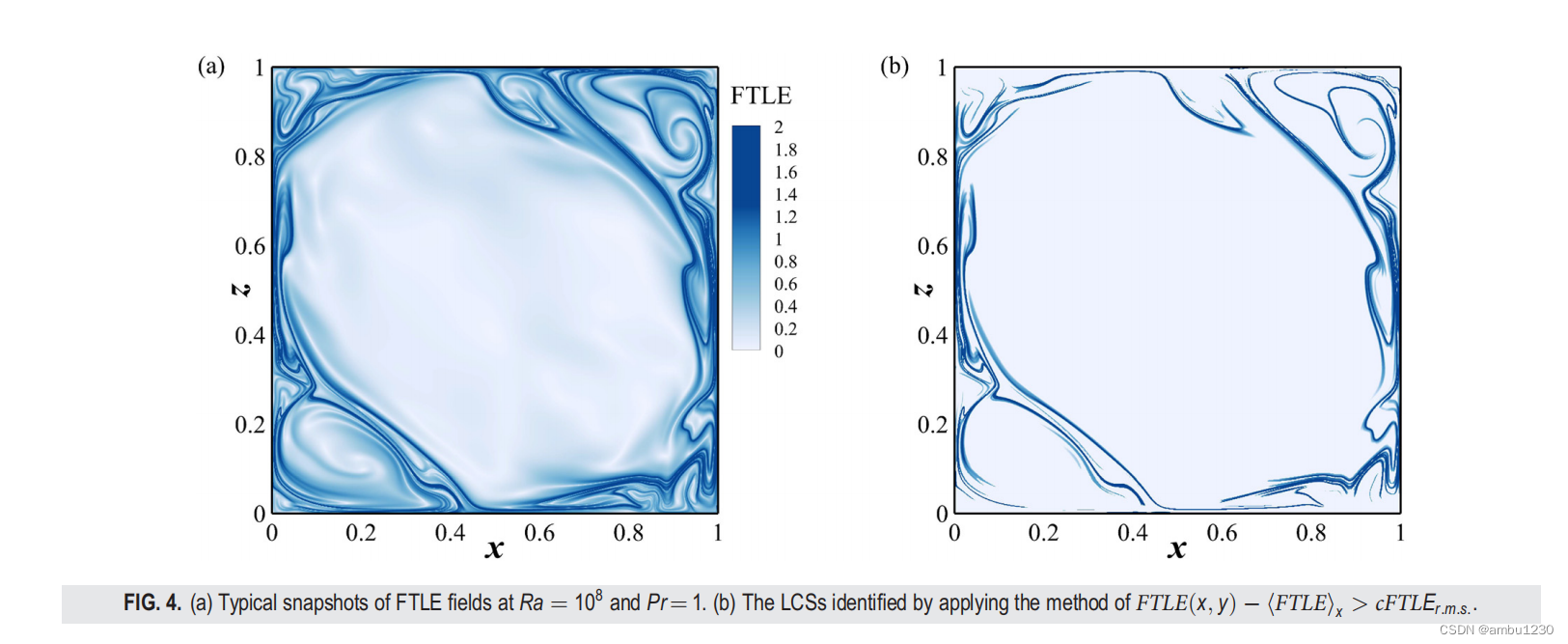
本文将详细的介绍如何得到这样的图片,好吧,其实也不是很详细。总之,先展示以下我个人的结果。
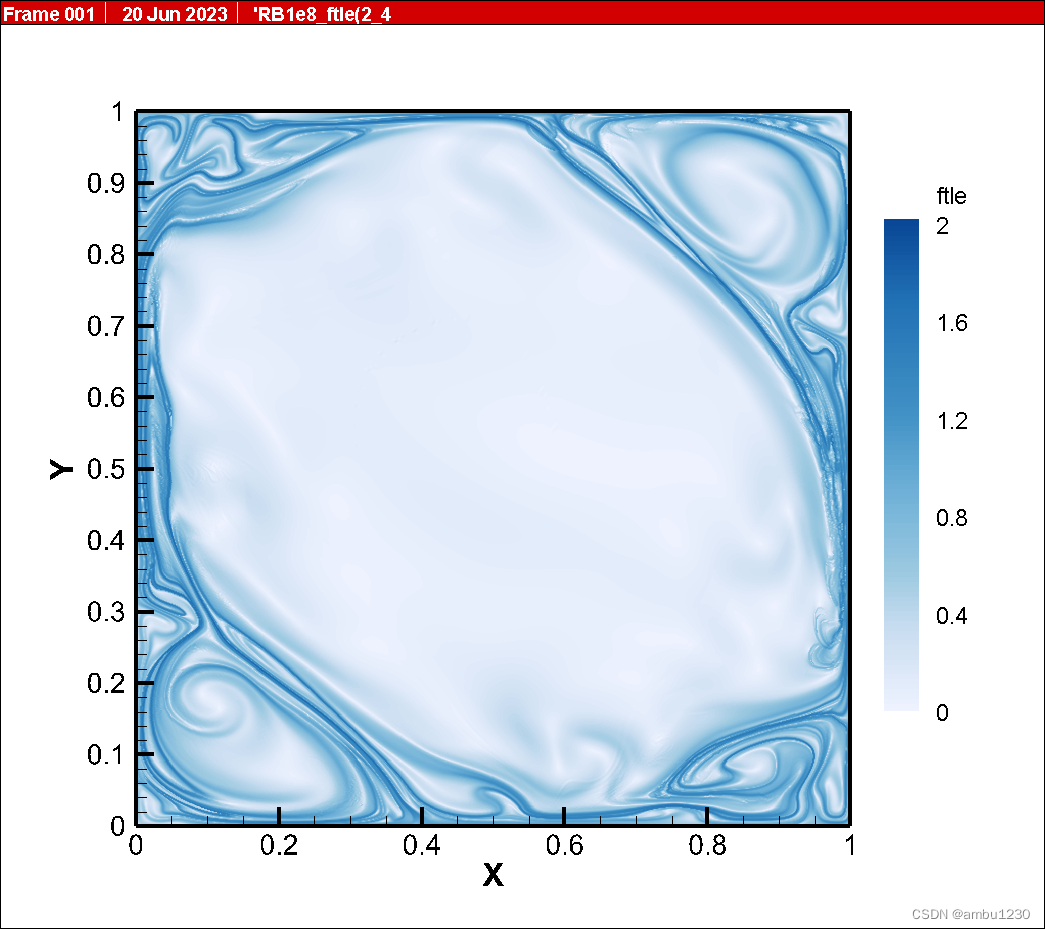
可以看出,上图基本上与文献是一致的,因为这里展示的是瞬时场,所以当然不可能是完全一致,至于提取的LCS结构,我在下面也会提及。
本着详细介绍的原则,所以这里我很良心的从流场计算开始介绍。粒子迁移需要时空离散的流场数据。流场的网格是很好确定的,我这里是DNS,所以网格尺度小于 η \eta η就行。比较重要的是时间步长应该取多少。
1、流场时间步长
首先,根据我的计算参数,我得到流场的无量纲时间
t
f
=
1.13
s
t_f=1.13s
tf=1.13s。根据文献,
t
E
=
7
t
f
=
7.9
s
t_E=7t_f=7.9s
tE=7tf=7.9s
即一个turn over time(大涡转一圈的时间)。因为积分时间选取为
1
/
2
t
E
1/2t_E
1/2tE,所以我这里就凑个整,总共计算8s,积分时间选择4s,然后又凑个整,时间步长分别选取为0.1和0.05,总共为80个和160个时间步,时间步肯定是越小越好,但是存储量也会迅速上升,这里后面会比较这两个时间步得到的结果。
上面我放的图是dt=0.05得到的结果,我们先来以这个为例。
2、积分时间
这个其实文献里已经比较清楚了,我这里还是啰嗦一句。讲一讲如何获得
turn ove time 大涡转一圈的时间,
t
E
=
4
π
/
<
w
c
>
t
t_E=4\pi/<w_c>_t
tE=4π/<wc>t
我们知道,涡量,也就是速度的旋度,它还等于角速度的两倍,不会的可以去翻书,再不会放弃流体力学吧。这里的思想就是,将转动的大涡看成是一个刚体,所以用中心处的角速度来作为大涡整体的角速度。所以根据这个我们可以得到
t
E
t_E
tE。
注意,这里的
w
c
w_c
wc,是有量纲的,即
T
−
1
T^{-1}
T−1,我们需要对其乘以一个
t
f
t_f
tf来对其进行无量纲化,这样才能得到无量纲的
t
f
t_f
tf。这一点文献中没提,但基本上大家都是默认这样操作。
我这里也对文献中的数据进行了验证,分别计算了努塞尔数和
t
E
t_E
tE。结果其实还行,因为本身统计时间太短了,没有考虑统计稳态,统计收敛这些问题。
结果放在这里,供大家参考。
计算0-8时刻内的努塞尔数
Nu:25.35 文献值:25.29
tE:7.202612960718049 文献值: 7.0;
2.1、积分时间的影响
文献中指出,积分时间大于tE时,FTLE场的差别其实不大,下面来看一下我的计算结果。
积分时间:3.6s,见下图
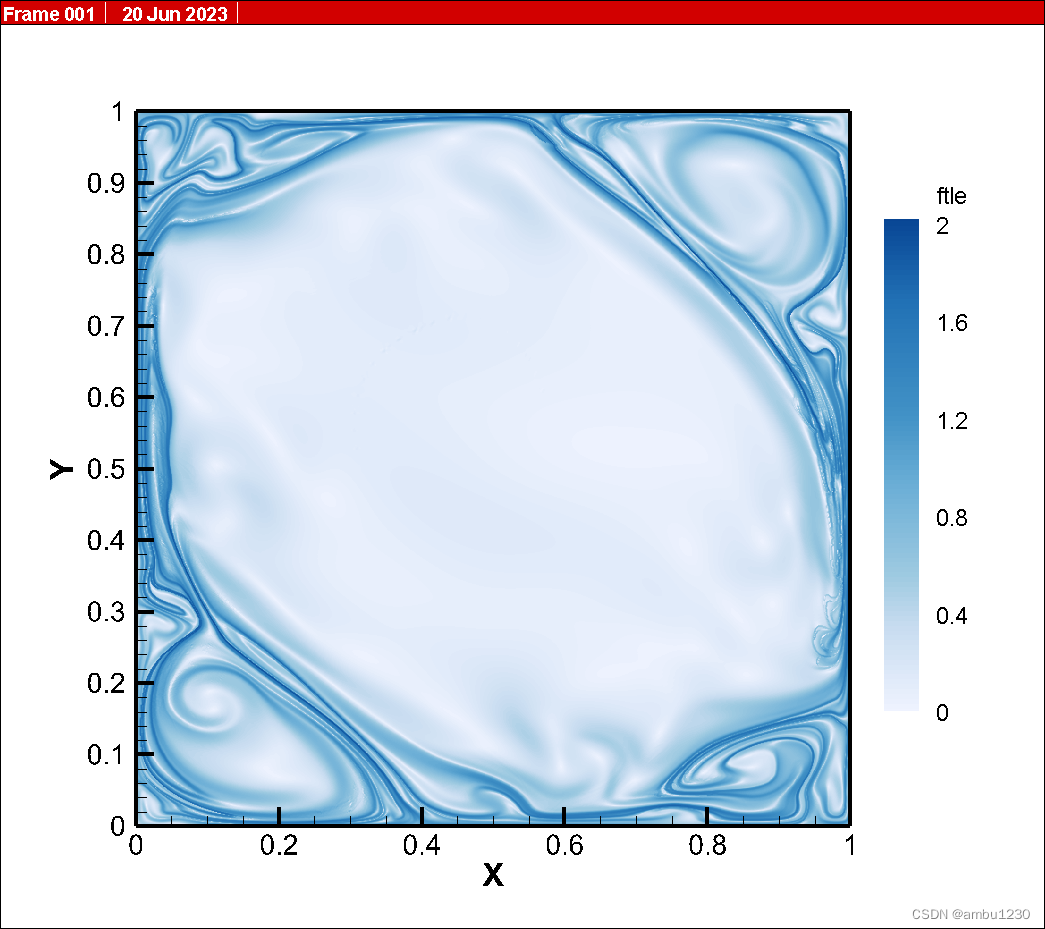
积分时间:4s:见第二张图。
积分时间:5s,见下图
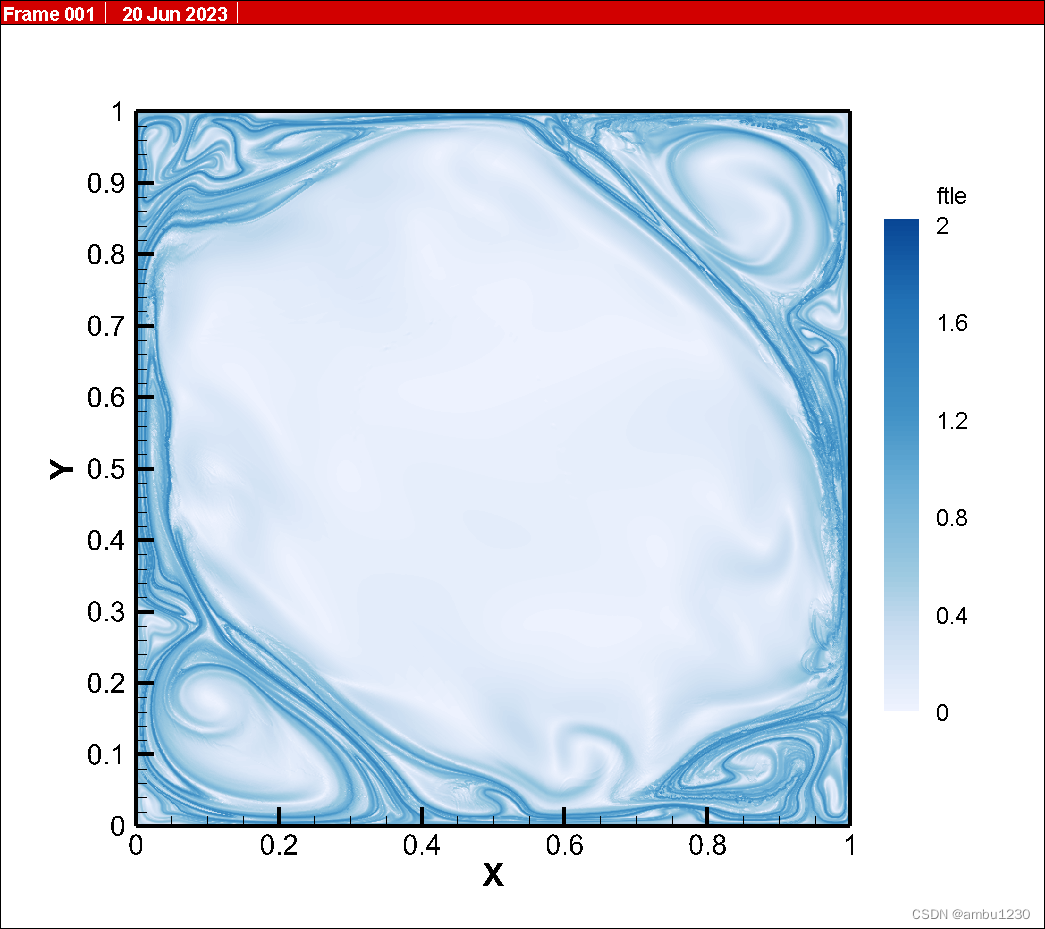
可以看出基本的形状是没有发生什么变化的,只不过因为积分时间过长,FTLE的值会变小,这是由于计算FTLE时需要除以时间。
但是基本的结论与文献是保持一致的,这里通过比较发现其实t=3.6s和4s时的结果是比较好的,积分时间为5s能看到有些地方不是那么清晰,可能是由于粒子推进误差的问题。
3、粒子个数的问题
在计算FTLE场时,初始放置的粒子不一定要与网格数保持一致,是可以自由确定的。
我们固定积分时间为4s,即0.5tE,看一下粒子数对FTLE场计算的影响。
粒子数512*512,与流场网格保持一致,如下图
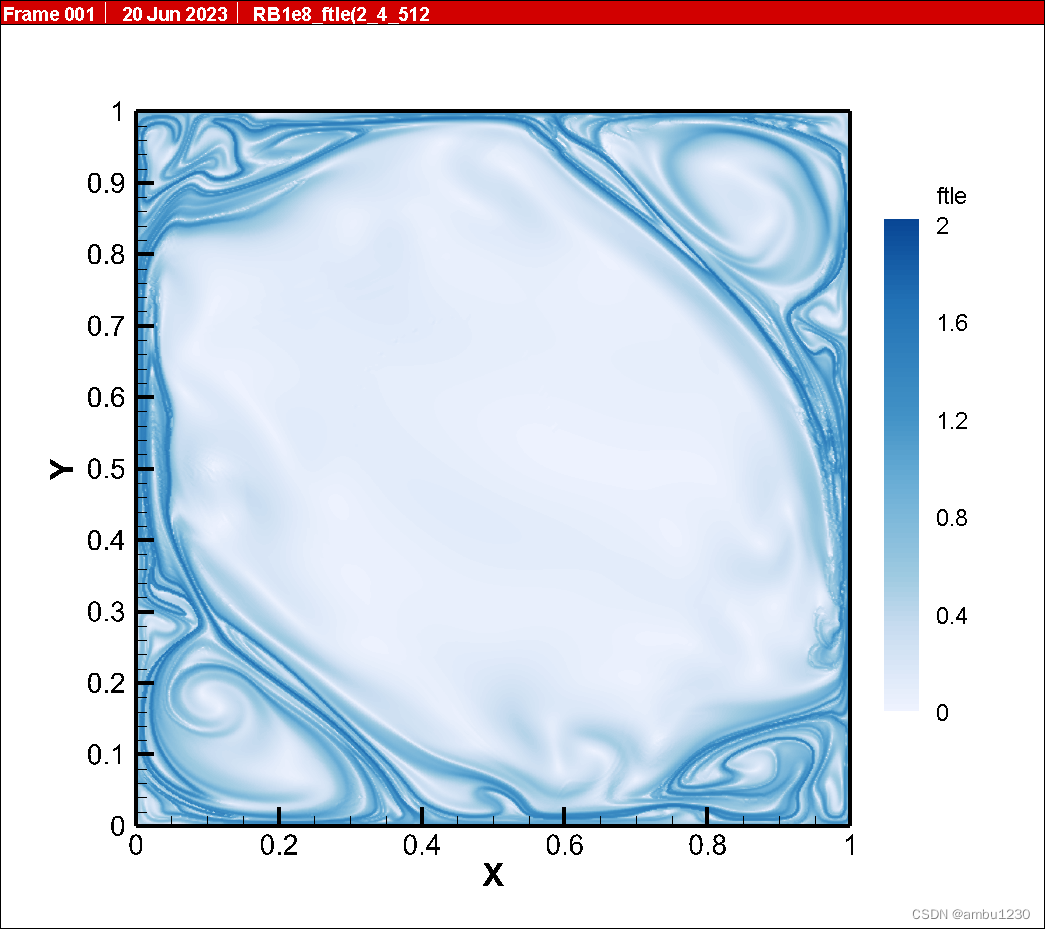
粒子数600600 如下:
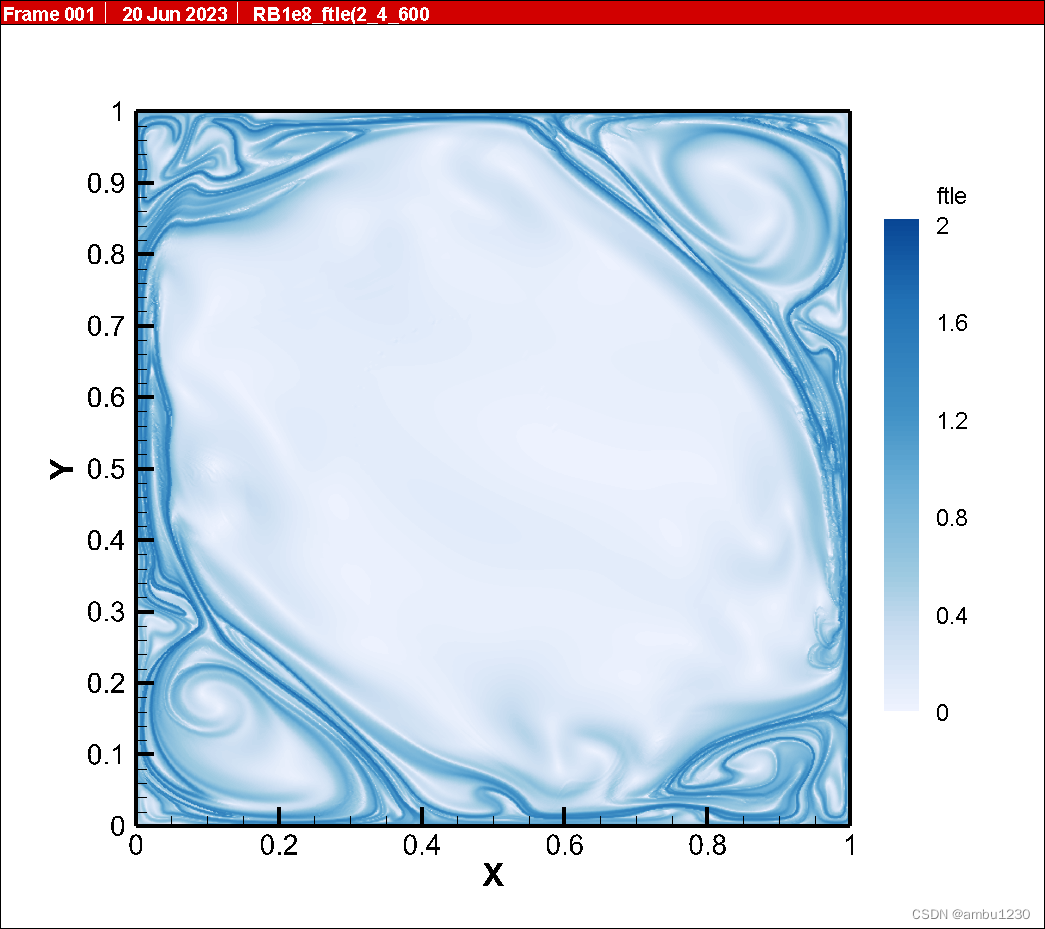
粒子数700700 如下(即第二张图):
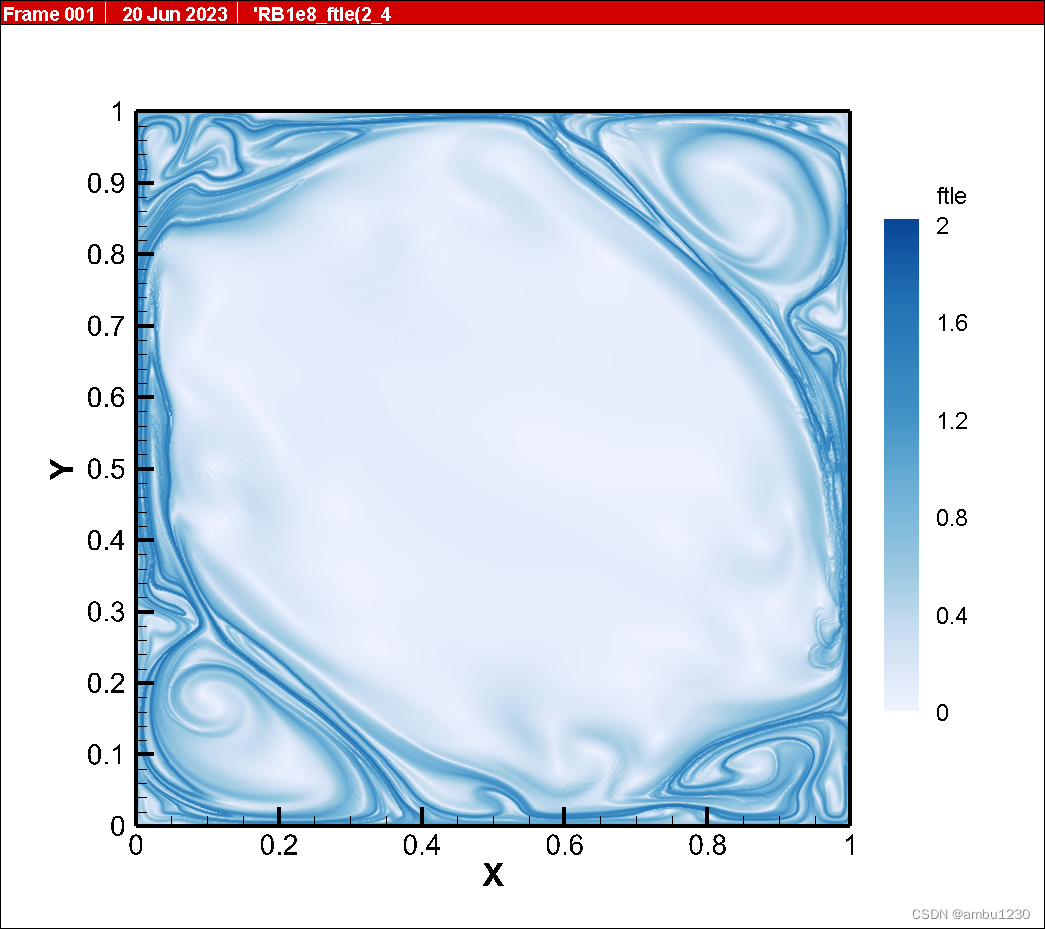
可以看出,随着粒子数的增加,其实变化不大,这里粒子数主要影响的是FTLE场的光滑程度,如果粒子太少,可以明显看出场中许多粗糙的地方。我额外做了一组
粒子数:256*256,结果如下图
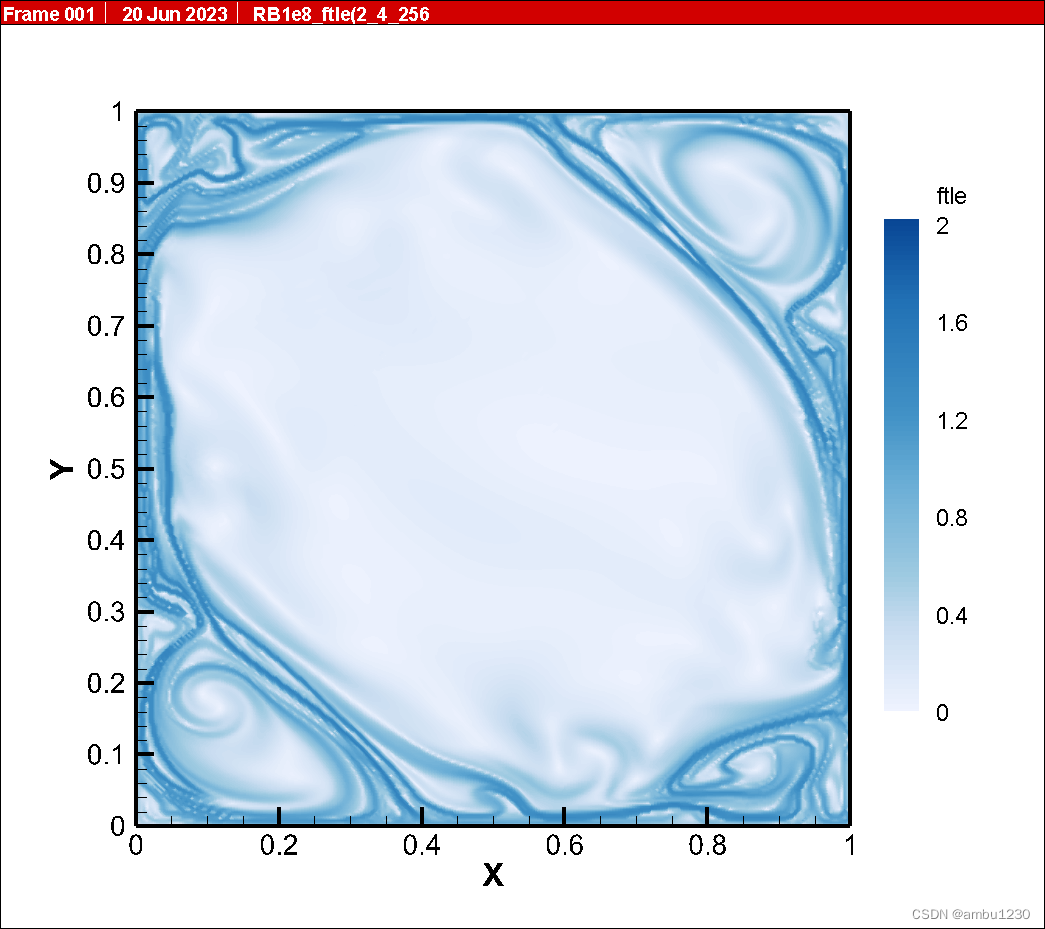
可以明显看出分辨率下降。
4、流场数据时间间隔的影响
流场数据的时间间隔直接决定了粒子追踪的精度。
这里我们对比dt = 0.1s和dt = 0.05s的结果
注意,上面展示的都是基于dt=0.05s的结果。
这部分我们依然固定FTLE(2),,积分时间:4s,粒子数固定为512*512;
dt = 0.1的结果,如下图:
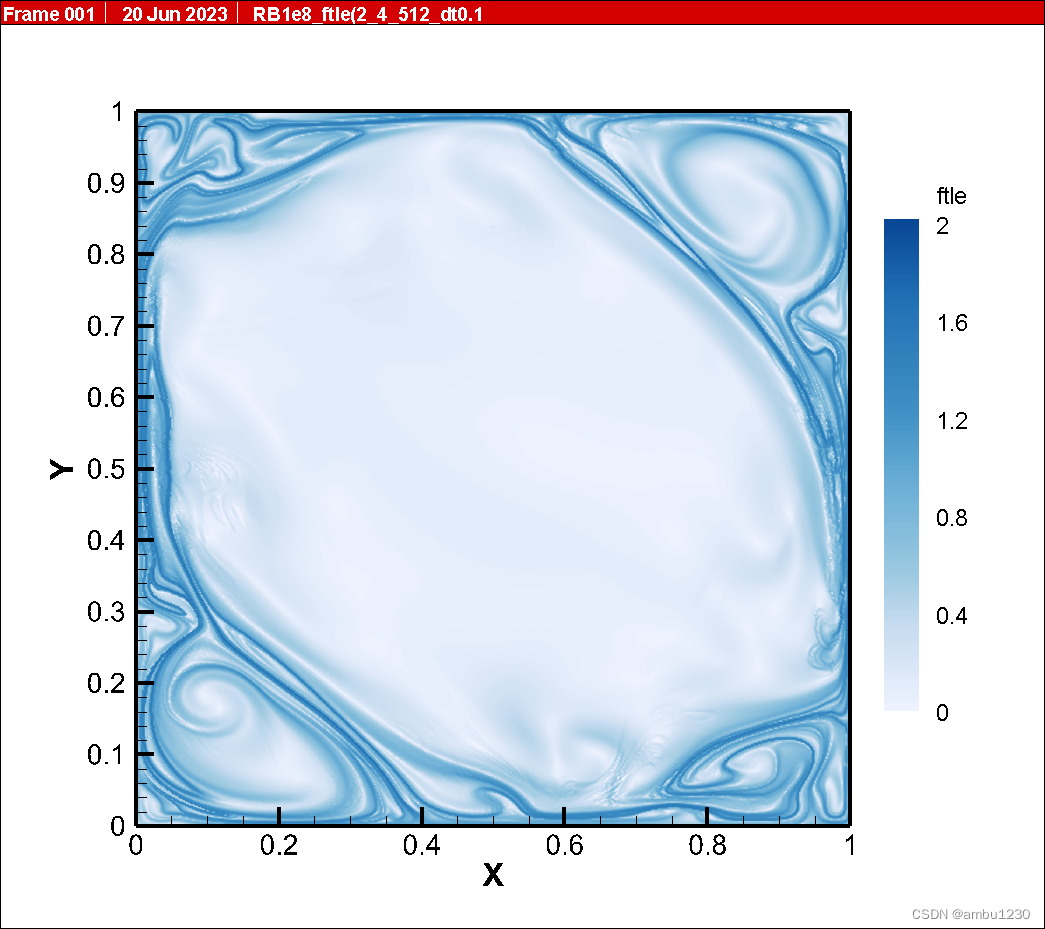
dt=0.05的结果(依然是第二幅图),如下图:
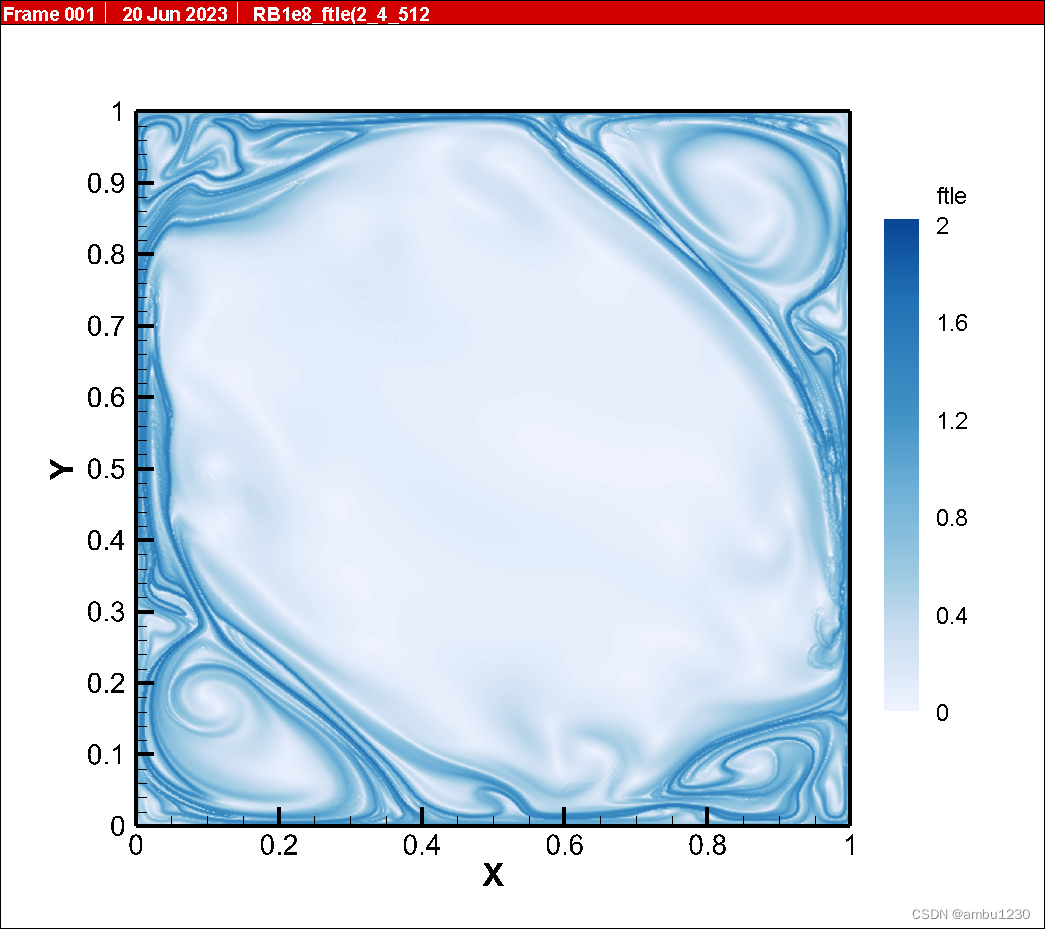
好吧,其实dt=0.1s的结果还说的过去,我本来以为会很差的,结果基本上跟dt=0.05s是一致的,可以看出我编写的粒子追踪的程序精度还是可以的。那以后就按dt=0.1s算吧这样节省了一倍的内存。
5、提取LCS结构
最后的最后,我们在来讨论一下从FTLE场提取LCS结构,即拉格朗日脊。
这里主要有两种方法,我们就拿dt-0.1;FTLE(2),积分时间4s,粒子数目512*512的结果来讨论吧。
5.1 shadden方法
该方法是由shadden提出的。
简单粗暴。
F
T
L
E
>
c
FTLE>c
FTLE>c
所有大于c的网格处的保留,其余的赋,即可得到LCS结构,其实我们的直觉也差不多是这样。
这个主要是根据经验需要调个参,但是效果其实还行。
下图是按这种方法提取的
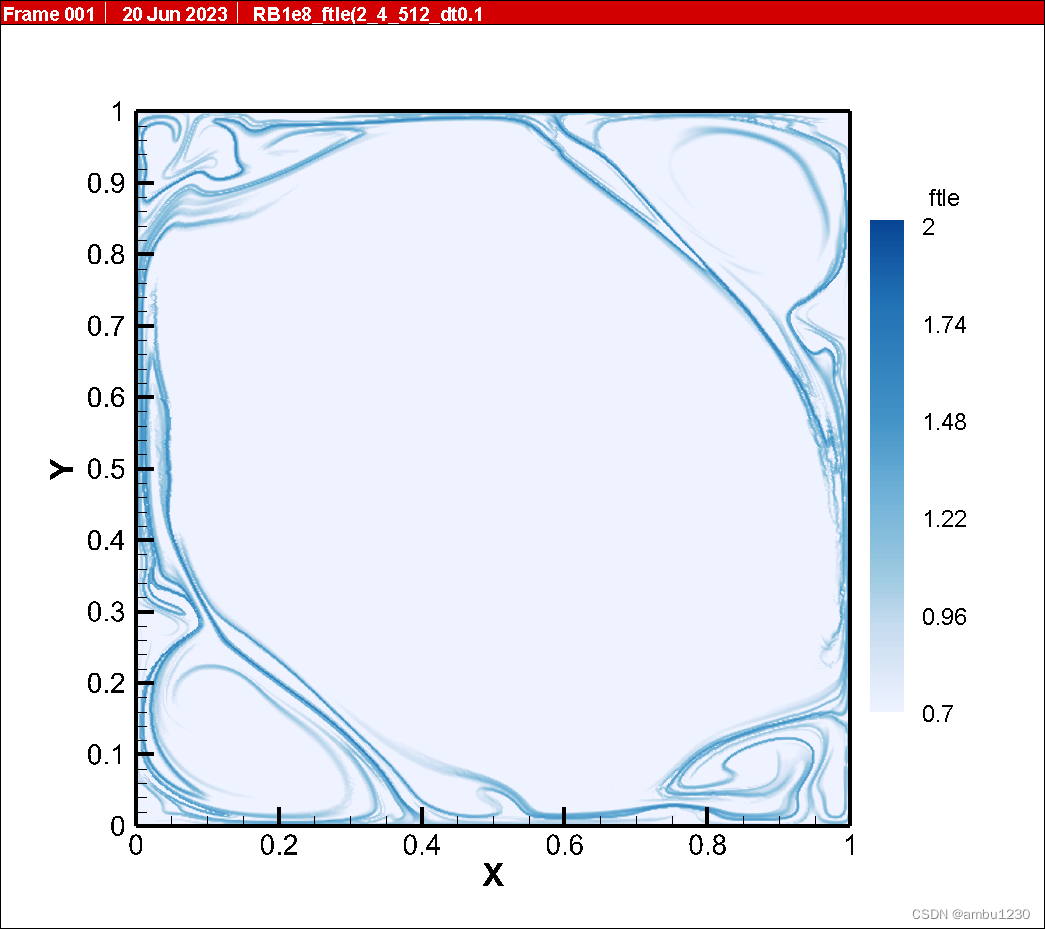
5.1 文献方法
F
T
L
E
(
x
,
y
)
−
⟨
F
T
L
E
⟩
x
>
c
F
T
L
E
r
.
m
.
s
.
.
\mathrm{FTLE}(x,y)-\langle\mathrm{FTLE}\rangle_x>c\mathrm{FTLE}_{r.m.s.}.
FTLE(x,y)−⟨FTLE⟩x>cFTLEr.m.s..
也有个参数需要调,但是这里人家告诉你了,c=1,2时结果还行,至少在文献中。
并且放了一张对比图。
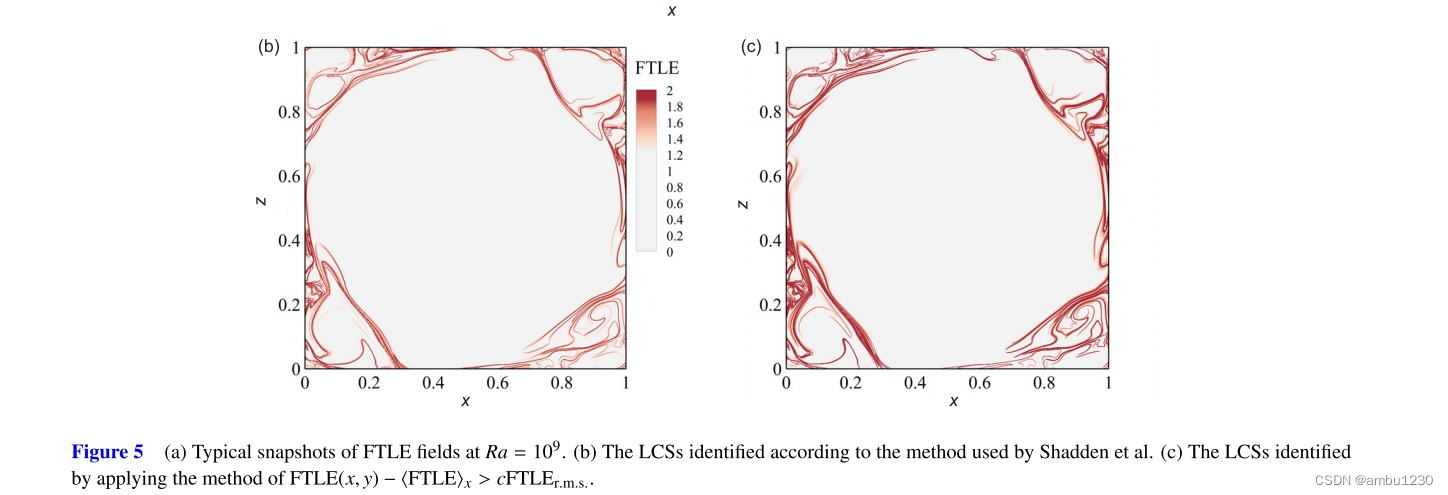
可以看出也确实还行。但是我对此图表示怀疑。因为文章下面的图就不是这样的了。
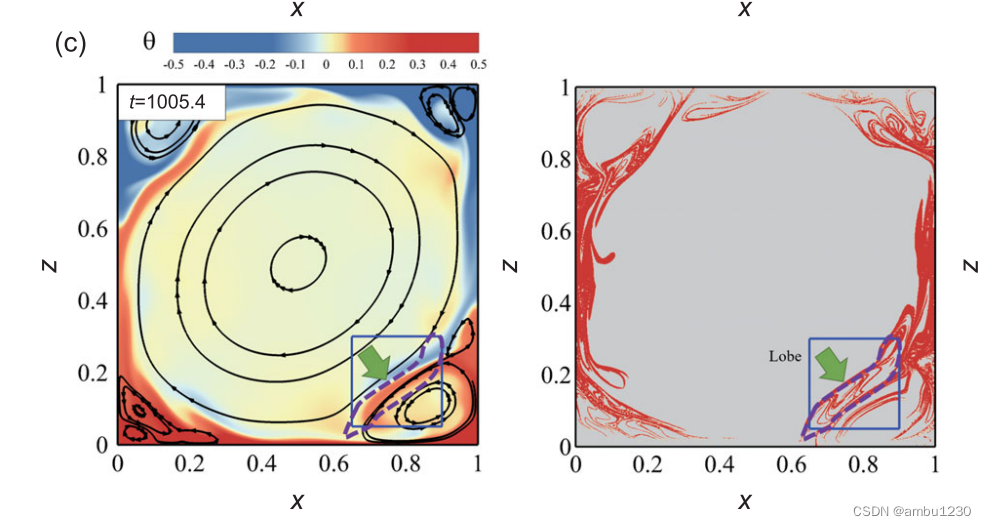
可以看出,明显侧壁的结构要粗很多,并且上下壁面也感觉有些缺失,这是因为与该课题组另一篇文章中的结果差别比较大。
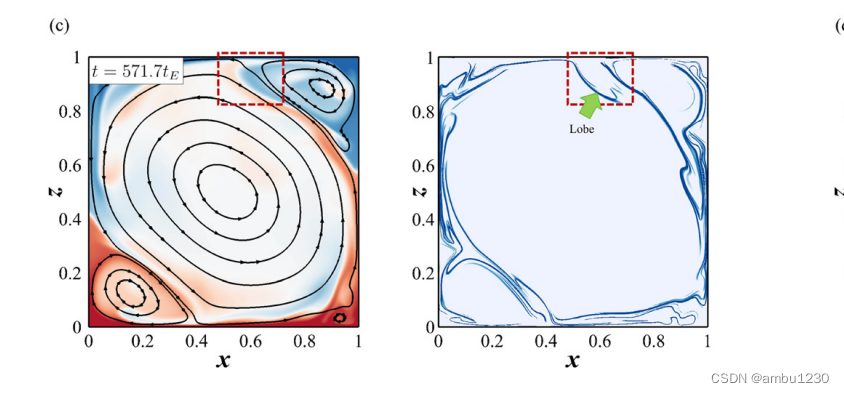
上下两幅图仅有流场Pr一个是0.7,一个是1,其实对流场的影响不大,但是由同样的方法提取处的LCS差距却着实比较大,明显后一个要更好一点。
下面来看看我利用该方法提取的LCS.(c=0.7)
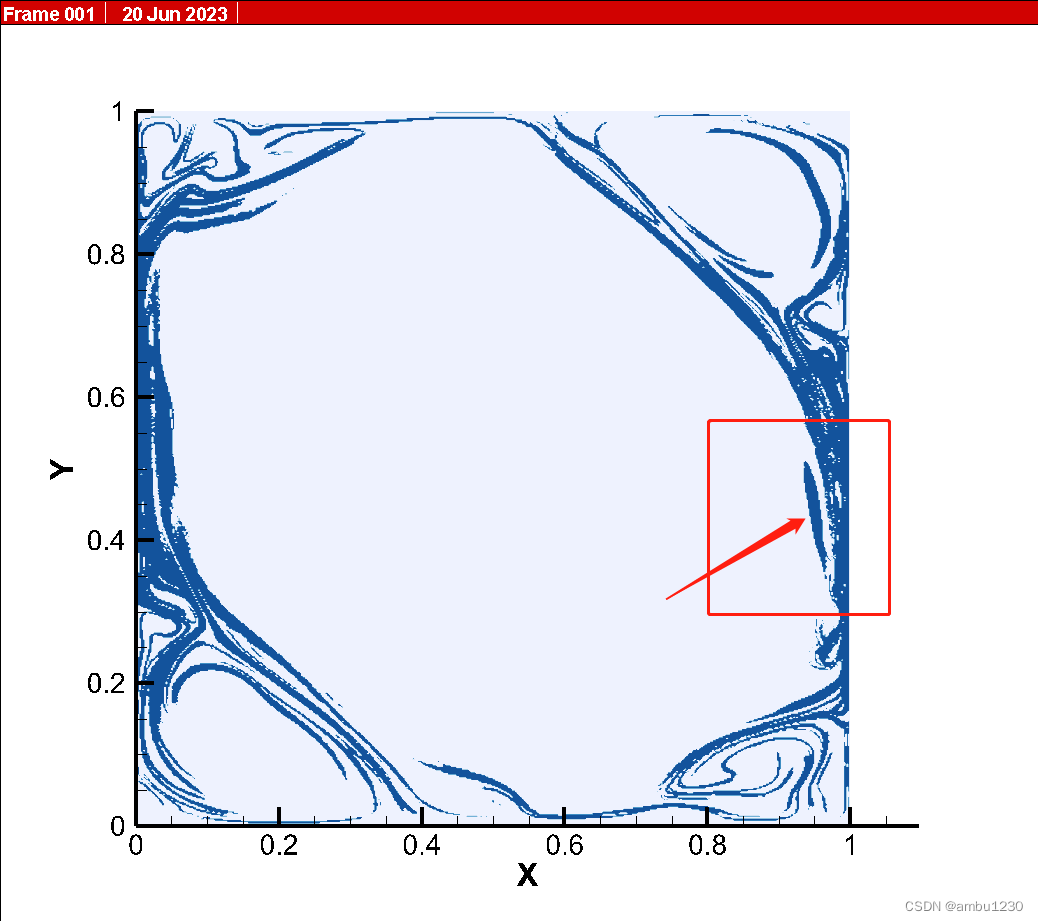
怎么说呢,我感觉是有问题的,侧壁明显多了一些FTLE场中看不出的结果。
我们来分析一下他这个方法,大于rms这一项没毛病,其实可以把这一项看成c也无妨,问题主要是在
⟨
F
T
L
E
⟩
x
\langle\mathrm{FTLE}\rangle_x
⟨FTLE⟩x,这个项上。
我的理解是在x方向的平均,也就是对于每个高度Y,取切片的平均,但是问题在于,FTLE场明显可以看出,中间高度位置处的FTLE平均明显是要小的,我们可以绘制
⟨
F
T
L
E
⟩
x
\langle\mathrm{FTLE}\rangle_x
⟨FTLE⟩x沿高度的变化。
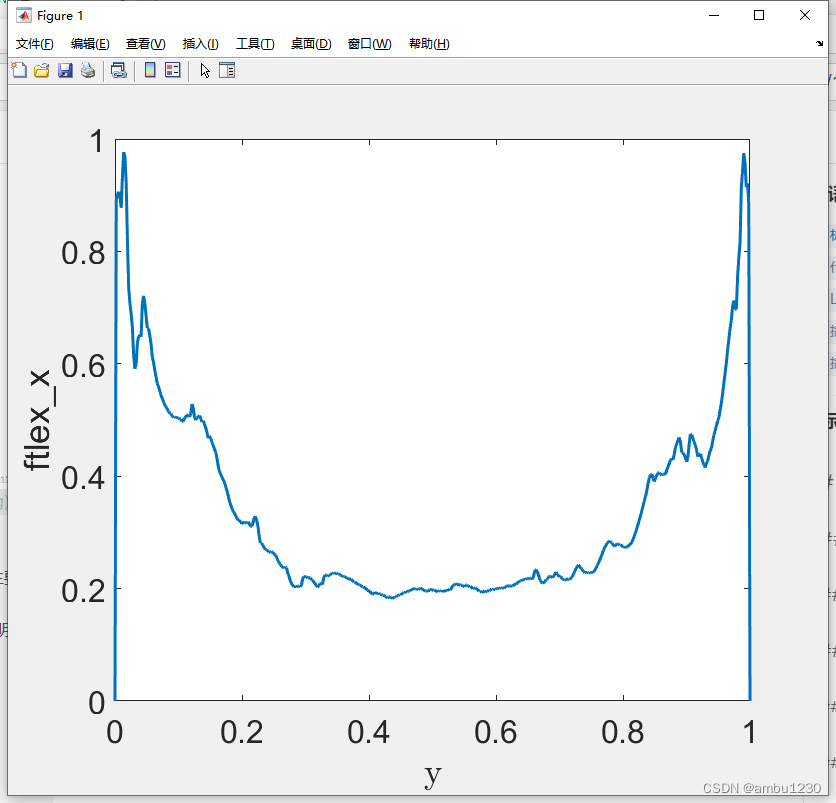
确实是这样,那么在计算时,侧壁处的将会更容易被识别成LCS.。。。
所以造成了这种情况。我们当然可以提高c值。c=1.2时,即文献中的值时结果如下
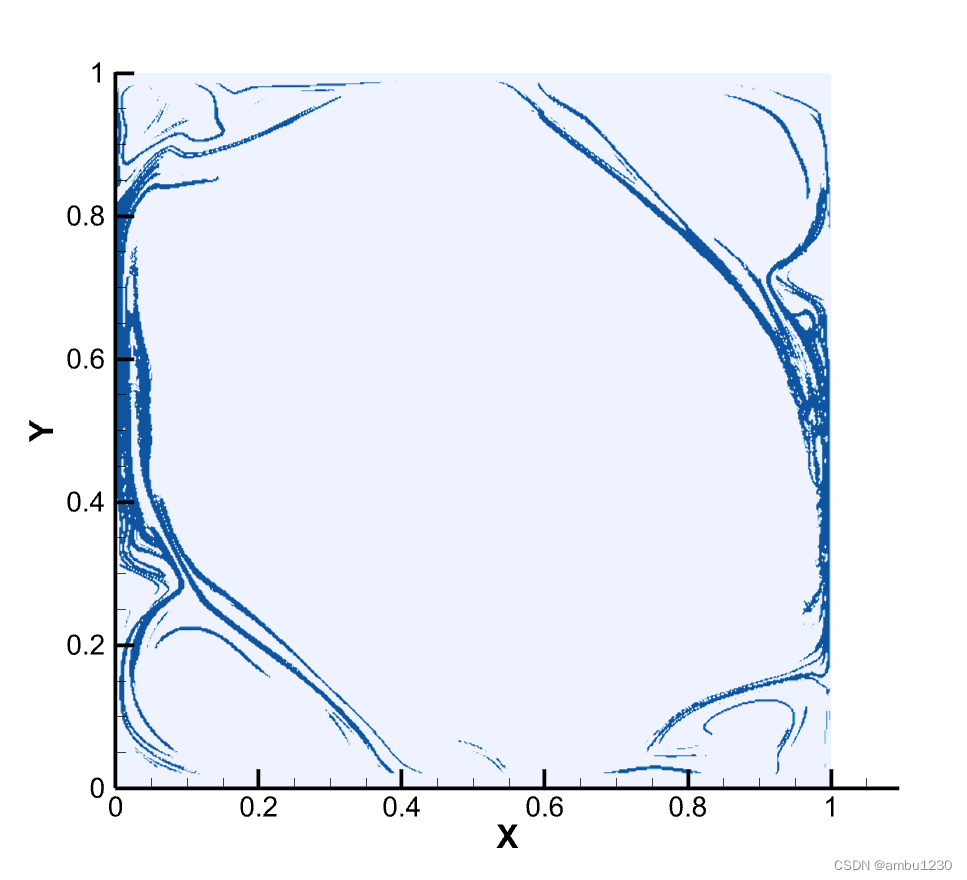
可以看出,上下边界处的一些结果是被忽略掉的。这里我不知道是不是我理解有问题,反正确定怪怪的,这种方法。
插一句,如果我理解的x坐标和他的不一样,即我试了一下在y方向取平均的结果
结果是,平均场的分布是类似的,都是中间小,两头大。
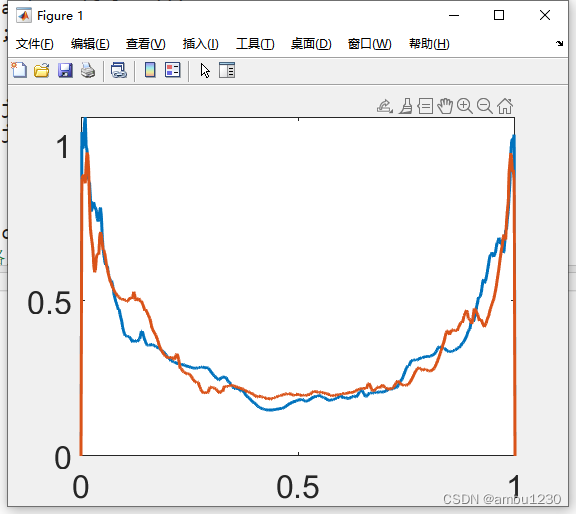
并且提取的结果上下壁面会变多,侧壁会变少
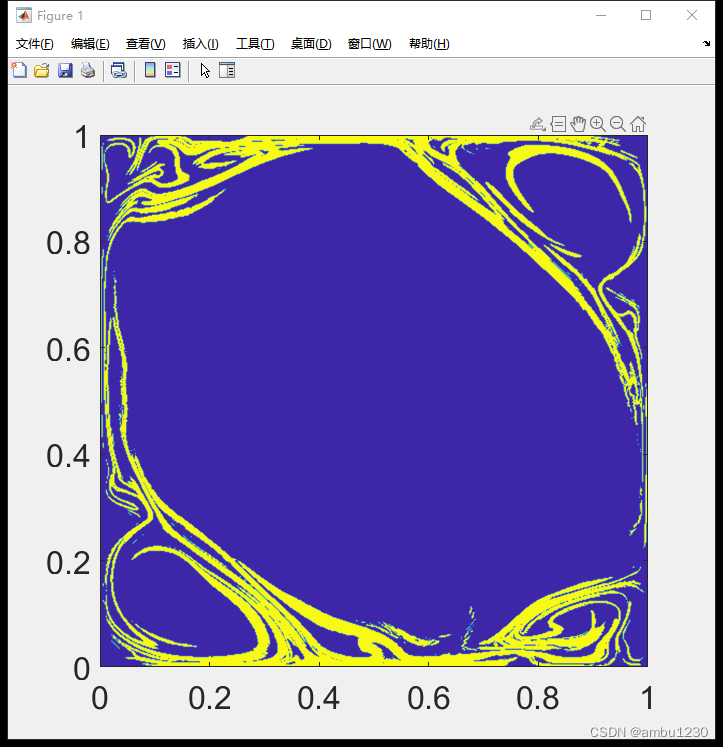
对此,我很怀疑

这种方法能提取出这种结构,但是好像确实这个上下壁面有缺失。
哎呀。。。好烦。。。
感觉还是第一种更加使用,不知道这个单方向求平均的意义在哪。。。