这是大模型系列模型的文章，针对《Knowledge Distillation of Large Language Models》的翻译。

摘要

知识蒸馏（KD）是一种很有前途的技术，可以减少大型语言模型（LLM）的高计算需求。然而，以前的KD方法主要应用于白盒分类模型或训练小模型来模仿像ChatGPT这样的黑盒模型API。如何有效地从白盒生成LLM中提取知识仍有待探索，随着LLM的蓬勃发展，这一点变得越来越重要。在这项工作中，我们提出了MINILLM，它从生成的较大语言模型中提取较小的语言模型。我们首先将标准KD方法中的前向Kullback-Leibler散度（KLD）目标替换为更适合生成语言模型上的KD的反向KLD，以防止学生模型高估教师分布的低概率区域。然后，我们推导出一种有效的优化方法来学习这个目标。在指令跟随设置中的大量实验表明，MINILLM模型生成更精确的响应，具有更高的整体质量、更低的曝光偏差、更好的校准和更高的长文本生成性能。我们的方法也适用于具有120M到13B参数的不同模型族。我们将在https://aka.ms/MiniLLM发布我们的代码和模型检查点。

1 引言

随着大型语言模型（LLM；$HZ{D}^{+}$，$BH{A}^{+}$，$BM{R}^{+}$，Ope，$CN{D}^{+}$）的快速发展，减少高计算资源需求的一种常见技术是知识蒸馏（KD；HVD），在这种技术中，我们在大型教师模型的监督下训练小学生模型。通常应用两类KD：黑盒KD和白盒KD，其中只有教师预测是可访问的，其中教师参数可供使用[JBMD]。最近，黑盒KD在对LLM API[$TG{Z}^{+}$，$CL{L}^{+}$，$WW{Z}^{+}$，$PL{H}^{+}$]生成的提示响应对的小模型进行微调方面显示出了有希望的结果。随着更多开源LLM[$ZR{G}^{+}$，$TL{I}^{+}$]的出现，白盒KD对研究界和行业部门都变得更有价值，因为学生模型从白盒教师模型中接收到更好的信号，从而可能带来更高的性能。然而，白盒KD方法主要用于小（<1B参数）语言理解模型[SDCW，$WW{D}^{+}$]，而用于生成LLM的白盒KD尚待探索。
在这项工作中，我们研究了LLM的白盒KD。我们认为，标准KD目标[KR16，$SS{T}^{+}$]对于以生成方式执行任务的LLM来说是次优的。给定由$\theta$参数化的教师分布$p(y|x)$和学生分布$q_{\theta }(y|x)$，标准KD目标（包括序列级模型的几个变体）本质上最小化了教师和学生分布之间的近似前向Kullback-Leibler散度（KLD），称为$KL[p||q_{\theta }]$，这迫使$p$覆盖$q_{\theta }$的所有模式。对于文本分类任务，$KL[p||q_{\theta }]$工作得很好，因为输出空间通常由有限个类组成，使得$p(y|x)$和$q_{\theta }(y|x)$都有几个模式。然而，对于开放文本生成任务，其中输出空间要复杂得多，并且由于模型容量有限，$p(y|x)$可以包含比$q_{\theta }(y|x)$所能表达的模式多得多的模式。最小化正向KLD可能导致$q_{\theta }$将不合理的高概率分配给$p$[MG]的空位区域，并在自由运行生成期间在$p$下产生非常不可能的样本[Hus]。

为了缓解这个问题，我们建议最小化反向KLD，$KL[q_{\theta }||p]$，它被广泛用于计算机视觉[KW]和强化学习[$CP{O}^{+}$]。与$KL[p||q_{\theta }]$相比，最小化$KL[q_{\theta }||p]$会导致$q_{\theta }$寻找$p$的主要模式，并将低概率分配给$p$的空穴区域[$M^{+}$]，如第2.1节中的试点实验所示。在LLM的语言生成中，这意味着学生模型避免学习太多教师分布的长尾变体[$HB{D}^{+}$]，并关注生成的响应的正确性，这在需要真实性和可靠性的实际场景中至关重要[$JL{F}^{+}$]。如第2.2节所示，为了优化${\min }_{\theta }KL[q_{\theta }||p]$，我们用策略梯度[SSMSM]推导目标的梯度。尽管最近的工作表明，通过策略优化在微调PLM方面取得了成功[$OW{J}^{+}$，$RA{B}^{+}$]，但我们发现，训练模型仍然存在高方差、奖励黑客和生成长度偏差。因此，我们引入了（1）单步正则化来减少方差，（2）教师混合采样来缓解奖励黑客行为，以及（3）长度归一化来消除长度偏差。最后，我们在第2.3节中介绍了MINLLM的算法。
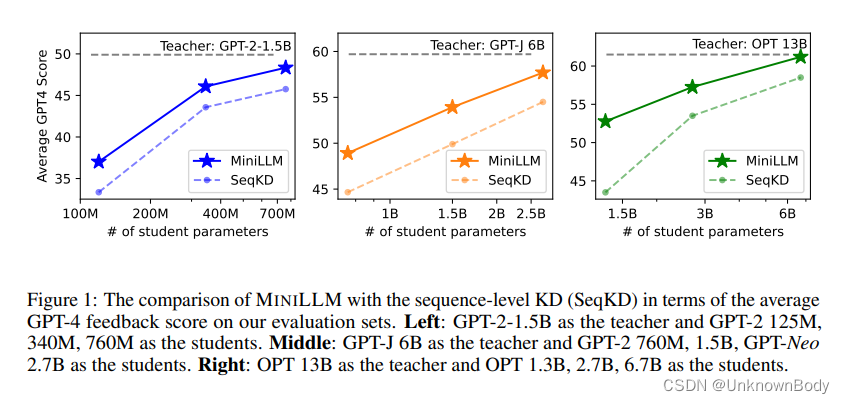
我们将MINLLM应用于各种生成语言模型[$RW{C}^{+}$，$ZR{G}^{+}$，$TL{I}^{+}$]，参数大小范围从120M到13B，在指令跟随设置[$SW{R}^{+}$，$WB{Z}^{+}$]中，该设置涵盖了大量的NLP任务。我们使用五个具有GPT-4反馈和Rouge-L[Lin]的指令跟随数据集进行评估。我们的实验表明，MINILM在所有数据集上始终优于标准KD基线，并从120M模型扩展到13B模型（见图1）。更多的分析表明，MINILLM具有更低的曝光偏差、更好的校准，并且在产生具有更好多样性的长响应方面表现更好。

2 方法

我们考虑条件语言生成任务，其中模型在从分布$p_x$采样的提示$x$上产生响应 y = { y t } t = 1 T y=\{y_t\}^{T}_{t=1} y={yt​}t=1T​。我们将KD公式化为一个优化问题，以最小化固定的教师模型分布$p(y|x)$和由$\theta$参数化的学生模型分布$q_{\theta }(y|x)$之间的差异。生成模型的标准KD近似最小化前向KLD$KL[p||q_{\theta }]={\mathbb{E}}_{x\sim p_x,y\sim p^{\prime }}\log \frac{p(y|x)}{q_{\theta }(y|x)}$，其中$p^{\prime }$可以是真实数据分布（单词级KD）或教师分布$p$（序列级KD）。尽管$KL[p||q_{\theta }]$被广泛使用，但当$q_{\theta }$不足以覆盖$p^{\prime }$[$JK{H}^{+}$]的所有模式时，它已经被证明在语言生成任务中高估了$p$的空位区域。LLM的KD适合这种情况，因为LLM以生成的方式执行各种任务，使得低能力的学生模型不能完美地模仿教师模型或人类的复杂语言生成分布。

2.1 MiniLLM：利用逆向KLD进行知识蒸馏

在这项工作中，我们将最小化学生和教师分布之间的反向KLD作为MINILLM的学习目标：
$$\begin{array}{c}\theta =\underset{\theta }{\mathrm{argmin}}\mathcal{J}(\theta )=\underset{\theta }{\mathrm{argmin}}KL[q_{\theta }||p]\\ =\underset{\theta }{\mathrm{argmin}}{\mathbb{E}}_{x\sim p_x,y\sim q_{\theta }}\log \frac{q_{\theta }(y|x)}{p(y|x)}.\end{array}$$
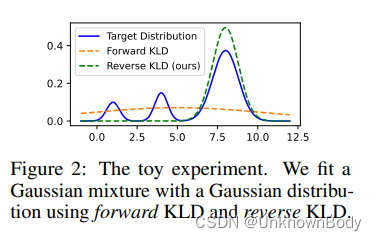
[Hus]已经表明，最小化$KL[q_{\theta }||p]$会导致模式搜索行为，其中$q_{\theta }$将高概率分配给$p$的大模式，而忽略小模式。图2说明了当高斯分布试图拟合高斯混合时，两个KLD之间的差异。我们可以看到，最小化正向KLD导致$q_{\theta }$在$p$的零概率位置上放置大概率质量，这对应于实践中低质量文本的生成，而反向KLD关注$p$的主要模式，这对于确保语言生成的正确性和忠实性至关重要。
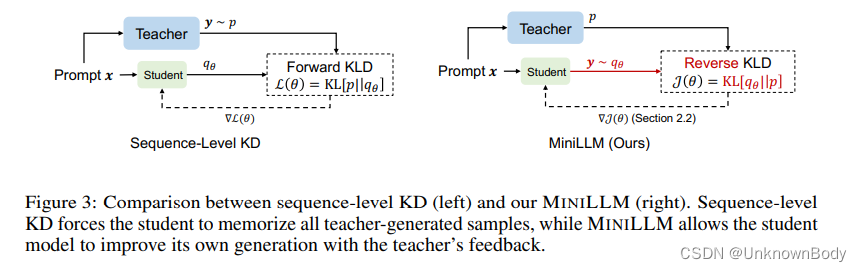
我们通过最小化反向KLD将LLM的KD方法称为MINILLM，如图3所示。与序列级KD不同，MINILLM并不强制$q_{\theta }$拟合从教师分布$p$中采样的所有$y$。相反，它鼓励学生在自己的能力范围内生成教师喜欢的样本，这更可能实现。

2.2 策略梯度优化

梯度推导
我们注意到，方程（1）中描述的目标函数$\mathcal{J}(\theta )$的梯度可以使用策略梯度定理[Wil，HTAL]推导：
$$\begin{array}{c}\nabla \mathcal{J}(\theta )=-{\mathbb{E}}_{y\sim q_{\theta }(\cdot |x)}\sum _{t=1}^T(R_t-1)\nabla {\log }_{q_{\theta }}(y_t|y_t,x).\end{array}$$
其中，$T=|y|$和$R_t={\sum }_{t^{\prime }=t}^T\log \frac{p(y_{t^{\prime }}|y_{<t^{\prime }},x)}{q_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)}$是度量每个步骤生成的质量的$r_{t^{\prime }}=\log \frac{p(y_{t^{\prime }}|y_{<t^{\prime }},x)}{q_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)}$的累积。直观地说，我们希望在教师分布下，通过增加$p(y_{t^{\prime }}|y_{<t^{\prime }},x)$使生成具有高概率，但同时通过降低$q_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)$保持多样性。期望值是通过蒙特卡罗抽样计算的。然而，策略梯度受到高方差和奖励黑客攻击的影响。尽管随后的工作提出了更好的解决方案，如PPO，但我们发现这些问题仍然存在。此外，我们注意到$R_t$倾向于短句，这导致我们的模型输出空的响应。因此，我们提出了三种策略来缓解这些问题。
单步正则化
[$CP{O}^{+}$]发现，单步生成质量$r_t$对训练方差至关重要，因为前面标记中的误差沿着整个句子累积。为了更多地关注$r_t$，我们重写了$\mathcal{J}(\theta )$以将$r_t$从$R_t$中分离出来，并直接计算${\mathbb{E}}_{y_t\sim q_{\theta }(t)}[r_t]$的梯度作为正则化（完整推导见附录a.2）：
$$\begin{array}{c}\nabla \mathcal{J}(\theta )={\mathbb{E}}_{y\sim q_{\theta }(\cdot |x)}[-\sum _{t=1}^T{R}_{t+1}\nabla \log q_{\theta }(y_t|y_{<t},x)]+{\mathbb{E}}_{y\sim q_{\theta }(\cdot |x)}[-\sum _{t=1}^T\nabla {\mathbb{E}}_{y_t\sim q_{\theta }(t)}[r_t]]\\ =(\nabla \mathcal{J}{)}_{Main}+(\nabla \mathcal{J}{)}_{Reg},\end{array}$$
其中$q_{\theta }(t)=q_{\theta }(\cdot |y_{<t},x)$。注意，${\mathbb{E}}_{y_t\sim q_{\theta }(t)}[r_t]$可以通过在词汇表上求和而不是使用蒙特卡罗采样来直接计算，并且可以相对于$\theta$导出。这种正则化给出了对单步生成质量的更精确和有效的估计，这减少了训练过程中的方差并加速了收敛。
教师混合抽样
我们在使用等式2进行训练时观察到奖励黑客，因为$q_{\theta }$有时会产生退化句子$y$，在抽样过程中从教师那里获得高分（例如，重复短语），尤其是对于小型学生模型。为了创建更好的抽样分布，我们在每个时间步长混合教师和学生的分布：
$$\begin{array}{c}\tilde{p}(y_t|y_{<t},x)=\alpha \cdot p(y_t|y_{<t},x)+(1-\alpha )\cdot q_{\theta }(y_t|y_{<t},x)\end{array}$$
其中$\alpha$控制教师混合的强度。在老师的帮助下从$\tilde{p}$采样抑制了低质量的生成，并缓解了奖励黑客行为。我们用重要性采样重写$(\nabla \mathcal{J}{)}_{Main}$和$(\nabla \mathcal{J}{)}_{Reg}$，以得到梯度的无偏估计量：
$$\begin{array}{c}(\nabla \mathcal{J}{)}_{Main}=-{\mathbb{E}}_{y\sim \tilde{p}(\cdot |x)}\sum _{t=1}^T{w}_t{R}_{t+1}\nabla \log q_{\theta }(y_t|y_{<t},x),\\ (\nabla \mathcal{J}{)}_{Reg}=-{\mathbb{E}}_{y\sim \tilde{p}(\cdot |x)}[\sum _{t=1}^T{w}_t\nabla {\mathbb{E}}_{y_t\sim q_{\theta }(t)}[r_t]],\end{array}$$
其中$w_t={\prod }_{t^{\prime }=1}^t\frac{q_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)}{{\tilde{p}}_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)}$是重要性参数。然而，在实践中，已经发现使用$w_t$对超参数敏感并且收敛缓慢。因此，我们近似地设置$w_t\approx \frac{q_{\theta }(y_t|y_{<t},x)}{{\tilde{p}}_{\theta }(y_t|y_{<t},x)}$以减少方程5中估计器的方差。
长度归一化
我们发现，长序列往往具有较小的$R_{t+1}$，这鼓励模型产生短响应。因此，我们将长度归一化添加到等式3中的$R_{t+1}$：
$$\begin{array}{c}{R}_{t+1}^{Norm}=\frac{1}{T-t-1}\sum _{t^{\prime }=t+1}^T\log \frac{p(y_{t^{\prime }}|y_{<t^{\prime }},x)}{q_{\theta }(y_{t^{\prime }}|y_{<t^{\prime }},x)}\end{array}$$
总之，结合以上列出的策略，我们得到了最终的优化梯度：
$$\begin{array}{c}\nabla \mathcal{J}(\theta )=-{\mathbb{E}}_{y\sim \tilde{p}(\cdot |x)}\left[\sum _{t=1}^T{w}_t\right[R_{t+1}^{Norm}\frac{\nabla q_{\theta }(y_t|y_{<t},x)}{q_{\theta }(y_t|y_{<t},x)}+\nabla \sum _{y/\in V}{q}_{\theta }(y^{\prime }|y_{<t},x)\log \frac{p(y^{\prime }|y_{<t},x)}{q_{\theta }(y^{\prime }|y_{<t},x)}]],\end{array}$$
其中$V$是语言模型的词汇表大小。

2.3 训练算法

MINLLM的训练算法如算法2.3所示。我们从对具有最低验证损失的训练数据进行微调的检查点初始化学生模型，并将PPO裁剪策略添加到$(\nabla \mathcal{J}{)}_{Main}$以提高训练稳定性。注意，我们没有在PPO中使用值网络和KL正则化来提高训练效率。与[$OW{J}^{+}$]相同，我们在预训练语料库上添加了语言建模损失${\mathcal{L}}_{PT}$。

3 实验

3.1 实验设置

我们通过首先在教学响应数据集$\mathcal{D}$上微调一个大模型作为教师$p$来进行实验。然后，我们比较了不同的KD方法，通过评估蒸馏模型的指令跟随性能，在教师的指导下蒸馏$\mathcal{D}$上的一个较小的学生模型。
基础模型
我们提取了三种不同大小的模型：GPT-2（120M、340M、760M）、OPT（1.3B、2.7B、6.7B）和LLaMA（7B），分别使用GPT-2-1.5B、OPT13B和LLaMA-13B作为每种模型类型的教师。我们还在附录C.1中介绍了使用GPT-J作为教师的结果。
训练
我们从由15K人写指令-响应对组成的databricks-doolly-15k构建训练数据。我们随机分割14K个样本作为训练集$\mathcal{D}$，并分别留下500个样本进行验证和测试。对于${\mathcal{D}}_{PT}$，我们对GPT-2家族使用OpenWebText，对其他模型使用RoBERTa训练语料库。在整个实验中，我们将教师的混合强度设定为$\alpha =0.2$。我们在验证集上使用Rouge-L分数来选择超参数，因为它比验证损失更符合人类偏好。更多训练细节见附录B.1。
评估
我们在以下五个指令数据集上评估训练后的模型：

• DollyEval：我们从databricks-dolly-15k数据集中分离出的500个样本测试集。
• SelfInst：一个面向用户的指令集，包含252个样本。
• VicunaEval：Vicuna评价中使用的80个具有挑战性的问题。
• S-NI：SUPER-NATURALINSTRUCTIONS的测试集，由119项任务中的9K个样本组成。在[$PL{H}^{+}$]之后，我们将集合划分为3个子集，其基本事实响应长度分别为[0，5]、[6，10]和[11，$+\infty$]。我们在第3.2节中使用[11，$+\infty$]子集，并在第3.3节中对所有子集进行分析。
• UnNI：UNNATURALINSTRUCTIONS的核心集合，包含60K个样本。与S-NI类似，我们首先对[11，$+\infty$]子集进行评估，然后对附录C.2中所有子集的性能进行分析。

我们采用两个指标来评估模型生成的响应：

• R-L：Rouge-L分数，用于衡量模型生成的精度。[$WM{A}^{+}$]已经表明，Rouge-L适合于大规模的教学跟踪评估。
• GPT4:GPT-4反馈，要求GPT-4将模型生成的回答与基本事实回答进行比较，并为两个回答提高1-10分（我们使用的提示见附录B.2）。我们报告了模型回答和基本事实回答的总分之比。此指标仅适用于DollyEval、SelfInst和VicunaEval。

对于所有测试集，我们对温度=1的响应进行采样，并报告具有不同随机种子的每个提示的5代的平均分数。
基线
我们在主要实验中考虑了三个基线：

• SFT w/o KD直接微调D上的学生模型，并用黄金响应进行监督。
• KD使用教师分布作为每个表征步骤的监督，对$\mathcal{D}$上的学生模型进行微调，也称为单词级KD。
• SeqKD根据教师生成的数据对学生模型进行微调。

3.2 结果

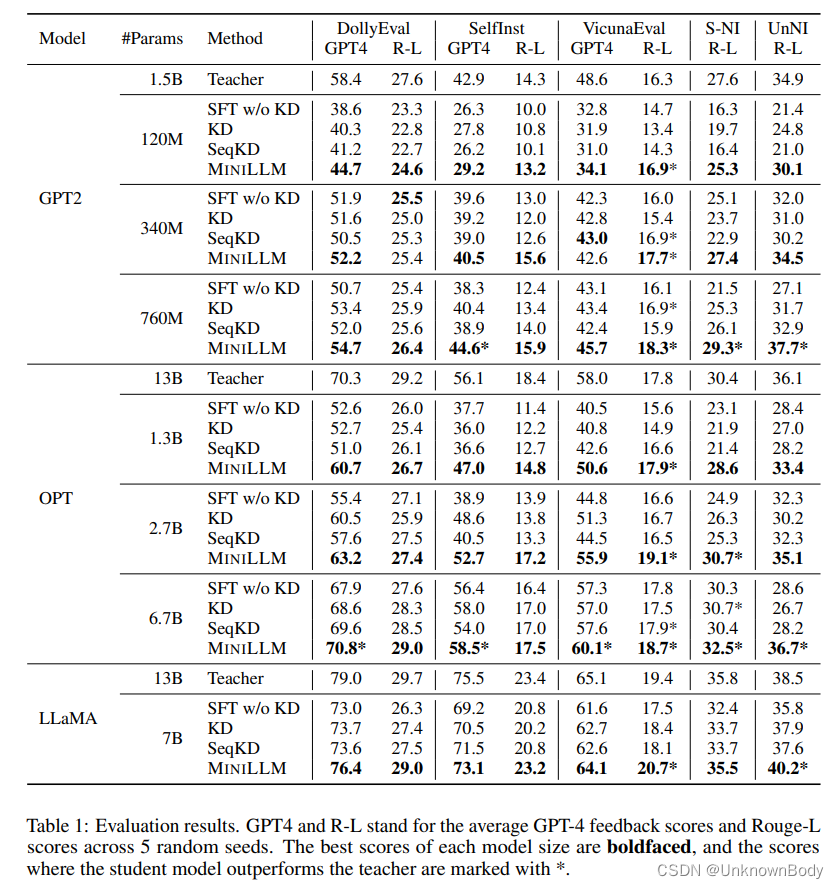
我们在表1中给出了评估结果，其中我们有四个观察结果。
首先，通过将SFT与近似最小化前向KLD的KD和SeqKD进行比较，我们可以看到，这些标准KD方法在大多数情况下成功地从教师模型中提取了知识，获得了更好的Rouge-L和GPT-4反馈分数，这重申了以前工作中的结论。
其次，通过将MINILLM的GPT-4反馈分数与基线进行比较，我们观察到，当使用不同的基础模型进行训练并在各种评估集上进行测试时，我们的方法提取的模型在几乎所有情况下都优于基线。这表明MINLLM是一种提取具有高整体性能的小型模型的通用方法。我们还发现，与基线相比，MINILLM在DollyEval以外的数据集上通常工作得更好，这表明我们的方法具有良好的分布外泛化能力。
第三，Rouge-L分数表明，MINILLM模型产生了与基本事实高度重叠的最精确的响应。我们注意到，在某些情况下，特别是在VicunaEval、S-NI和UnNI上，学生模型的Rouge-L分数比老师高，这与[$FL{T}^{+}$]中的观察结果相匹配。我们推测，原因是标准教师强制微调带来了教师训练推断差异，也称为暴露偏差。相反，MINILLM是用策略优化方法优化的，这减轻了曝光偏差。我们在第3.3节中对暴露偏差进行了进一步分析。
第四，比较模型尺寸和模型族的结果，我们可以看到，当三个模型族的基本模型尺寸在120M到13B之间变化时，MINILLM的改进是一致的。这一趋势也如图1所示，它展示了我们的方法在LLM时代的卓越可扩展性和通用性。

3.3 分析

暴露偏差
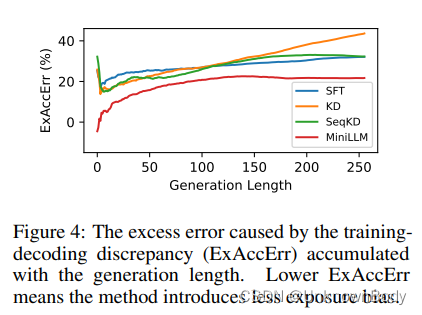
为最大限度地减少正向KLD而训练的语言生成模型已知存在暴露偏差，这是由教师强迫训练和自由生成之间的差异引起的。在MINILLM中，我们在训练阶段从学生模型中收集样本，这缓解了训练和评估之间的不匹配。在图4中，我们使用附录B.3中定义的ExAccErr度量来测量由于自回归解码中的暴露偏差导致的过度累积误差。实验以GPT-2-125M为基础，GPT-2-1.5B为教师，DollyEval为测试集。对于每个提示，我们对10个响应进行抽样，以减少方差。我们可以看到，微调模型的ExAccErr在生成过程中不断增长，而MiniLLM的ExAcc Err要低得多，并且对于长文本生成（>150个词元），错误停止累积。
校准
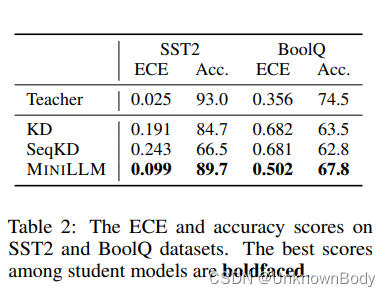
[Ope]已经表明，RL训练的模型可能校准得很差。基于LLaMA-7B模型，我们在两个广泛使用的文本分类数据集：SST2和BoolQ上测试了MINILLM和KD基线的校准。我们设计了零样本分类指令（见附录B.2），并采用标签词的概率来计算ECE得分。从图2可以看出，用KD和SeqKD训练的模型比教师模型校准得更差，这可能解释了它们在规范基准测试上的低性能。我们怀疑原因是最小化前向KLD导致模型将高概率推到目标分布的零概率点，这导致学生和教师之间的显著分布差异（见图2中的直观示例）。相比之下，MINILLM专注于准确地学习目标分布的主要部分，这缩小了学生和教师之间的ECE分数差距。


不同响应长度下的性能
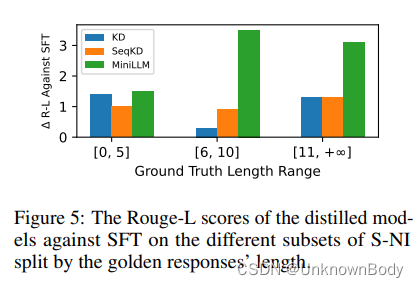
我们研究了当黄金响应长度属于不同范围时模型的性能。在图5中，我们展示了不同KD模型相对于SFT模型在三个S-NI子集上的Rouge-L得分，这些子集由基本事实响应的长度划分。我们可以看到，所有方法在预期短响应（≤5个标记）的提示上都获得了低分数，这可能是因为我们训练集中的大多数响应都是长句，这引入了训练和测试之间的分布变化。此外，这些提示的输出空间相对较小，允许学生模型覆盖教师的大多数模式，因此反向KLD和正向KLD具有相似的性能。对于响应较长（≥6个标记）的提示，由于输出空间复杂，教师分布包含的模式比学生多，这表明了MINILLM相对于标准KD方法的优势。UnNI的类似结果如附录C.2所示。
生成多样性
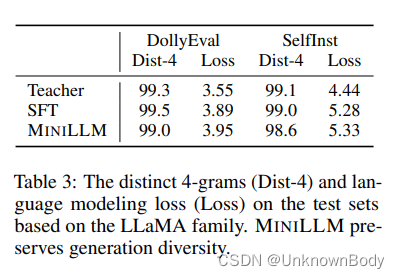
[$C{F}^{+}$]发现，通过最小化反向KLD优化的模型可能会丢失模式，从而影响生成多样性。我们遵循[PH]从三个方面讨论了生成多样性：（i）在给定提示的情况下生成多个不同的响应。（ii）产生语言上复杂的反应。（iii）生成具有真实数据分布的高覆盖率的内容的能力。对于（i），我们认为，对于许多NLP应用程序，生成一个正确的响应就足够了，尤其是对于那些要求高真实性和可靠性的场景。对于（ii）和（iii），我们使用LLaMA家族的基本模型，在表3中报告了测试集上回答的不同4-gram比例和语言建模损失。我们可以看到，MINILLM在生成的响应中保留了明显的4-gram比例，并且不会导致测试集上的语言建模损失增加太多。

3.4 消融实验

优化策略的影响
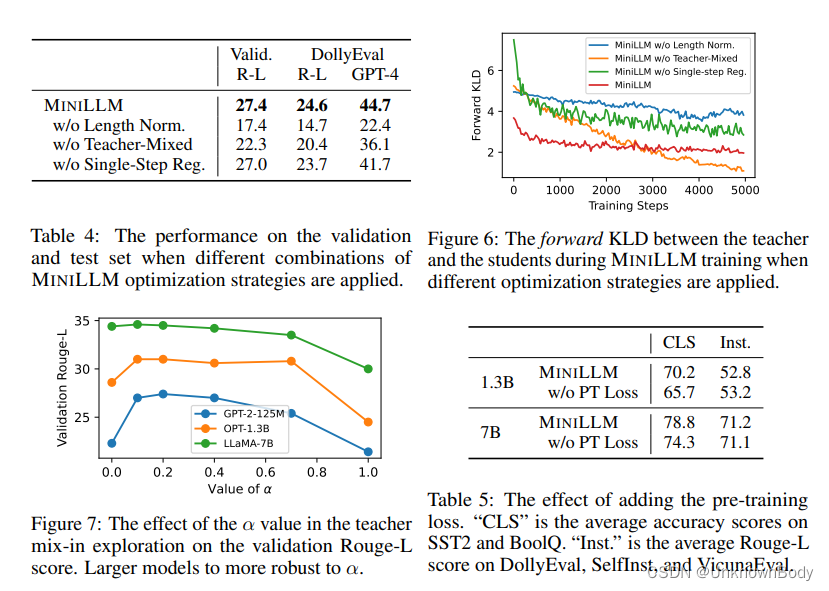
我们通过从GPT-2-1.5B模型中提取GPT-2-125M模型，对第2.2节中提出的稳定和加速优化的三种策略进行了消融研究。在表4中，我们报告了每次运行的验证集上的最佳Rouge-L分数以及相应检查点的评估结果。在图6中，我们还绘制了训练期间学生和老师之间的反向KLD，其中线被平滑了32步。我们可以看到，教师混合抽样和长度归一化对稳定训练至关重要。尽管在没有这些策略的情况下，反向KLD也会减少，但我们发现，模型很快学会生成在教师分布中具有高概率的重复、短或无意义的字符串（见附录D中的示例），这被称为奖励黑客。这也导致了表4中的低生成性能。从图6中，我们还观察到，单步正则化有效地减少了训练过程的方差，这也导致了验证和测试集的更高性能。
教师组合强度$\alpha$的影响
在图7中，我们使用GPT-2-1.5B、OPT-13B和LLaMA-13B作为教师，绘制了GPT-2-125M、OPT-1.3B和LLaMA-7B验证集上的最佳Rouge-L分数，其中MINILLM中教师组合的强度$\alpha$不同。$\alpha =0.0$意味着我们只从学生分布中采样，当$\alpha =1.0$时，我们完全从教师分布中采样。我们发现，$\alpha =0.2$通常适用于不同的模型族和大小，较大的模型对$\alpha$的选择更具鲁棒性。
添加预训练损失的影响
在表5中，我们通过将MINLLM与其变体进行比较来研究在算法2.3中添加预训练丢失的影响，其中去除了预训练语料库上的语言建模损失（w/o PT损失）。我们有一个与[$OW{J}^{+}$]类似的观察结果，即添加预训练损失有助于保持规范NLP任务的能力，同时保持指令跟随任务的性能几乎不变。

4 相关工作

大型语言模型
大型语言模型（LLM；$BM{R}^{+}$，Ope，$CN{D}^{+}$，$AD{F}^{+}$，$TDF{H}^{+}$）通过以生成的方式解决各种NLP任务，显示了其优越的性能。最近的工作应用指令调整[$WB{Z}^{+}$，$SW{R}^{+}$，$CH{L}^{+}$]或从人类反馈中学习[$OW{J}^{+}$，$BJ{N}^{+}$]来进一步改善LLM与人类的一致性，并创建通用人工智能助手[Ope，Goo]。此外，还努力构建开源LLM[$TL{I}^{+}$、$ZR{G}^{+}$、$SF{A}^{+}$、$BS{A}^{+}$、Mos]，以促进研究和行业发展。尽管LLM的广泛容量很有吸引力，但通常只有在需要大量计算资源的大参数大小[$KM{H}^{+}$，$WT{B}^{+}$]的情况下才会出现[SGM]。因此，模型压缩对于LLM的实际部署和进一步研究至关重要。
知识蒸馏
知识蒸馏（KD；HVD）旨在在教师模型的指导下训练学生模型，并在深度学习的许多领域被广泛用作模型压缩技术[JBMD，SDCW，$RC{G}^{+}$]。在NLP社区中，许多工作通过训练学生模仿教师的输出分布差异[$SS{T}^{+}$，$ZS{L}^{+}$]、隐藏状态[$JY{S}^{+}$，SCGL]或注意力得分[$WW{D}^{+}$，$WB{H}^{+}$]，将KD应用于文本分类任务。对于文本生成，标准KD方法是通过使用教师在每个时间步长的输出作为监督[SDCW]或对教师生成的直接训练[KR，$TG{Z}^{+}$，$CL{L}^{+}$，$PL{H}^{+}$]来近似最小化学生和教师生成分布之间的正向KLD。在本文中，我们建议最小化反向KLD，当教师分布可用时，反向KLD更适合生成大型语言模型。
文本生成中的分布差异度量
分布差异度量在学习文本生成模型中发挥着重要作用。前向Kullback-Leibler散度（KLD）是标准度量，因为它在作为最大似然估计（MLE）目标推导时很简单[ZZ]。然而，先前的工作表明，最小化前向KLD会导致迫零行为，其中模型试图覆盖目标分布的所有模式，并牺牲主要模式的准确性[Hus]。一些工作采用其他指标来解决这个问题，如反向KLD[$JH{C}^{+}$]、总变化距离[$JK{H}^{+}$]和最优传输[$LL{W}^{+}$]。我们的论文首次解决了LLM知识蒸馏的这一问题。

5 结论

在这项工作中，我们研究了将知识从较大的LLM蒸馏到较小的LLM的问题。我们发现，在语言生成场景中，最小化正向KLD的标准蒸馏 方法是次优的，因为教师的输出分布比学生的输出分布包含更多的模式，并且正向KLD迫使学生分布过度估计教师分布的低概率区域。因此，我们提出了最小化教师和学生分布之间的反向KLD的MINILLM，并开发了一种优化该目标的算法。在指令跟随设置中的大量实验表明，MINILLM模型产生了比标准KD方法更精确的响应，具有更高的整体质量。我们还发现，MINILLM在具有良好多样性的长文本生成中具有更低的曝光偏差、更好的校准和更高的性能。