用SVD分解继续宁特征点三角化
三角化又叫三角测量,本质是用相机的运动估计特征点的空间位置,发生在估计得到帧间运动之后(单目情况)。三角测量是指,通过在两处观察同一个点的夹角,确定该点的距离。由于双目本身就能得到视角不同的两帧图像,所以找到左右双目相机的图像对应的特征点就可以直接进行三角测量。RGB-D相机直接使用物理手段得到深度值,有专门的红外传感器来获得深度。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
在视觉SLAM14讲中,有关深度的求解,如上,就是使用一个等式来分别求解x1和x2的深度值,然后通过深度值来恢复点的空间坐标。
SVD方法:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这里首先将平面坐标和世界坐标进行表示,然后利用平行的性质,来进行叉积为0的表达。
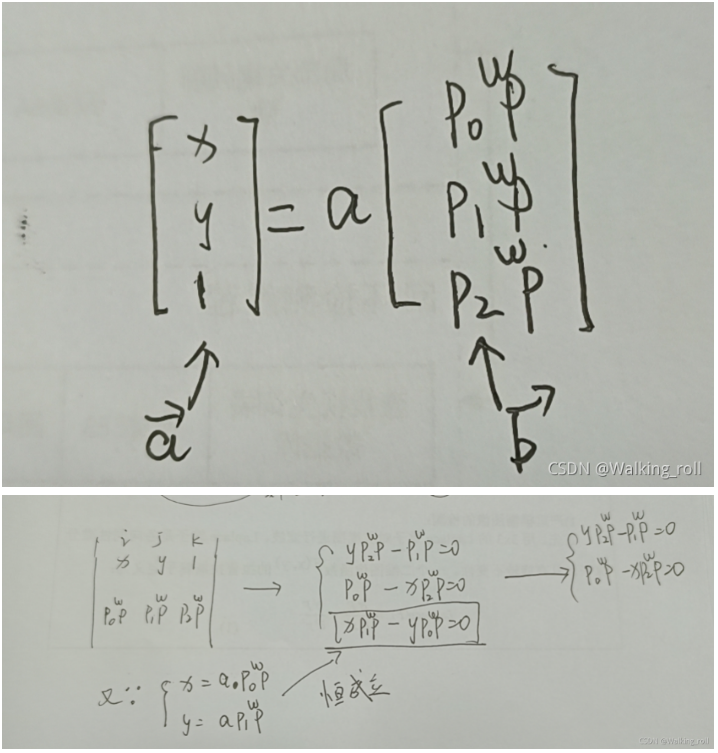
编辑切换为居中
添加图片注释,不超过 140 字(可选)
以上为叉积的表达,得到了两个等式。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
左目2个方程,右目两个方程,通过四个方程来求解世界坐标,即达到了三角化的目的。
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
// 通过奇异值分解求解一个Ax = 0得到
Matrix4d design_matrix = Matrix4d::Zero();
design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
Vector4d triangulated_point;
triangulated_point =
design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
// 齐次向量归一化
point_3d(0) = triangulated_point(0) / triangulated_point(3);
point_3d(1) = triangulated_point(1) / triangulated_point(3);
point_3d(2) = triangulated_point(2) / triangulated_point(3);
}
vins里面的代码如上,上面design_matrix相关的就是通过叉积进行的等式表达,然后求解世界坐标即可成功三角化。最后再进行一步齐次向量归一化即可。