1.什么是Haar特征

Haar特征是一种反映人脸灰度差异的矩形特征，因其与Haar小波类似而得名。

2.什么是Haar小波

Haar小波：

定义

其波形图为

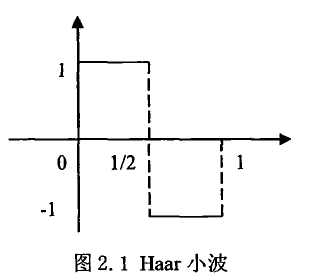
由图2.1可以看出，Haar小波可以看作二值

分类问题，如同Haar矩阵特征非黑即白，故Haar矩阵特征又称为类Haar特征。

3.Haar特征

Haar特征也称为矩形特征，它是由两个或多个形状大小相同的矩阵组合而成。常用的Haar特征如下图所示：

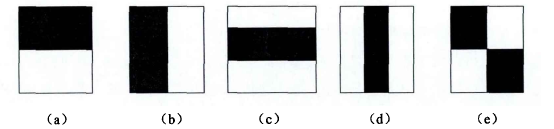
4.Haar特征值计算中中引入积

分图

Haar特征的特征值可以表示为：

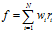
表示所选Haar特征中黑、白矩形的总个数，表示每种类型的矩形对应的权值，表示矩形区域内像素值的和。