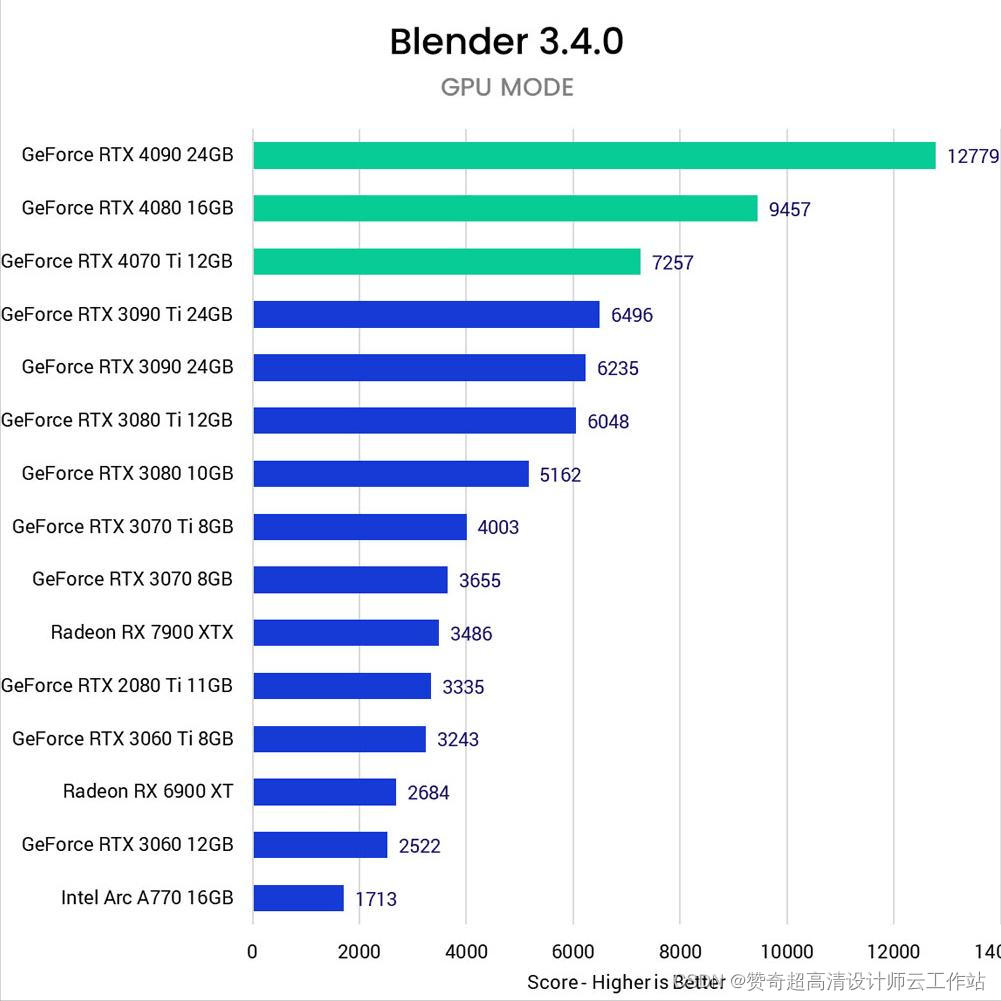
黏菌算法是2020年提出的一种智能优化算反,主要模拟的是自然界中多头绒泡菌在不同食物浓度下的觅食行为以及状态变化。黏菌主要分泌酶来消化食物,黏菌的前端延伸成扇形,后端由相互连接的静脉网络包围。环境中不同浓度的食物影响着黏菌静脉网络中细胞质的流动,从而形成黏菌觅食的不同状态。
1.算法原理
当黏菌接近食物时,黏菌算法的数学模型如下式表示:
其中,t为当前迭代次数,Xb(t)为第t次迭代时黏菌个体最优的位置,Xm(t)和Xn(t)为随机选择两个黏菌个体的位置,vb作为控制参数范围是[-a,a],vc是从1线性下降到0的参数,r是[0,1]之间的随机值。W为黏菌质量,代表适应度权重。控制变量p和参数vb的数学模型公式如下:
a的计算公式如式:

其中,i∈1,2,3…,n,S(i)是第 i 个黏菌适应度值,DF为所有迭代中最佳适应度值。适应度权重 W 如式所示:
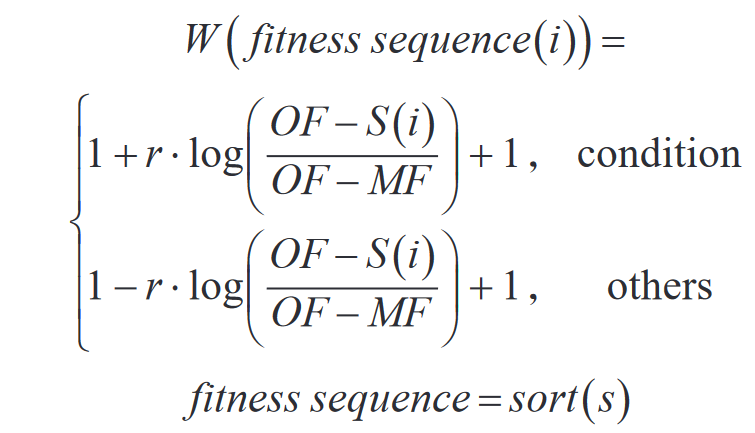
其中,condition 表示适应度值排在前一半的黏菌个体。fitness sequence 为黏菌的适应度值序列,当求解最小值问题时,其使用升序排列方法。其中,目前迭代次数中最优适应度值用 OF 表示,最差适应度值用 MF 表示。当黏菌包裹食物时,黏菌算法的数学模型如式所示:

当黏菌抓取食物时,黏菌的静脉组织和生物振荡器产生变化。静脉接触的食物浓度越高,生物振
荡器产生的波越强,依靠这种变化,黏菌会抓取更高浓度的食物。黏菌静脉宽度的变化采用 W、vb 和vc 来实现。W 模拟了不同食物浓度下黏菌在附近的振荡频率。vb 在[-a,a]之间随机变化,随着迭代次数的增加,逐渐趋近于零。vc 的值在[-1,1]之间振荡,最终趋于 0。当黏菌选择食物时,vb 和 vc 之间的相互协同性发挥着重要的作用。
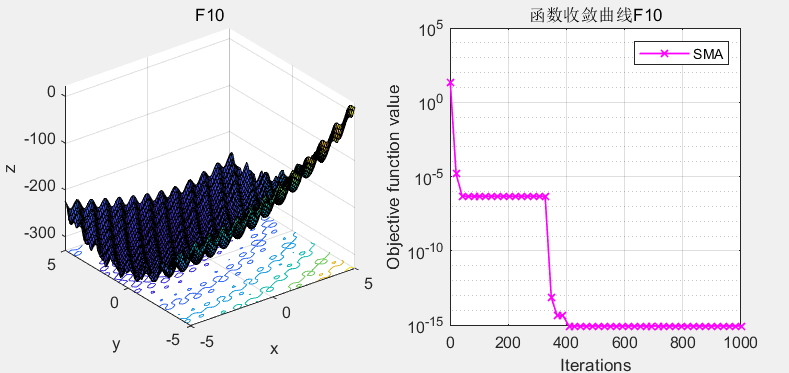
2.结果展示
以为CEC2005函数集为例,进行结果展示



3.MATLAB核心代码
% 黏菌优化算法(SMA)
% max _ iter:最大迭代次数,N:种群大小,收敛曲线:收敛曲线,
function [Destination_fitness,bestPositions,Convergence_curve]=SMA(N,Max_iter,lb,ub,dim,fobj)
%% 初始化位置
bestPositions=zeros(1,dim);
Destination_fitness=inf;%将此更改为 -inf 以解决最大化问题
AllFitness = inf*ones(N,1);%记录所有粘菌的适应度
weight = ones(N,dim);%每个粘菌的适应度权重
%% 初始化随机解集
X=initialization(N,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
it=1; %迭代次数
lb=ones(1,dim).*lb; % 变量下限
ub=ones(1,dim).*ub; % 变量上限
z=0.03; % 参数
%% 主循环
while it <= Max_iter
%=====适应度排序======
for i=1:N
% 检查解决方案是否超出搜索空间并将其带回
Flag4ub=X(i,:)>ub;
Flag4lb=X(i,:)<lb;
X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
AllFitness(i) = fobj(X(i,:));
end
[SmellOrder,SmellIndex] = sort(AllFitness);
worstFitness = SmellOrder(N);
bestFitness = SmellOrder(1);
S=bestFitness-worstFitness+eps; %加上 eps 以避免分母为零
%====计算每个粘菌的适应度权重=====
for i=1:N
for j=1:dim
if i<=(N/2)
weight(SmellIndex(i),j) = 1+rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
else
weight(SmellIndex(i),j) = 1-rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
end
end
end
%====更新最佳适应度值和最佳位置=====
if bestFitness < Destination_fitness
bestPositions=X(SmellIndex(1),:);
Destination_fitness = bestFitness;
end
a = atanh(-(it/Max_iter)+1);
b = 1-it/Max_iter;
%====更新搜索代理的位置=====
for i=1:N
if rand<z
X(i,:) = (ub-lb)*rand+lb;
else
p =tanh(abs(AllFitness(i)-Destination_fitness));
vb = unifrnd(-a,a,1,dim);
vc = unifrnd(-b,b,1,dim);
for j=1:dim
r = rand();
A = randi([1,N]); % 从总体中随机选择两个位置
B = randi([1,N]);
if r<p
X(i,j) = bestPositions(j)+ vb(j)*(weight(i,j)*X(A,j)-X(B,j));
else
X(i,j) = vc(j)*X(i,j);
end
end
end
end
Convergence_curve(it)=Destination_fitness;
display(['At iteration ', num2str(it), ' the best solution fitness is ', num2str(Destination_fitness)]);
it=it+1;
end
end完整代码获取方式:下方小卡片回复关键字:TGDM1209
参考文献:
[1] Li S, Chen H, Wang M, et al. Slime mould algorithm: A newmethod for stochastic optimization[J]. Future Generation Computer Systems. 2020, 111(1): 300-323.
[2]龚然,施文娟,朱振源.基于混沌映射和莱维飞行的黏菌优化算法[J].计算机与数字工程,2023,51(02):361-367.