思维导图:
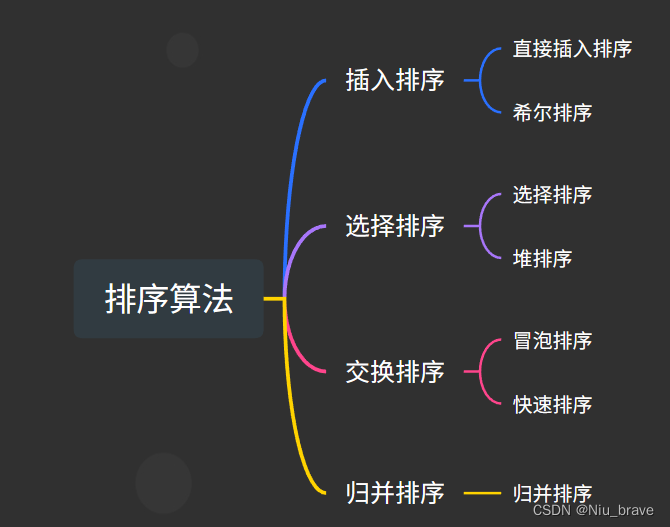
一,插入排序
插入排序,一种简单排序中的王者。这种排序算法的过程可以想象成是打牌时摸牌按照顺序插入扑克牌的过程。想想你是如何打牌的?在你拿下一个牌插入时你是不是将手里已经有的牌变得有序了才抽下下一个牌来进行插入呢?想到这一点我们就可以来写这个代码了。
代码:
void InsertSort(int* a, int n)
{
for (int i = 1;i < n;i++)
{
int end = i-1;
int tmp = a[i];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}代码分析:
比如我要排序以下数组:
我的代码是如何走的呢?
首先:i = 1,end = 0
这时因为tmp>a[end],所以跳出while循环在a[end+1]的位置上放入tmp这个值。
后面的各个操作也是如此,当a[end] = 7时便要开始发生交换了。
便是这时:
当到了在这种情况时,5,6,7都是需要往后移一步将0后面的位置让给4然后a[end] = 0。就
是这样:
之后再执行跳出while循环的操作。用这个逻辑使用后数组内的元素就会变得有序。
插入排序的时间复杂度
先说结论:插入排序的时间复杂度是在:O(n)与O(n^2)之间,当数组是正序的时侯使用这个排序的时间复杂度便是O(n),当数据是逆序的时候时间复杂度便是O(n^2)。这两种情况便是最好与最差的情况,其它的情况的复杂度则在这两种情况的复杂度之间。
二,希尔排序
希尔排序是插入排序的改进版本。希尔排序的总体思路:
1.预排序。
2.插入排序。
话不多说,先上个希尔排序的代码。
代码:单趟
void Shellsort(int* a, int n)
{
int gap = 3;//
for (int i = 0;i < n - gap;i+=gap)
{
int end = i;
int tmp = a[i+gap];
while (end>=0)
{
if (tmp < a[end])
{
a[end+gap] = a[end ];
a[end] = tmp;
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}这是希尔排序的一趟排序,比如我要排序这个数组:
这个算法便将其根据gap的大小分成这样三组:
这个单趟排序便是将红色线连成的这一组进行预排序。排序后:
可以看到这一组数据果然有序了:8,7,1---》1,7,8
多趟:
单趟排序既然已经实现了,那我们就要实现多趟了。这个操作的实现很简单,加个循环便是。
代码:
void Shellsort(int* a, int n)
{
int gap = 3;//
for (int j = 0;j < gap;j++) //加循环
{
for (int i = j;i < n - gap;i += gap)//i随着j变化来控制排序不同的组
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
a[end] = tmp;
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}两层循环写法:
void Shellsort1(int* a, int n)
{
int gap = 3;//
for (int i = 0;i < n - gap;i++)
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
a[end] = tmp;
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}排序效果:
从图中可以看出这个数组变得相对有序了但还不是有序的。
在这个时候,我们便拿gap开刀,先将gap变成2看看:
排序效果:
将gap变成1:
对比:
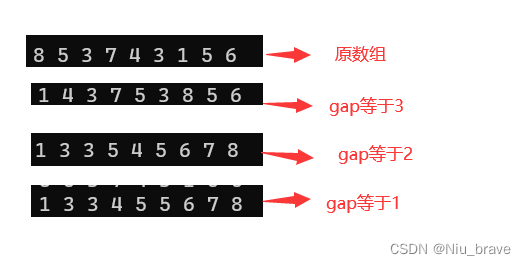
可以看到当gap越来越来越小时 数组就变得越来越有序。但是gap变小,程序的执行速度就会变慢,所以为了速度与目的的双向奔赴我们可以对gap的大小进行控制让gap从大到小的变化直到gap变成1变成插入排序。
代码:
void Shellsort(int* a, int n)
{
int gap = n;//最大的gap
while (gap > 1) {
gap = gap / 3 + 1;//最小为gap为1
for (int i = 0;i < n - gap;i++)
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
a[end] = tmp;
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}通过以上的操作我们便实现了一个希尔排序的代码,希尔排序是对插入排序的优化。它的时间复杂度是难以计算的,大概是O(n^1.3)。