我们改进了第一次迭代：第二次迭代如下：因为三个弱分类器都是犯了3次错误，我们故意选了y>6.5,标签=1，else，标签=-1；第一个弱分类器已经选了，再选一次没意义，不会有任何进展，和第一次迭代一模一样。先看代码：

   float[] 第er个弱分类器jieguo = new float[] { -1, -1, -1, -1, 1,-1, 1, 1, 1, -1 };
            float[] 最初的标签样本       = new float[] {  1,  1, -1, -1, 1, -1, 1, 1, -1, -1 };
            //以上两个数组相乘，ok为1，ng为-1，
            //1,2,9分错值为-1，数组序号0，1，8
            //第一个弱分类器的错误率0.16*3=0.48
            //第二个弱分类器的错误率0.07*3=0.21，0.21<0.48,所以选第二个弱分类器作为第二次迭代,并且更新dataP。
            for (int j = 0; j < example.Count; j++)
            {
                if (第er个弱分类器jieguo[j] * 最初的标签样本[j] == -1.0f)
                {
                    //分错的变大
                    dataP[j] = dataP[j] / (2 * (3 * 0.07f));
                }
                if (第er个弱分类器jieguo[j] * 最初的标签样本[j] == 1.0f)
                { //分对的变小
                    dataP[j] = dataP[j] / (2 * (1 - 3 * 0.07f));
                }               
            }
            //计算a2=1/2ln((1-e)/e)
            double a2 = 0.5 * Math.Log(0.79 / 0.21);
          //  float[] jieguo2 = new float[] { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
            for (int i = 0; i < 10; i++)
            {
                if (a2 * 第er个弱分类器jieguo[i]+ a1 * 第一个弱分类器jieguo[i] > 0)
                    jieguo[i] = 1;
                if (a2 * 第er个弱分类器jieguo[i]+ a1 * 第一个弱分类器jieguo[i] < 0)
                    jieguo[i] = -1;
                if (a2 * 第er个弱分类器jieguo[i]+ a1 * 第一个弱分类器jieguo[i] == 0)
                    jieguo[i] = 0;
            }

看第一次迭代后的权重变化：

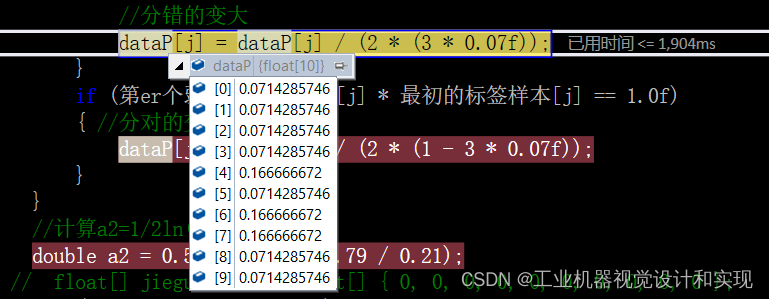
第二次迭代完成后，对比如下：

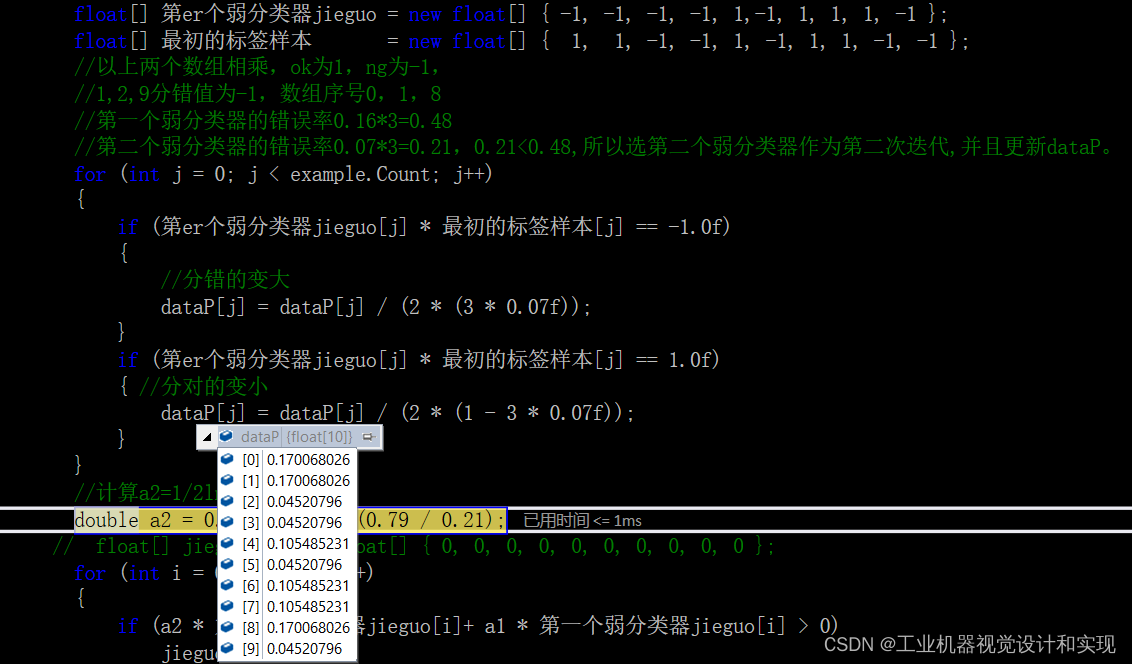
明显，1，2，9项分错了。我们继续计算a2：

 继续计算第二个强分类器（两个弱分类器组合，结果仍不能达标，继续级联第三个，如果还不行，继续第四个，犯错误为4的可选）：

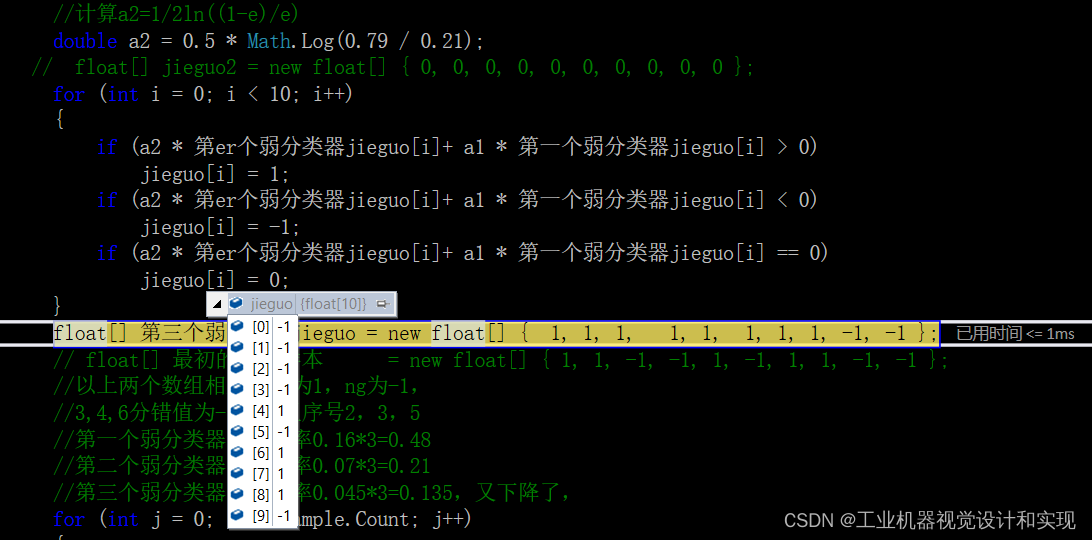
 ok，这一节也算完成了。