14-2利用遗传算法求解BP神经网络初始化权值和阈值的最优问题（附matlab程序）

news2024/10/7 6:45:51

1.简述

核心问题：

BP网络是前向网络的核心部分，是神经网络中的最精华、最完美的部分，由于其简单的结构，可调整的参数多，训练算法也多，而且可操作性好，BP神经网络获得了非常广泛的应用，但是也存在着一些缺陷，例如学习收敛速度太慢、不能保证收敛到全局最小点、网络结构不易确定。另外，网络结构、初始连接权值和阈值的选择对网络训练的影响很大，但是又无法准确获得，针对这些特点可以采用遗传算法对神经网络进行优化。

遗传算法优化BP神经网络主要分为：BP神经网络结构确定、遗传算法优化权值和阈值、BP神经网络训练及预测。其中，BP神经网络的拓扑结构是根据样本的输入/输出参数个数确定的，这样就可以确定遗传算法优化参数的个数，从而确定种群个体的编码长度。因为遗传算法优化参数是BP神经网络的初始权值和阈值，只要网络结构已知，权值和阈值的个数就已知了。神经网络的权值和阈值一般是通过随机初始化为[-0.5，0.5]区间的随机数，网络的训练结果是一样的，引入遗传算法就是为了优化出最佳的初始权值和阈值。

神经网络算法实现：
网络创建：BP神经网络的确定有以下两条重要的指导原则。
1.对于一般的模式识别问题，三层网络可以很好地解决问题。
2.在三层网络中，隐含层神经网络个数n2和输入层神经元个数n1之间有近似关系：

遗传算法实现：
遗传算法优化BP神经网络是用遗传算法来优化BP神经网络的初始权重值和阈值，使优化后的BP神经网络能够更好地进行样本预测。遗传算法优化BP神经网络的要素包括种群初始化、适应度函数，选择算子、交叉算子和变异算子。
（1）种群初始化
个体编码使用二进制编码,每个个体均为一个二进制串，由输人层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值、输出层阈值四部分组成,每个权值和阈值使用M位的二进制编码,将所有权值和阈值的编码连接起来即为一个个体的编码。

（2）适应度函数
本案例是为了使BP网络在预测时，预测值与期望值的残差尽可能小，所以选择预测样本的预测值与期望值的误差矩阵的范数作为目标函数的输出。适应度函数采用排序的适应度分配函数：FitnV = ranking(obj)，其中obj为目标函数的输出。

（3）选择算子
选择算子采用随机遍历抽样(sus)。

（4）交叉算子
交叉算子采用最简单的单点交叉算子。

（5）变异算子
变异以一定概率产生变异基因数，用随机方法选出发生变异的基因。如果所选的基因的编码为1，则变为0；反之，则变为1。

遗传算法主函数
遗传算法主函数流程为：
（1）随机初始化种群。
（2）计算种群适应度值，从中找出最优个体。
（3）选择操作。
（4）交叉操作。
（5）变异操作。
（6）判断进化是否结束；若否，则返回步骤（2）。

比较使用遗传算法前后的差别
经过遗传算法优化之后得到最佳的初始权值与阈值矩阵，可以将该初始权值和阈值回代入网络画出训练误差曲线、预测值、预测误差、训练误差等。使用以下代码可以比较优化前后的差别，其中bestX参数为前面优化得到的最优初始权重值和阈值矩阵。

2.代码

%% I. 清除环境变量
clear all
clc

%% II. 声明全局变量
global p % 训练集输入数据
global t % 训练集输出数据
global R % 输入神经元个数
global S2 % 输出神经元个数
global S1 % 隐层神经元个数
global S % 编码长度其实就是连接权值个数和阈值个数的总和
S1 = 10;

%% III. 导入数据
%%
% 1. 训练数据 6-10-4 6*10+10*4+10+4
p = [0.01 0.01 0.00 0.90 0.05 0.00;
0.00 0.00 0.00 0.40 0.50 0.00;
0.80 0.00 0.10 0.00 0.00 0.00;
0.00 0.20 0.10 0.00 0.00 0.10]';
t = [1.00 0.00 0.00 0.00;
0.00 1.00 0.00 0.00;
0.00 0.00 1.00 0.00;
0.00 0.00 0.00 1.00]';
%%
% 2. 测试数据
P_test = [0.05 0 0.9 0.12 0.02 0.02;
0 0 0.9 0.05 0.05 0.05;
0.01 0.02 0.45 0.22 0.04 0.06;
0 0 0.4 0.5 0.1 0;
0 0.1 0 0 0 0]';

%% IV. BP神经网络
%%
% 1. 网络创建
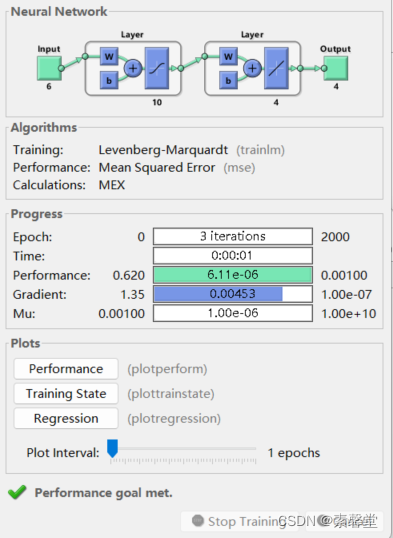
net = newff(minmax(p),[S1,4],{'tansig','purelin'},'trainlm');

%%
% 2. 设置训练参数
net.trainParam.show = 10;
net.trainParam.epochs = 2000;
net.trainParam.goal = 1.0e-3;
net.trainParam.lr = 0.1;

%%
% 3. 网络训练
[net,tr] = train(net,p,t);

%%
% 4. 仿真测试
s_bp = sim(net,P_test) % BP神经网络的仿真结果

%% V. GA-BP神经网络
R = size(p,1);
S2 = size(t,1);
S = R*S1 + S1*S2 + S1 + S2; %计算过了刚才 114
aa = ones(S,1)*[-1,1];

%% VI. 遗传算法优化
%%
% 1. 初始化种群
popu = 50; % 种群规模
initPpp = initializega(popu,aa,'gabpEval',[],[1e-6 1]); % 初始化种群 gabpEval 看一下这个函数，还调用了gadecod

%%
% 2. 迭代优化
gen = 100; % 遗传代数
% 调用GAOT工具箱，其中目标函数定义为gabpEval endpop 前114列吻合S，115列代表适应度函数值
[x,endPop,bPop,trace] = ga(aa,'gabpEval',[],initPpp,[1e-6 1 1],'maxGenTerm',gen,...
'normGeomSelect',[0.09],['arithXover'],[2],'nonUnifMutation',[2 gen 3]);
%%
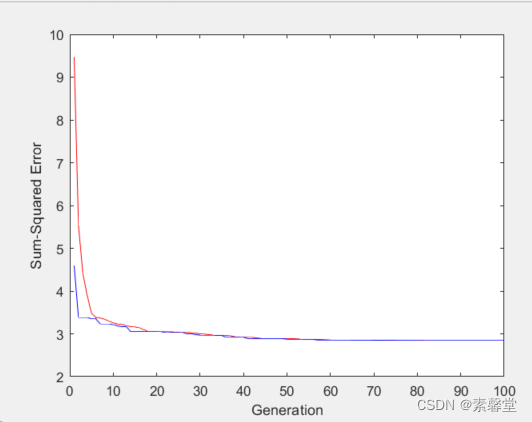
% 3. 绘均方误差变化曲线
figure(1)
plot(trace(:,1),1./trace(:,3),'r-');
hold on
plot(trace(:,1),1./trace(:,2),'b-');
xlabel('Generation');
ylabel('Sum-Squared Error');

%%
% 4. 绘制适应度函数变化
figure(2)
plot(trace(:,1),trace(:,3),'r-');
hold on
plot(trace(:,1),trace(:,2),'b-');
xlabel('Generation');
ylabel('Fittness');

%% VII. 解码最优解并赋值
%%
% 1. 解码最优解
[W1,B1,W2,B2,val] = gadecod(x);

%%
% 2. 赋值给神经网络
net.IW{1,1} = W1;
net.LW{2,1} = W2;
net.b{1} = B1;
net.b{2} = B2;

%% VIII. 利用新的权值和阈值进行训练
net = train(net,p,t);

%% IX. 仿真测试
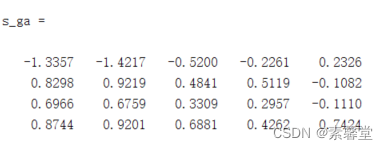
s_ga = sim(net,P_test) %遗传优化后的仿真结果

3.运行结果