目录
1.什么是浮点数
2.举个例子
2.1.十进制转二进制
2.2.规范尾数位
2.3.计算指数位
2.4.拼接结果
3.精度丢失
4.JAVA中的浮点数思考
1.什么是浮点数
在计算机系统的发展过程中,曾经提出过多种方法表示实数,但是到为止使用最广泛的是浮点表示法。浮点表示法,即用浮点数来表示实数,所谓浮点数,意思是小数点的位置不是固定的,是可以浮动的。浮点数采用IEEE 754这个标准作为统一的标准。该标准中严格定义个浮点数的表示格式、转化过程。
下面简单介绍一下IEEE 754标准。
IEEE 754的核心就是用科学计数法来表示实数,然后将表示结果转为二进制的方式,方便计算机存储。
例如250,在科学计数法中表示为2.5x10^2。
可以这样来描述以上的科学计数法的结果:
+2 2.5
+是表示正负的符号位,2是指数位,2.5是开头的数。
IEEE 754将上面的这种表示思路引入计算机中适配计算机中二进制的表示法,规定浮点数的表示格式为:
位符号位 位指数位 位尾数位
本文以单精度浮点数为例(双精度只是位数的长度不一样而已),单精度浮点数的格式如下:
1位符号位 8位指数位 23位尾数位
2.举个例子
以下举一个例子,0.75用单精度浮点数表示的过程:
2.1.十进制转二进制
0.75x2=1.5,整数位为1,小数位为0.5
0.5x2=1,整数位为1,小数位为0
0.75转成二进制小数结果为0.11
2.2.规范尾数位
规范尾数位的意思是,将小数点右移,直到出现整数位不为0的时候为止,0.11规范后的结果是:
1.1
小数点右移了一位
由于有23位的空间大小,于是用0填充上:
1.100000000000000000000000
由于开头整数位一定是1,所以规范里采取了简略的表示,将整数部分略去,最后规范结果为:
100000000000000000000000
2.3.计算指数位
指数位用来表示小数点移动了多少位,也就是指数位的取值范围就决定了整个数据能表示的范围。指数位用给了8位的长度,也就是说按理说指数位最大是255,但是第一位被留作了符号位,所以能表示值的只有后七位,所以整个符号位的表示范围是-127到+127。
之所以要考虑到负的指数值,是因为小数点即要考虑到左移的情况,也要考虑到右移的情况。
比如,110.001,在规范尾数位的时候就要左移,那么指数位就应该是复数。
比如,0.11,在规范尾数位的时候就要右移,那么指数位就应该是正数。
说明白这些后,我们继续向下计算。上面一步我们将小数点右移了一位,按理说指数位的值应该是1,但规范里面这里比较特别,默认指数位的初始值不是0而是127,如果是左移1位的话就127+1,右移一位的话就是127-1。
上面我们将小数右移了1位,于是指数位是:
01111110
2.4.拼接结果
最终结果为:
0 01111110 10000000000000000000000
3.精度丢失
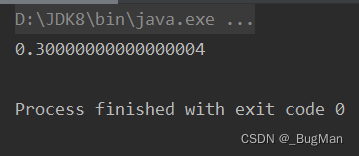
来看一个JAVA中浮点数精度丢失的问题:
double a=0.1;
double b=0.2;
System.out.println(a+b);结果会是:
看完前面浮点数的转化过程,应该就能想明白了,0.1和0.2在转二进制的时候是没办法转干净。
0.1转二进制:
0.0001100110011001100110011001100110011001100110011...
0.2转二进制:
0.00110011001100110011001100110011001100110011001101...
所以将他们转浮点数后再进行运算,运算的结果转十进制输出,输出的结果一定不会是0.3。这就是一切浮点数运算中精度丢失的根本原因。
4.JAVA中的浮点数思考
为什么叫浮点数:
现在我们知道为什么JAVA中的小数叫浮点数了吧,因为就是用浮点数规范进行表示的小数。
为什么float的长度是32位:
上面我们提到过单精度浮点数的表示格式是:
1位符号位 8位指数位 23位尾数位
这里我们就能知道为什么Java的float长度为32位了。
为什么float的取值范围是正负3.4乘以10的38次方:
上面我们也提到了单精度的浮点数的指数位的取值范围是-127到+127,所以可以推导出来单精度浮点数能表示的范围是正负3.4乘以10的38次方,正好和JAVA中float的表示范围吻合。