今天我们继续,接着昨天的进度。
先回顾一下上一小节,我学到了构建起一个模型函数和一个损失函数,然后我们使用人眼观察损失,并手动调整模型参数。然而看起来,我们虽然看到了损失,但我们调整参数的方案跟损失并没有太大的关系,而是随机的进行了调整,那么有没有什么方法能够衡量我们的参数该往什么方向去调整呢?是该调大还是调小呢?这里就涉及到一个梯度的概念了。
梯度(gradient)
百科给梯度的定义是这样的,反正我是没太看得懂。大学数学学得知识也忘得差不多了。
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
简单来说对于函数的某个特定点,它的梯度就表示从该点出发,函数值增长最为迅猛的方向(direction of greatest increase of a function)。而我们这里所要求的就是loss关于参数w和偏置b的梯度,然后沿着这个梯度去修正我们的w和b。
这里举个例子,想像当年上大学的时候,女生宿舍楼就在你的窗户后面,于是你买了一个望远镜,想窥探一下女生宿舍的生活细节。夜黑风高,对面的女生宿舍楼都亮起了灯光。这个时候你掏出了新买的望远镜,但是你发现看不清楚,可以说非常模糊,这时候你摸索着望远镜,上面有两个旋钮,一个是可以调整清晰度,一个是调整放大倍率(这里可以看做是w和b),这时候你发现向左拧按钮w就更模糊了,向右拧w就清楚一点,所以在当前这个点,向右就是你要的梯度。你发现向右可以变清楚,于是你喜出望外,大力往右一拧,貌似有那么一瞬间清晰,但是又变得模糊起来,这个时候向左就是你要的梯度。
把这个事情转换成数学公式,就是计算loss对于每一个参数的导数,然后在一个具体点位获得的矢量就是梯度结果。
即
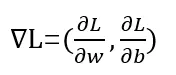
image.png
根据求导的链式法则,有如下结果
d loss_fn / d w = (d loss_fn / d t_p) * (d t_p / d w)
对参数b同样适用
d loss_fn / d b = (d loss_fn / d t_p) * (d t_p / d b)

image.png
这个时候,我们写成代码
def dloss_fn(t_p, t_c): #loss对t_p求导
dsq_diffs = 2 * (t_p - t_c) / t_p.size(0) # <1>
return dsq_diffs
def dmodel_dw(t_u, w, b): #t_p对w求导
return t_u
def dmodel_db(t_u, w, b): #t_p对b求导
return 1.0
梯度函数
def grad_fn(t_u, t_c, t_p, w, b):
dloss_dtp = dloss_fn(t_p, t_c)
dloss_dw = dloss_dtp * dmodel_dw(t_u, w, b)
dloss_db = dloss_dtp * dmodel_db(t_u, w, b)
return torch.stack([dloss_dw.sum(), dloss_db.sum()])
对于stack方法的官方解释:沿着一个新维度对输入张量序列进行连接。 序列中所有的张量都应该为相同形状。
浅显说法:把多个2维的张量凑成一个3维的张量;多个3维的凑成一个4维的张量…以此类推,也就是在增加新的维度进行堆叠。
说一句,我理解这个计算梯度的过程就叫反向传播。
学习率
通过求梯度,我们能知道该往哪个方向走是loss下降最快的,然而,到底该迈多大的步子呢?想到这个问题,我不禁又掏出了望远镜。当我们发现大力拧望远镜的时候,很容易就拧过去了,一下子就从一种模糊状态变成了另一种模糊状态,中间有一个清晰的妹子图像一闪而过。于是我决定控制好抖动的双手,每次只拧一点点,这样我才能够在看清妹子的时候停下来。
所以,这里面涉及到的一个概念就是学习率(learning rate)。前面我们通过梯度确定了参数的调整方向,然后我们用学习率来调整步子的大小,其实就是在梯度上面乘以一个系数,比如说w = w - learing_rate * grad作为我们下次尝试的参数。
可以想到的是,如果学习率定的太大,可能很难收敛,就像你的望远镜一直在两种不同的模糊状态中变来变去,而你的学习率定的太小,也会很难收敛,比如你每次只转动0.0001毫米,估计对面的女生都毕业了你也没转到清楚的地方。因此这个学习率也是一个玄学,有时候在搞模型的时候会让你有意想不到的情况发生。当然,很多时候也有一些参考值,比如设定为1e-5。
如何优化
说到这里,我们训练的前期准备都差不多完成了,接下来开启炼丹过程。
这里有一个概念就是epoch,话说epoch原意是时代,这里其实就是循环训练了几次的意思,一个epoch就是一次训练修正参数的过程,这原创人真的能整活,一个循环跑下来,一个时代就过去了。不过想想也是,深度模型实在是太费资源,如果你资源不充足,跑的是真慢,大厂有句老话,一杯茶,一包烟,一个模型跑一天。
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
for epoch in range(1, n_epochs + 1):
w, b = params
t_p = model(t_u, w, b) # 正向传播,数据输入模型获得预测结果
loss = loss_fn(t_p, t_c) #计算预测结果和真实值的损失
grad = grad_fn(t_u, t_c, t_p, w, b) # 反向传播,求损失关于参数的梯度
params = params - learning_rate * grad #参数调整
print('Epoch %d, Loss %f' % (epoch, float(loss)))
return params
# 定义好了训练迭代的方案,开始跑训练
training_loop(
n_epochs = 100, #100个时代
learning_rate = 1e-2, #学习率初始化
params = torch.tensor([1.0, 0.0]), #参数初始化
t_u = t_u,
t_c = t_c)
搞了这么多,结果还是出问题了,你猜怎么着,看起来这效果一点也不好啊,这每轮训练不光没有降低损失,反而让损失越来越大,到了第11代直接溢出了,好嘛。

image.png
这里你想到什么问题,就是我们前面说的学习率过大了,那我们就把学习率调小一点,其他的不变,把学习率改到1e-5,同时把grad和params也输出看一下。
看前5次迭代,明显效果好多了,至少loss是在下降的。
Epoch 1, Loss 1763.884766
params:tensor([ 9.5483e-01, -8.2600e-04])
grad:tensor([4517.2964, 82.6000])
Epoch 2, Loss 1565.761353
params:tensor([ 0.9123, -0.0016])
grad:tensor([4251.5220, 77.9184])
Epoch 3, Loss 1390.265503
params:tensor([ 0.8723, -0.0023])
grad:tensor([4001.3838, 73.5123])
Epoch 4, Loss 1234.812378
params:tensor([ 0.8346, -0.0030])
grad:tensor([3765.9622, 69.3654])
Epoch 5, Loss 1097.112793
params:tensor([ 0.7992, -0.0037])
grad:tensor([3544.3916, 65.4625])
看最后一代,loss降到了29,其实到第64代的时候,loss就已经在29-30之间徘徊了,看起来这就是当前的一个极限水平了。
Epoch 100, Loss 29.114819
params:tensor([ 0.2340, -0.0165])
grad:tensor([11.1109, 3.2240])
那么还有什么地方是可以优化的呢?我们观察一下结果,在params上,参数w和参数b基本上有10倍的差距,而我们使用同一个学习率那么可能导致一些问题,如果说这个学习率对较大的那个参数比较合适,那么比较小的那个肯定是属于优化过慢,而如果学习率比较适合较小的那个参数,那么较大的那个就属于步子太大可能不稳定。这个时候我们自然想到的是给每一个参数设定一个不同的学习率,但是这个成本很高,至少目前看起来是很高,因为我们在深度模型里可能会有几十亿的参数,那就需要有几十亿的学习率。
反过来,这里有一个比较简单的方案,既然调整学习率不方便,那么我们就想别的办法。比如说做输入数据的归一化。因为参数和数据合并起来构成一项,如果我们把所有维度的输入数据都限定到一个固定的区间中,那么学习率的影响也应该是类似的。
这里我们做个简单的尝试,把t_u都缩小10倍,使用params来承接输出结果
t_un = 0.1 * t_u
params=training_loop(
n_epochs = 100, #100个时代
learning_rate = 1e-5, #学习率初始化
params = torch.tensor([1.0, 0.0]), #参数初始化
t_u = t_un,
t_c = t_c)
结果呢,到了100代loss才降到74,而且观察前100,loss是稳定下降的,这说明我们的学习率太小了,这个时候可以增大epoch,或者增大学习率。
Epoch 100, Loss 74.637016
params:tensor([1.0753, 0.0102])
grad:tensor([-73.1205, -9.8467])
当把epoch改到3000的时候,loss下降到了30,还不如之前效果好,看来还得加大epoch
Epoch 3000, Loss 30.896944
params:tensor([2.0809, 0.0991])
grad:tensor([-13.0219, 0.7548])
或者我们把学习率改到1e-2试一下,epoch为100,这个时候可以看到loss已经降到了22,说明我们的优化起到了效果。
Epoch 100, Loss 22.148710
params:tensor([ 2.7553, -2.5162])
grad:tensor([-0.4446, 2.5165])
这个时候让我们双管齐下,学习率使用1e-2,迭代次数3000次,可以看到这时候loss虽然还没有到0,但是跟之前比起已经非常小了,只有2.9,当然我们的数据本来就有一些误差,所以肯定到不了0。
Epoch 3000, Loss 2.928648
params:tensor([ 5.3489, -17.1980])
grad:tensor([-0.0032, 0.0182])
最后,让我们把我们预测完的模型图像绘制出来,就是一个直线
这里面用到一个新的参数传入方式“*”,就像下面代码里写的,t_p = model(t_un, *params),这里是解包方法,意味着接受到的参数params中的元素作为单独的参数传入,等同于model(t_un, params[0],params[1])
%matplotlib inline
from matplotlib import pyplot as plt
t_p = model(t_un, *params)
fig = plt.figure(dpi=600)
plt.xlabel("Temperature (°Fahrenheit)")
plt.ylabel("Temperature (°Celsius)")
plt.plot(t_u.numpy(), t_p.detach().numpy())
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.savefig("temp_unknown_plot.png", format="png")
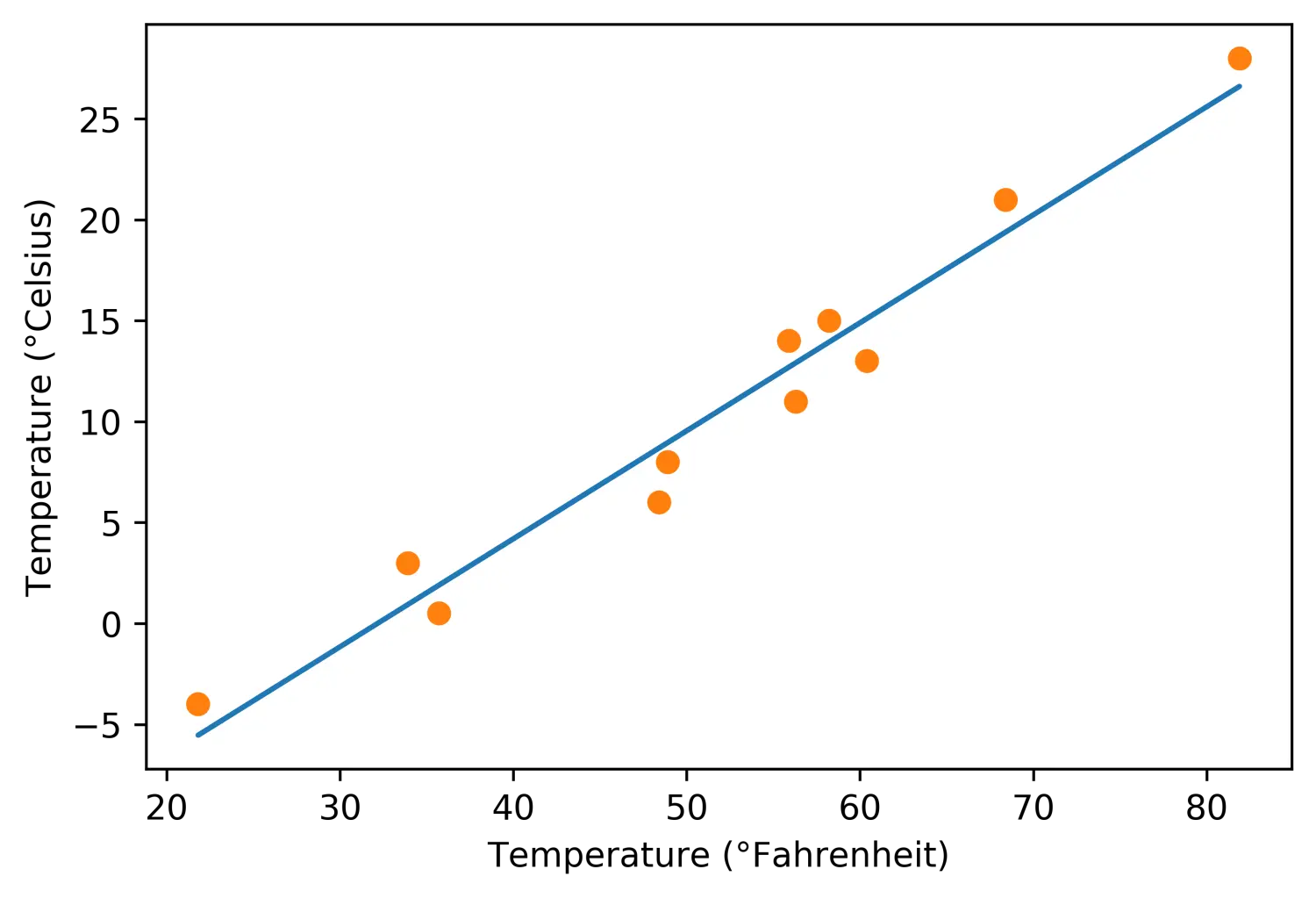
image.png
总结一下今天这一小节,关于构建模型这一部分,我们了解了梯度这个概念,知道了怎么计算梯度以及梯度下降方法用于更新参数,然后了解了学习率以及学习率对更新参数的影响。最后学了一点点优化方法,比如像归一化数据,如何修改学习率,增大epoch等等,每天进步一点点。