一.梯度下降(gradient descent)
1.预测函数
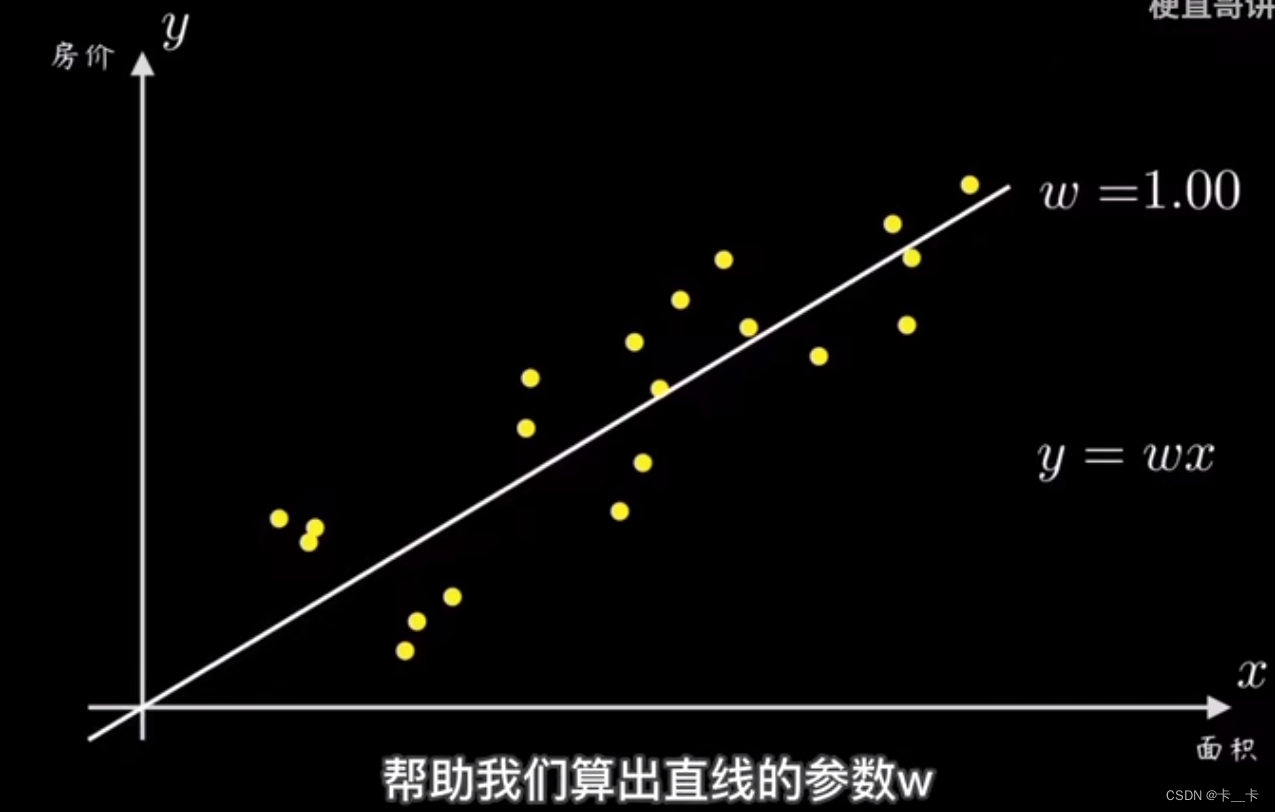
这里有一组样本点,横纵坐标分别代表一组有因果关系的变量

我们的任务是设计一个算法,让机器能够拟合这些数据,帮助我们算出参数w
我们可以先随机选一条过原点的直线,然后计算所有点到该直线的偏离程度(即误差)
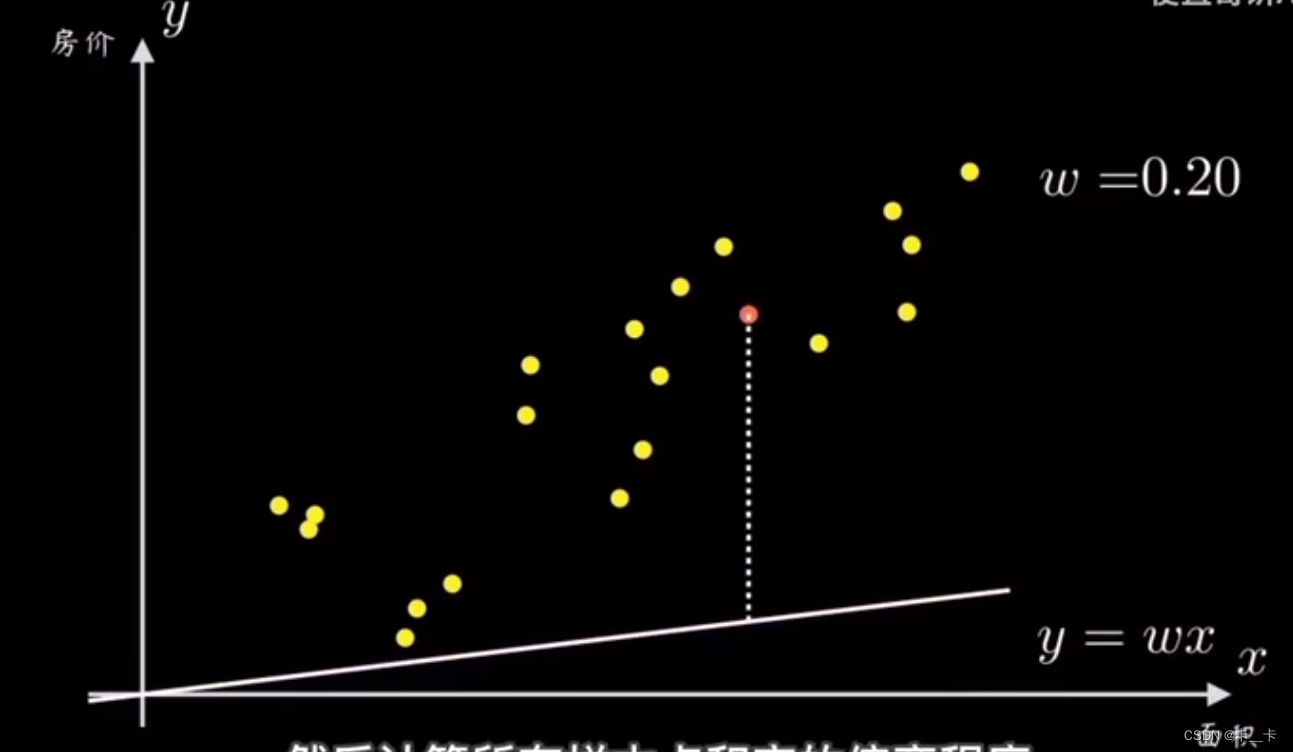
再根据误差大小调整直线的斜率w,这里的y=wx就是预测函数
2.损失函数(loss function)/代价函数(cost function)
对于一个点(x1,y1),误差e1=y1-wx1
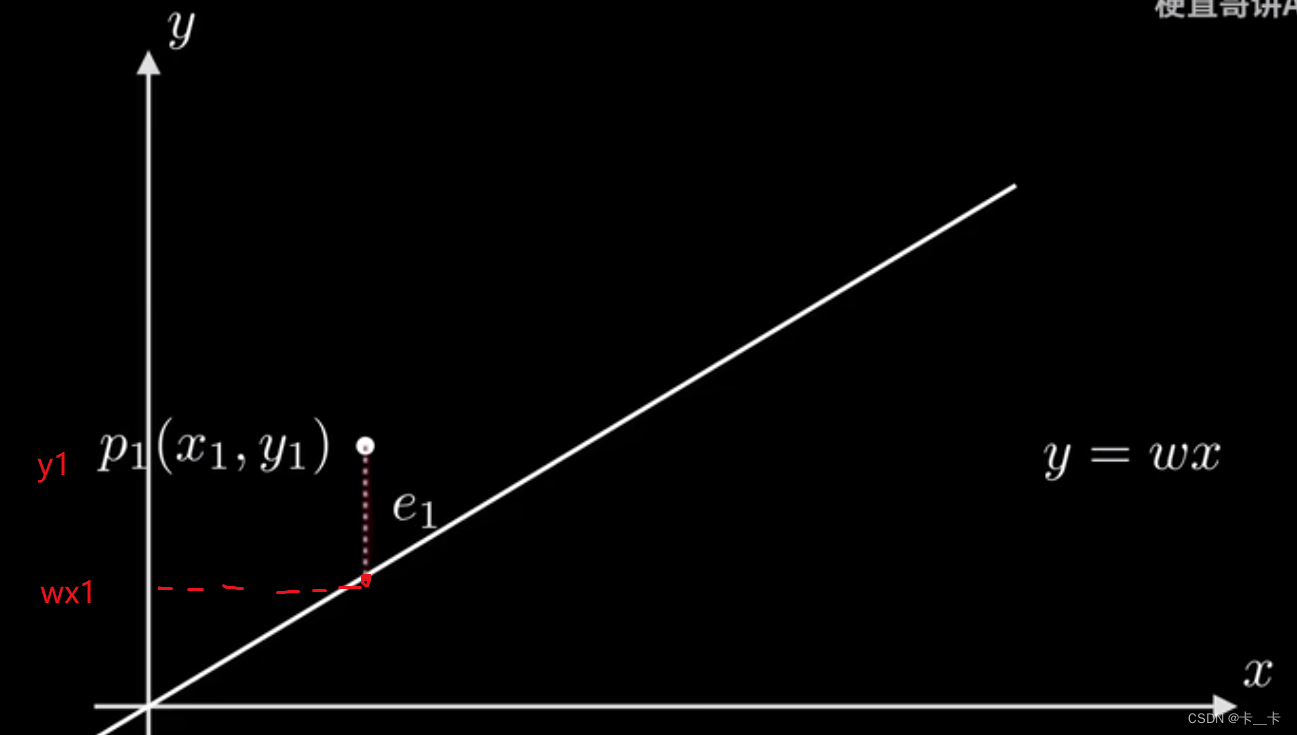
这里使用最小平方误差(Ordinary Least Squares, OLS),即将误差平方
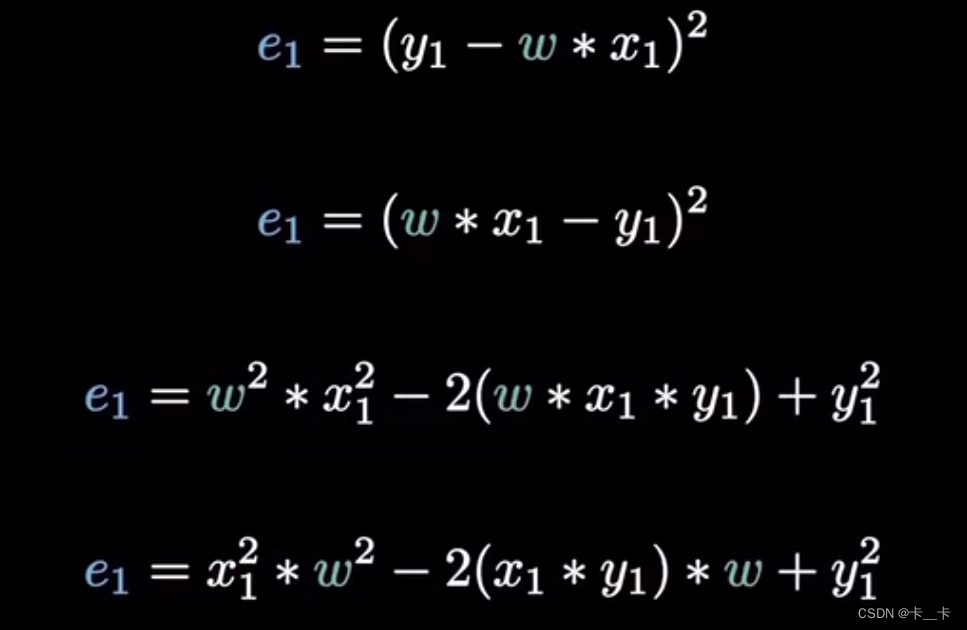
将所有点的误差平方再展开,其中x1,y1,n均为已知数
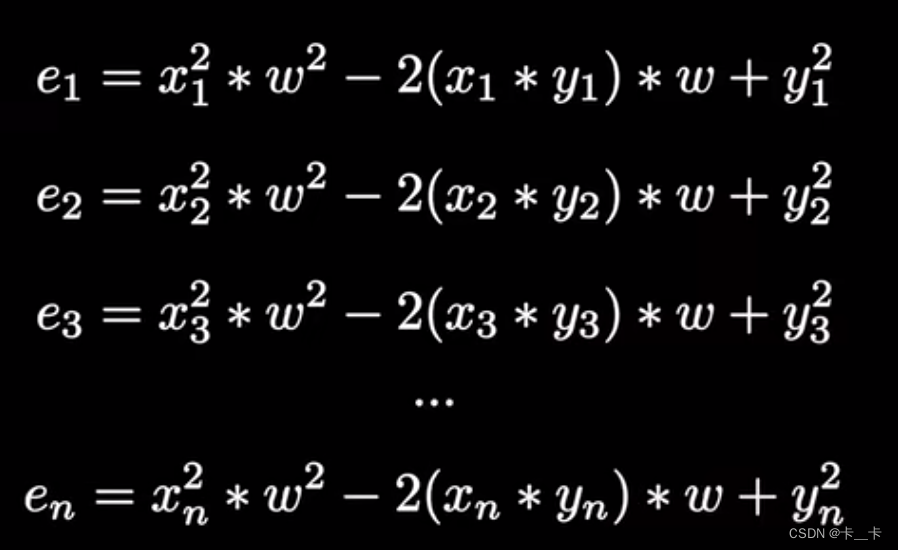
将其相加求平均,再合并同类项
其中a>0
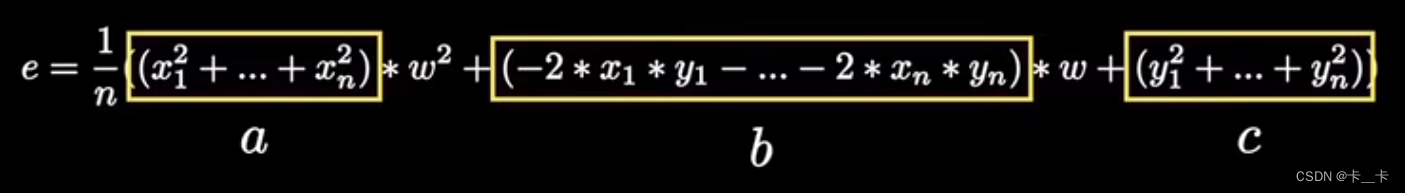
即可表示为
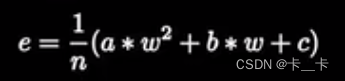
即代价函数cost/损失函数loss
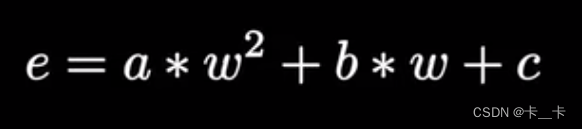
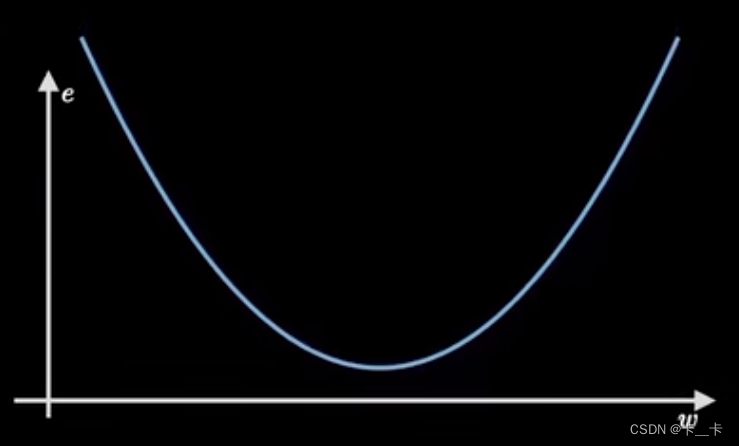
这样就完成了预测函数到代价函数的映射过程,随着左图w的增大,右图的点向右移动
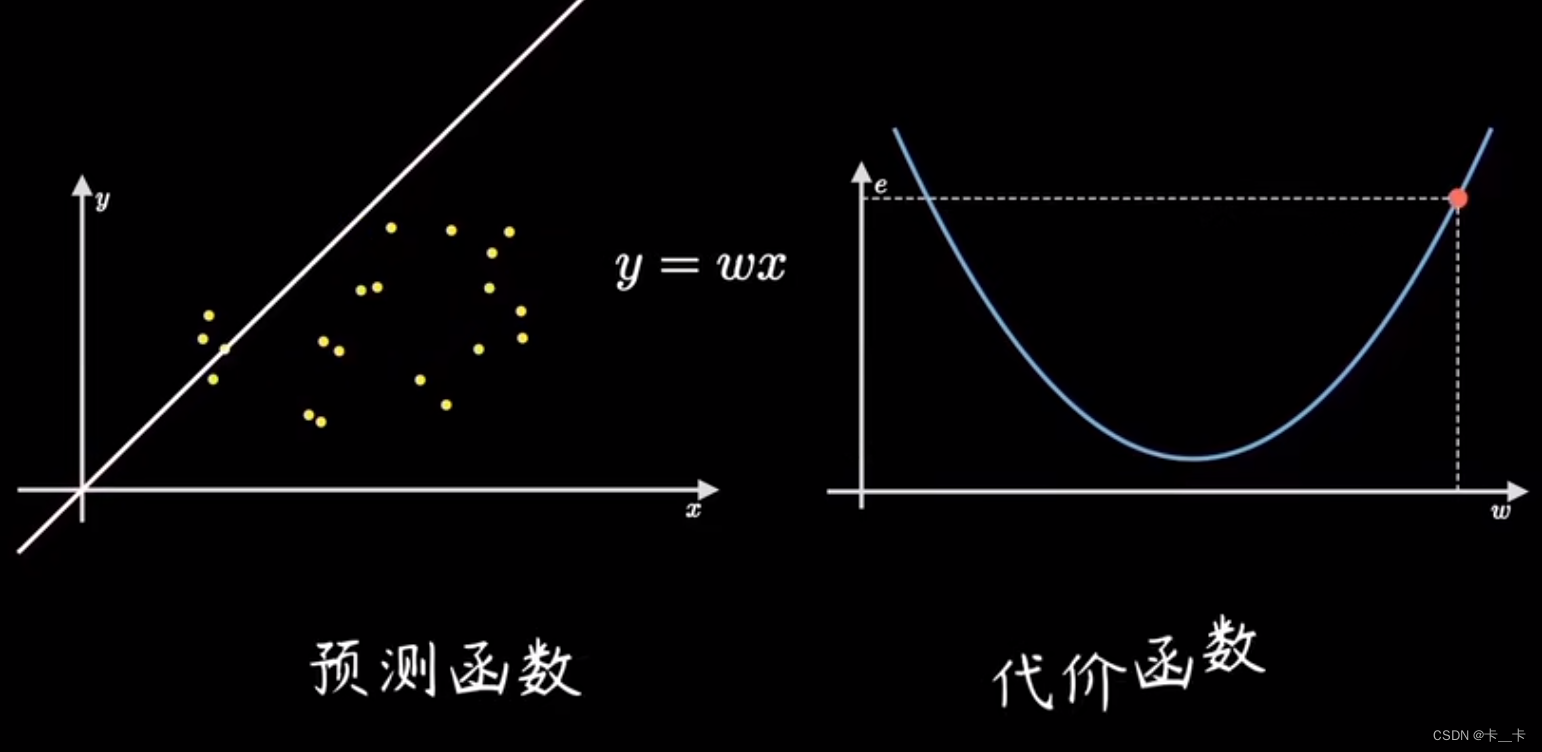
3.梯度计算
我们的目的是实现损失最小,即抛物线取得最小值时参数w的值
假设起始点在曲线上任意一处,寻找最低点的过程就是梯度下降
选择的下降方向是切线方向/梯度的反方向/陡峭程度最大的方向
梯度(gradient)是代价函数的导数
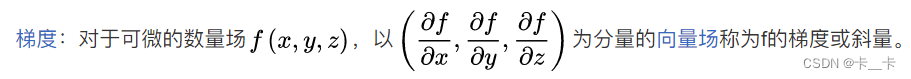
4.学习率(learning rate)
每一次更新参数利用多少误差, 就需要通过一个参数来控制, 这个参数就是学习率,也称为步长。
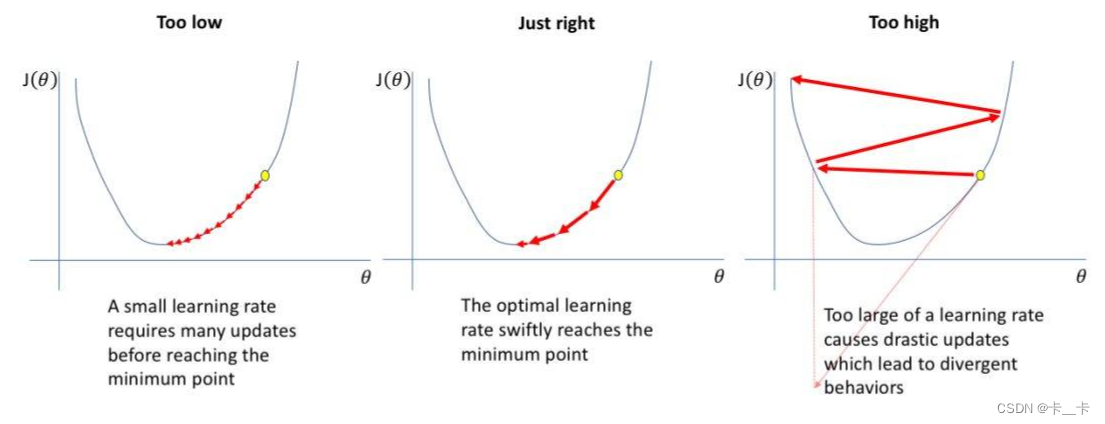
选择最优学习率是很重要的,因为它决定了我们是否可以迅速收敛到全局最小值。
小的学习率需要多次更新才能达到最低点,并且需要花费很多时间,且很容易仅收敛到局部极小值
学习率过大会导致剧烈的更新,可能总是在全局最小值附近,但是从未收敛到全局最小值
最佳学习率迅速达到最低点
每次新的w=旧的w-斜率*学习率
其中斜率=f导=梯度

循环迭代过程:定义代价函数→选择起始点→计算梯度→按学习率前进→计算梯度→按学习率前进→…到达最低点
二.线性回归(Linear Regression)
线性回归是一种统计学和机器学习中常用的预测方法,用于建立一个自变量(或称为特征)与因变量之间的线性关系模型。它假设自变量和因变量之间存在一个线性关系,并尝试通过拟合一条最佳拟合直线(或超平面)来进行预测。线性回归的目标是通过最小化预测值与实际观测值之间的差异(误差或残差)来找到最佳拟合直线或超平面。
在简单线性回归中,只有一个自变量和一个因变量之间的关系。这可以表示为一条直线的方程:y=wx+b
通过该预测函数我们可以得到误差 e=(wx+b-y)²
误差求和得到损失函数loss
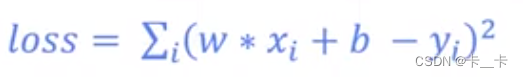
目的是找到最小loss(error)时w和b的值
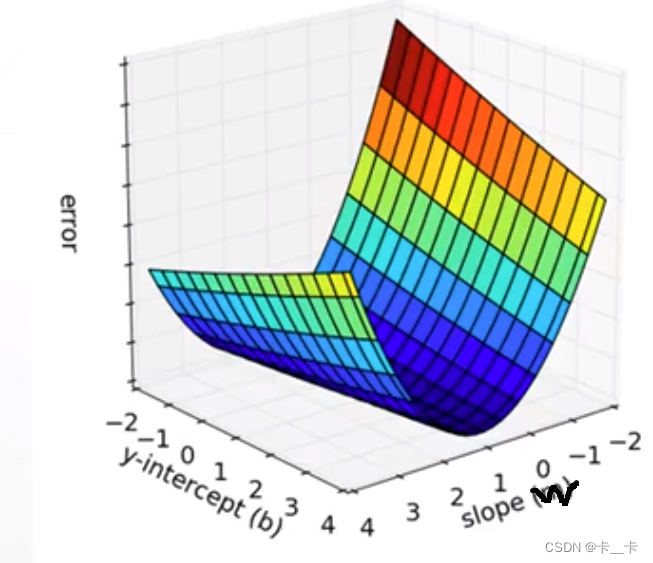
对于一个二元一次方程组,我们通常使用两式相减的方式求出参数b和w的值。这种可以精确求解的我们叫做闭合解(Closed-form Solution,也称封闭解)

但实际数据是有误差的,我们只能求得近似解
即实际的y=wx+b+ε,这里的ε叫做高斯噪声,由于高斯噪声的存在使得数据有误差
通过x和y的多组数据可以使结果更接近Closed-form Solution
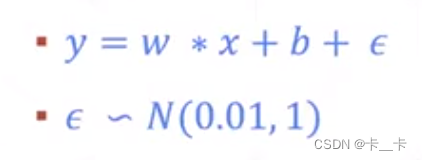
下面使用代码实现二元一次方程组的求解
数据下载:提取码:zn73
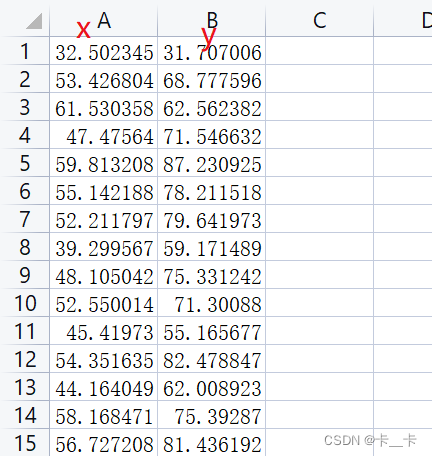
数据点集合的每一行表示一个数据点,第一列是自变量 xi,第二列是因变量 yi。
1.计算线性回归模型的误差函数
代码通过迭代遍历每个数据点,计算该数据点在回归模型下的预测值与实际观测值之间的误差。然后将每个误差的平方累加到总误差 totalError 中。最后,通过将总误差除以数据点的数量,计算出平均误差并返回。
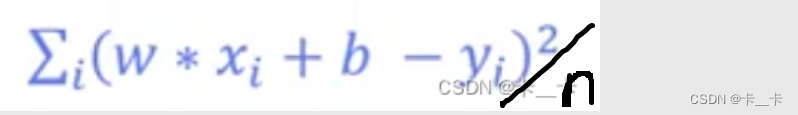
通过索引操作 points[i,0],我们可以获取第 i 个数据点的自变量 x 的值,因为它位于每行的第一列(索引为 0)
类似地,通过 points[i,1],我们可以获取第 i 个数据点的因变量 y 的值,因为它位于每行的第二列(索引为 1)
b: 回归模型的截距。
w: 回归模型的斜率。
points: 数据点的集合,其中每个数据点由自变量 x 和因变量 y 组成。
def compute_error_for_line_given_points(b,w,points):
totalError=0
for i in range(0,len(points)):
x=points[i,0]
y=points[i,1]
totalError+=(y-(w*x+b))**2
return totalError/float(len(points))
2.梯度下降中的参数更新
首先初始化截距梯度 b_gradient 和斜率梯度 w_gradient 为 0。然后,通过迭代遍历每个数据点,计算每个数据点对应的梯度值,以便在下一步更新中使用。对于每个数据点,根据当前的截距和斜率计算出预测值,然后根据预测值与实际观测值之间的误差来计算梯度。最后,将所有数据点的梯度累加到总梯度中,并除以数据点的数量 N,以获得平均梯度。接下来使用梯度下降的更新规则来更新截距和斜率。根据当前的截距和斜率值,分别减去学习率乘以对应的梯度,得到新的截距 new_b 和斜率 new_w。最后,将更新后的截距和斜率作为列表返回。

b_current: 当前的截距值。
w_current: 当前的斜率值。
points: 数据点的集合,其中每个数据点由自变量 x 和因变量 y 组成。
learningRate: 学习率,用于控制每次更新的步长。
def step_gradient(b_current,w_current,points,learningRate):
b_gradient=0
w_gradient=0
N=float(len(points))
for i in range(0,len(points)):
x=points[i,0]
y=points[i,1]
b_gradient+=(2*(w_current*x+b_current-y))/N # 对b偏导
w_gradient+=(2*(w_current*x+b_current-y)*x)/N # 对w偏导
new_b=b_current-learningRate*b_gradient
new_w=w_current-learningRate*w_gradient
return [new_b,new_w]
3.梯度下降算法的主要循环部分
points: 数据点的集合,其中每个数据点由自变量 x 和因变量 y 组成。
starting_b: 初始的截距值。
starting_w: 初始的斜率值。
learning_rate: 学习率,用于控制每次更新的步长。
num_iterations: 迭代次数,表示要运行梯度下降的步骤数。
import numpy as np
def gradient_decent_runner(points,starting_b,starting_w,learing_rate,num_iterations):
b=starting_b
w=starting_w
for i in range(num_iterations):
b,w=step_gradient(b,w,np.array(points),learing_rate)
return [b,w] # 返回最后一次迭代结果,即最终数据
4.运行
def run():
points=np.genfromtxt("data.csv",delimiter=",") # data.csv更换为文件的存放地址
learning_rate=0.0001
initial_b=0
initial_w=0
num_iterations=1000
print("Starting gradient descent at b={0},w={1},error={2}".format(initial_b,initial_w,compute_error_for_line_given_points(initial_b,initial_w,points)))
[b,w]=gradient_descent_runner(points,initial_b,initial_w,learning_rate,num_iterations)
print("After {0} interations b={1},w={2},error={3}".format(num_iterations,b,w,compute_error_for_line_given_points(b,w,points)))
这里的np.genfromtxt 是 NumPy 库中的一个函数,用于从文本文件加载数据并生成一个 NumPy 数组。该函数可以处理各种格式的文本数据,包括逗号分隔值(CSV)文件和具有不同分隔符的文件。
例如:存在一个名为 ‘data.csv’ 的 CSV 文件,其中的数据使用逗号作为分隔符。np.genfromtxt 函数将加载该文件的数据并生成一个 NumPy 数组,存储在变量 data 中,使用 print(data) 即可打印加载的数据。
import numpy as np
# 从名为 'data.csv' 的 CSV 文件中加载数据
data = np.genfromtxt('data.csv', delimiter=',')
# 打印加载的数据
print(data)
完整代码
import numpy as np
def compute_error_for_line_given_points(b,w,points):
totalError=0
for i in range(0,len(points)):
x=points[i,0]
y=points[i,1]
totalError+=(y-(w*x+b))**2
return totalError/float(len(points))
def step_gradient(b_current,w_current,points,learningRate):
b_gradient=0
w_gradient=0
N=float(len(points))
for i in range(0,len(points)):
x=points[i,0]
y=points[i,1]
b_gradient+=(2*(w_current*x+b_current-y))/N
w_gradient+=(2*(w_current*x+b_current-y)*x)/N
new_b=b_current-learningRate*b_gradient
new_w=w_current-learningRate*w_gradient
return [new_b,new_w]
def gradient_descent_runner(points,starting_b,starting_w,learing_rate,num_iterations):
b=starting_b
w=starting_w
for i in range(num_iterations):
b,w=step_gradient(b,w,np.array(points),learing_rate)
return [b,w]
def run():
points=np.genfromtxt("D:/Deep-Learning-with-PyTorch-Tutorials/lesson04-简单回归案例实战/data.csv",delimiter=",")
learning_rate=0.0001
initial_b=0
initial_w=0
num_iterations=1000
print("Starting gradient descent at b={0},w={1},error={2}".format(initial_b,initial_w,compute_error_for_line_given_points(initial_b,initial_w,points)))
[b,w]=gradient_descent_runner(points,initial_b,initial_w,learning_rate,num_iterations)
print("After {0} interations b={1},w={2},error={3}".format(num_iterations,b,w,compute_error_for_line_given_points(b,w,points)))
run()
运行结果