力扣题目：#509. 斐波那契数 

刷题时长：参考答案后5min

解题方法：动态规划

复杂度分析

• 时间O(n)
• 空间O(n)

问题总结

无

本题收获

• 动规五部曲思路
  • 确定dp数组以及下标的含义：dp[i]的定义为，第i个数的斐波那契数值是dp[i]
  • 确定递推公式：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
  • dp数组初始化：dp[0] = 0; dp[1] = 1;
  • 确定遍历顺序：递归公式中dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的
  • 举例推导dp数组：当N为10的时候，dp数组应该为数列 0 1 1 2 3 5 8 13 21 34 55

---

力扣题目：#70. 爬楼梯 

刷题时长：5min

解题方法：动规

复杂度分析

• 时间O(n)
• 空间O(n)

问题总结

• dp数组初始化索引变化，for循环需随之变化

本题收获

• 练习了空间O(1)的解法，无需维护dp数组，只要维护curr，pre1，pre2
• 动规思路
  • 确定dp数组以及下标的含义：爬到第i层楼梯，有dp[i]种方法
  • 确定递推公式：dp[i] = dp[i - 1] + dp[i - 2] 
  • dp数组初始化：dp[1] = 1，dp[2] = 2，然后从i = 3开始递推
  • 确定遍历顺序：从前向后
  • 举例推导dp数组：同斐波那契数列

---

力扣题目： #746. 使用最小花费爬楼梯 

刷题时长：参考题解后5min

解题方法：动规

复杂度分析

• 时间O(n)
• 空间O(n)

问题总结

• 递推公式只基于了cost，没用到dp之前的状态
• 注意顶楼的定位不是cost数组的末位，而是cost数组末位的后一位
•  到达第 0个台阶是不花费的，但从第0个台阶往上跳的话，需要花费 cost[0]

本题收获

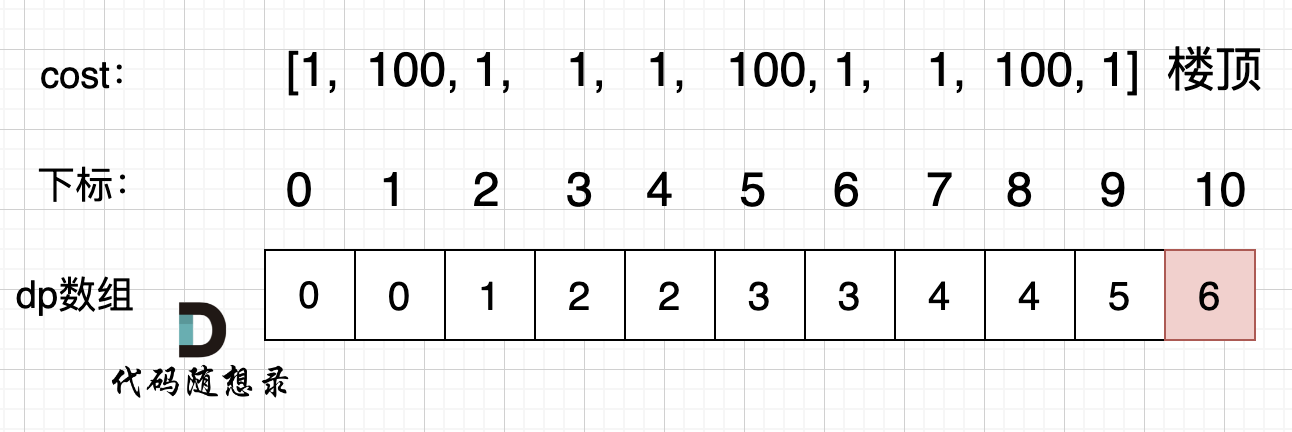
• 确定dp数组以及下标的含义：到达第i台阶所花费的最少体力为dp[i]
• 确定递推公式：dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
• dp数组初始化：dp[0] = 0，dp[1] = 0. 到达第0个台阶是不花费的，但从第0个台阶往上跳的话，需要花费cost[0]
• 确定遍历顺序：从前向后
• 举例推导dp数组：测试案例2举例如下