1.简述
降维:
比如现在有100维的变量来表征一个东西,我们觉得太冗余复杂了,想降低到10维。但是我们没有确定的筛选依据,直接使用数学工具来实现降维,就好像丢进了一个黑箱,经过抽象、提炼,得到了新的10维特征,这新的10维特征可能失去了物理意义,我们也不知道它们具体是怎么来的,表征什么,但是确实是可以用它们表征这个东西,而且是经过了原先100维特征的信息的融合、取舍过程。它的过程是比较高级的。
特征选择:
选择出100维特征里面最重要的10个特征,这个筛选过程是有依据的。比如苹果有很多特征, 大小,形状,颜色,味道,生长季节,……。我们选择:颜色红、味道甜等几个非常明显的重要的特征出来就足以表示苹果了。当然,颜色和味道可能也有一定的耦合关系,生成地点、时间也有耦合关系,如果懒得管特征之间的耦合关系,直接丢进降维的黑箱中,也可以得到新的几个降维后的特征,但我们可能就说不出这个特征的含义了,只是一些数据信息而已了。
偏最小二乘法(Partial Least Squares, PLS)
解决了PCA中不足的地方。
• PCA方法提取出的前若干个主成分携带了原输入变量矩阵的大部分信息,消除了相互重叠部分的信息。但没有考虑主成分对输出变量的解释能力,方差贡献率很小但对输出变量有很强解释能力的主成分将会被忽略掉,这无疑会对校正模型的性能产生一定的影响。偏最小二乘法(PLS)可以很好地解决这个问题。
• PLS的基本思路是逐步回归,逐步分解输入变量矩阵和输出变量矩阵,并综合考虑提取的主成分对输入变量矩阵和输出变量矩阵的解释能力,直到满足性能要求为止。
偏最小二乘作为一种线性的、有监督的、基于回归的数据降维工具,跟LDA倒是同卵双生、联系紧密,对比前篇中提到的“LDA是一种线性的、基于分类的、监督学习的数据降维工具”。
这个方法的核心跟“最小二乘”技术倒是没有关联,方法的重点不是在“最小二乘”上,关键是在于降维,跟LDA有几分神似。在二分类问题里,把PLS当成LDA做降维也没啥大问题
PLS这套方法有不同领域的人再使用,符号也不一致,可能也影响了方法的推广,没有达到PCA这种人尽皆知的程度。
偏最小二乘法(Partial Least Square)的知名度貌似远远没有PCA(主成分分析),甚至没有LDA(线性判别分析)高,可能就在于这个名字中的“最小二乘”,这个方法跟最小二乘的有点关系,但不是核心,如果名字叫什么“一种基于线性回归的降维方法”之类的就容易理解了。而且,PLS这个名字是一类方法的总称,至少包含了两大方法:
- PLS1,响应变量本质是1维的,即使是多维,也当做多个单维进行处理
- PLS2,响应变量多维同时处理,这里还分得分矩阵是否正交,又产生了不同的算法。。
2.代码
%% I. 清空环境变量 偏最小二乘
clear all
clc
%% II. 导入数据
load spectra;
%% III. 随机划分训练集与测试集
temp = randperm(size(NIR, 1));
% temp = 1:60;
%%
% 1. 训练集——50个样本
P_train = NIR(temp(1:50),:);
T_train = octane(temp(1:50),:);
%%
% 2. 测试集——10个样本
P_test = NIR(temp(51:end),:);
T_test = octane(temp(51:end),:);
%% IV. PLS回归模型
%%
% 1. 创建模型
k = 2; %主成分设置为2
[Xloadings,Yloadings,Xscores,Yscores,betaPLS,PLSPctVar,MSE,stats] = plsregress(P_train,T_train,k);
%%
% 2. 主成分贡献率分析
figure
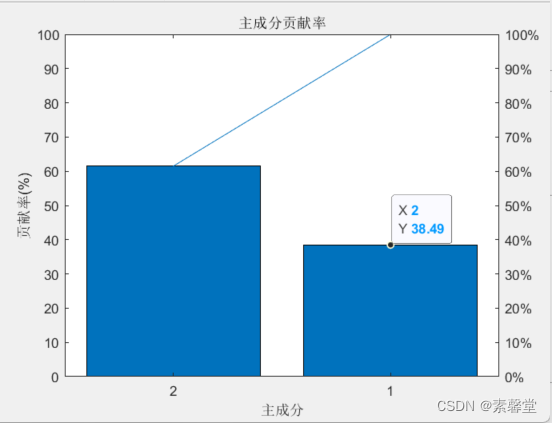
percent_explained = 100 * PLSPctVar(2,:) / sum(PLSPctVar(2,:));
pareto(percent_explained)
xlabel('主成分')
ylabel('贡献率(%)')
title('主成分贡献率')
%%
% 3. 预测拟合
N = size(P_test,1);
T_sim = [ones(N,1) P_test] * betaPLS;
%% V. 结果分析与绘图
%%
% 1. 相对误差error
error = abs(T_sim - T_test) ./ T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));
%%
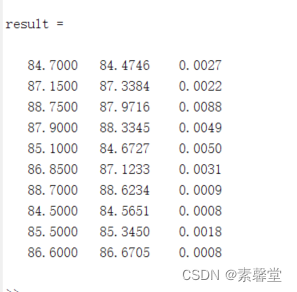
% 3. 结果对比
result = [T_test T_sim error]
%%
% 4. 绘图
figure
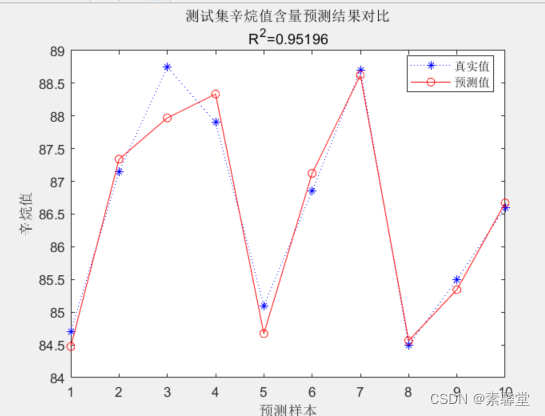
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值','location','best')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)
3.运行结果