13.4.1 何为二分查找？

我们已经学完了Python中的字典和集合，利用字典和集合就可以实现快速查找，非常方便。字典与集合使用了哈希表的索引结构来加快查找，对于列表这种顺序表结构，又该如何优化查找性能呢？在本节教程中，我们会学习数据结构与算法这门课程中的一个非常经典的查找算法:二分查找。

利用二分查找即可大幅提升顺序表的查找性能。

二分查找的核心原理:先对数据集合进行排序，然后每次与中间位置的元素进行比较，相等则直接返回，不相等则根据数据集合升序或降序来查找另外一半区间。二分查找的查找过程如下图所示：

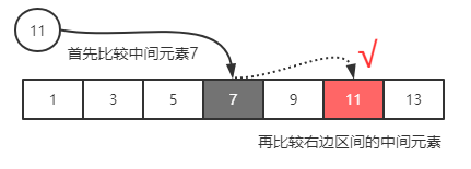
(1) 首先比较中间元素，11比7大，由于数据集合是升序，所以下次查找右边区间

(2) 不断重复这样的过程，直到执行完所有查找

13.4.2 算法实现

我们现在来实现这个二分查找算法:

"""
@author: 薯条老师
@desc: 实现二分查找算法
"""

import random
# 使用random模块的randint方法生成随机数，使用列表推导式来构造随机数列表
numbers = [random.randint(1, 7) for _ in range(5)]

# 实现二分查找算法之前得先对列表进行排序，我们现使用冒泡排序来排序numbers
length_of_numbers = len(numbers)
for outer_index in range(length_of_numbers-1):
    for inner_index in range(length_of_numbers-1-outer_index):
        if numbers[inner_index] > numbers[inner_index+1]:
            numbers[inner_index], numbers[inner_index+1] = \
                numbers[inner_index+1], numbers[inner_index]
                
print(f"已排序的列表:{numbers}")

# element表示要查找的元素
element = 5
# left表示区间的起始位置，right表示区间的结束位置
left, right = 0, length_of_numbers-1
while left < right:
    # 将起始位置与结束位置相加，再整除2，即可得到中间位置
    mid = (left+right) // 2
    if numbers[mid] == element:
        print(f"{element}位于numbers列表的第{mid}个位置")
        break
    elif numbers[mid] > element:
        # 当中间元素大于查找的元素时，说明只能往左半边区间进行查找
        # 因为列表是升序排列，中间的比查找的大，那右区间的都比查找的元素大
        # 左边的区间的起始位置不需要边，结束位置是中间位置前一个位置，
        # 所以为什么right = mid-1
        right = mid-1
    else:
        # 当中间元素小于查找的元素时，说明只能往右半边区间进行查找
        # 所以为什么是left = mid+1
        left = mid+1