导数
导数就是表示某个瞬间的变化量,式子如下:
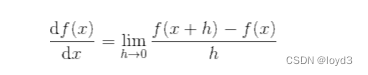
式子的左边,表示f(x)关于x的导数,即f(x)相对于x的变化程度。式子表示的导数的含义是,x的“微小变化”将导致函数f(x)的值在多大程度上发生变化。其中,表示微小变化h无限趋近0。
下面使用程序来实现上面的例子
def numerical_diff(f,x):
h = 10e - 50
return (f(x+h) - f(x))/h
这个函数有两个参数,即“函数f”和“传给函数f的参数x”
上面的函数乍一看没什么问题,但是实际上这段代码有两个需要改进的地方
- h使用了10e-50这个微小值。但是,这样反而产生了舍入误差(rounding error)。所谓舍人误差,是指因省略小数的精细部分的数值(比如小数点后第8位以后的数值)而造成最终的计算结果上的误差。如果用float32类型(32位的浮点数)来表示10e-50,就会变成0.0,无法正确表示出来。因此需要将微小值h改为。使用0.0001就可以得到正确的结果。
- 第二个要改进的地方与函数f的差分有关。上述实现中计算了函数f在x+h和x之间的差分,但这个计算有误差,因为“真的导数”对应函数在x处的斜率(称为切线),但上述实现中计算的导数对应的是(x+h)和x之间的斜率。这个差异出现是因为h不可能无限接近0。为了减少这个误差,可以以x为中心,计算它左右两边的差分,所以也称为中心差分。(x + h)和x之间的差分称前向差分。
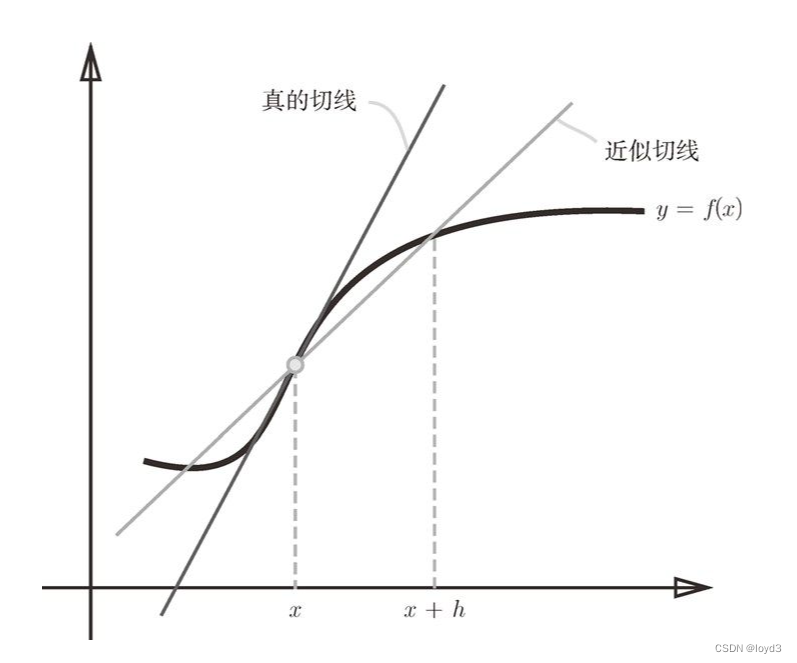
看下面是改进的代码:
def numerical_diff(f,x):
h = 1e-4 #0.001
return (f(x+h) - f(x-h))/ 2*h
利用微小的差分求导数的过程称为数值微分(numerical differentiation)
基于数学式的推导求导数的过程,称为“解析性求解”或者“解析性求导”
解析性求导得到的导数是不含误差的“真的导数”。
偏导数
有多个变量的函数的导数称为偏导数。
例如这个例子:
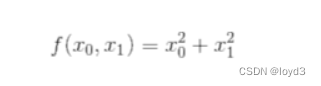
这个式子可以用Python来实现,如下所示
def function_2(x):
return x[0]**2 + x[1]**2
# 或者 return np.sum(x**2)
这里,假定想参数输入了一个NumPy数组,函数的内部实现比较简单,先计算 NumPy 数组中各个元素的平方,再求它们的和。下面是这个函数的图像:
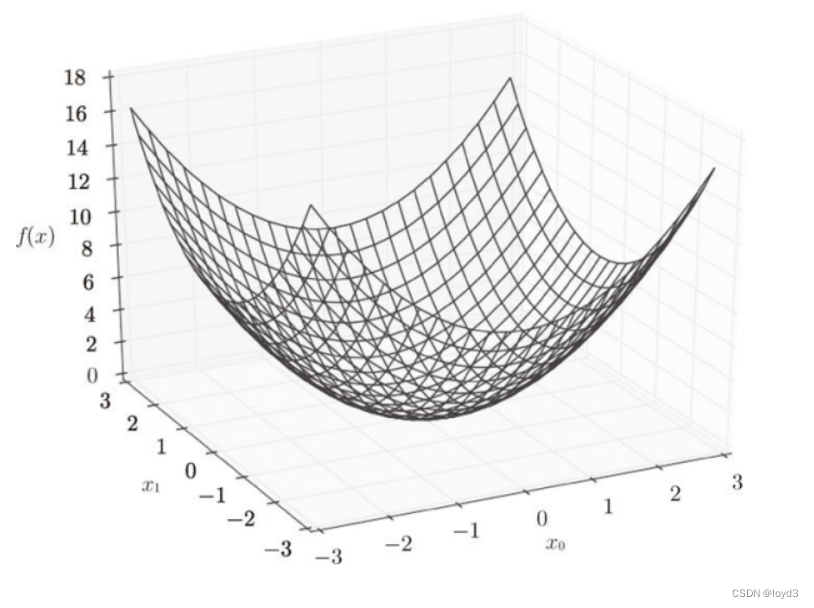
求这个式子的导数,这里需要注意的是,这个式子有两个变量,所以有必要区分对哪个变量求导数。
求x0=3,x1=4时,关于x0的偏导数
>>>def function tmp1(x0):
... return x0*x0+4.0**2.0
...
>>> numerical_diff(function_tmp1, 3.0)
结果:600000000000378
求x0=3,x1=4时,关于x1的偏导数
>>>def function tmp1(x0):
... return 3.0**2.0+x1*x1
...
>>> numerical_diff(function_tmp2, 4.0)
结果:7.999999999999119
这里的结果和解析解的导数基本一致。
像这样,偏导数和单变量的导数一样,都是求某个地方的斜率。
偏导数需要将多个变量中的某一个变量定为目标变量,并将其他变量固定为某个值。
梯度
由全部变量的偏导数汇总而成的向量称为梯度(gradient)。
梯度可以像下面这样来实现
def numerical_gradient(f,x):
h = 1e - 4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) /(2*h)
x[idx] = tmp_val # 还原值
return grad
在该函数中,参数f为函数,x为NumPy数组
然后用这个方法来求点(3,4)、(0,2)、(3,0)处的梯度
可以得到:
点(3,4)处的梯度是(6,8),点(0.2)处的梯度是(0,4),点(3,0)处的梯度是(6,0)。
如果把函数的所有梯度(元素值为负梯度)都显示出来会发现梯度指向函数的“最低处”(最小值)。然而并不是任何时候梯度都会指向最低处,实际上,梯度会指向各点处的函数值降低的方向。更严格地讲,梯度指示的方是各点处的函数值减小最多的方向。
梯度法
神经网络也必须在学习时找到最优参数(权重和偏置)。这里所说的最优参数是指损失函数取最小值时的参数,这里通过巧妙地使用梯度来寻找函数最小值(或者尽可能小的值)的方法就是梯度法。
这里需要注意的是,梯度表示的是各点处的函数值减小最多的方向。因此,无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上,在复杂的函数中,梯度指示的方向基本上都不是函数值最小处
函数的极小值、最小值以及被称为鞍点(saddle point)的地方,梯度为0。鞍点是从某个方向上看是极大值,从另一个方向上看则是极小值的点。虽然梯度法是要寻找梯度为0的地方,但是那个地方不一定就是最小值(也有可能是极小值或者鞍点)。(梯度为0的地方,不一定就是最小值)
此外,当函数很复杂且呈扁平状时,学习可能会进入一个(几乎)平坦的地区,陷入被称为“学习高原”的无法前进的停滞期。
虽然梯度的方向并不一定指向最小值,但沿着它的方向能够最大限度地减小函数的值。因此,在寻找函数的最小值(或者尽可能小的值)的位置的任务中,要以梯度的信息为线索,决定前进的方向。
(要以梯度为学习的前进方向)
通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法
下面用数学式来表示梯度法,如下所示:
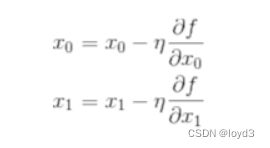
其中n表示更新量,在神经网络的学习中,称为学习率。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。
学习率需要事先确定为某个值,比如0.01或0.001。一般而言,这个过大或过小,都无法抵达一个“好的位置”。在神经网络的学习中,一般会边改变学习率的值,一边确认学习是否正确进行了。
学习率过大的话,会发散成一个很大的值;反过来,学习率过小的话,基本上没怎么更新就结束了。
像学习率这样的参数称为超参数,超参数需要尝试多个值,以便找到一种可以使学习顺进行的设定。
下面用Python来实现梯度下降法。
def gradient_descent(f,init_x,lr=0.01,step_num=100):
x=init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr*grad
return x
init_x是初始值,lr是学习率learnirate,step_num是梯度法的重复次数
使用这个函数可以求函数的极小值,顺利的话,还可以求函数的最小值。
神经网络的梯度
神经网络的梯度是指损失函数关于权重参数的梯度。
比如,有一个只有一个形状为2 x 3的权重 W的神经网络,损失函数用L表示。此时,梯度可以用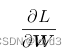 表示
表示
用数学式表示的话,如下所
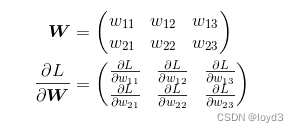
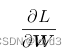 的元素由各个元素关于W的偏导数构成。比如,第1行第1列的元素
的元素由各个元素关于W的偏导数构成。比如,第1行第1列的元素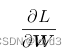 表示当W11稍微变化时,损失函数L会发生多大变化。这里要注意的是形状要和W相同
表示当W11稍微变化时,损失函数L会发生多大变化。这里要注意的是形状要和W相同
下面,我们以一个简单的神经网络为例,来实现求梯度的代码。
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient
class simpleNet:
def __init__(self):
# 实例变量, 形状为2x3的权重参数
self.W = np.random.randn(2,3) # 用高斯分布进行初始化
# 用于预测
def predict(self, x):
return np.dot(x, self.W)
# 求损失函数值,这里参数x接收输人数据,t接收正确解标签
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
# Python中如果定义的是简单的函数,可以使用lambda表示法
# 对应的方法其实是
# def f(W):
# return net.loss(x,t)
# 这里面参数W是一个伪参数,因为numerical_gradient会在内部执行f(x),为了与之兼容定义f(W)
f = lambda w: net.loss(x, t)
# 使用numerical_gradient求梯度
# net.W 权重参数
dW = numerical_gradient(f, net.W)
print(dW)
求出神经网络的梯度后,接下来只需根据梯度法,更新权重参数即可。