Leetcode
- Leetcode -563.二叉树的坡度
- c
Leetcode -563.二叉树的坡度
题目:给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例 1:
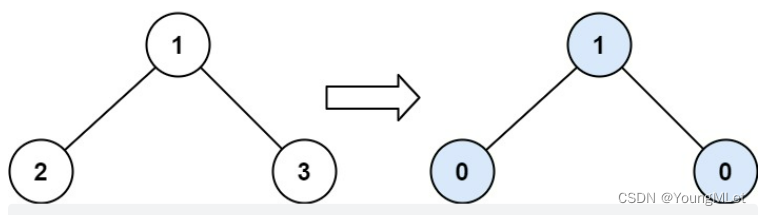
输入:root = [1, 2, 3]
输出:1
解释:
节点 2 的坡度: | 0 - 0 | = 0(没有子节点)
节点 3 的坡度: | 0 - 0 | = 0(没有子节点)
节点 1 的坡度: | 2 - 3 | = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 )
坡度总和:0 + 0 + 1 = 1
示例 2:
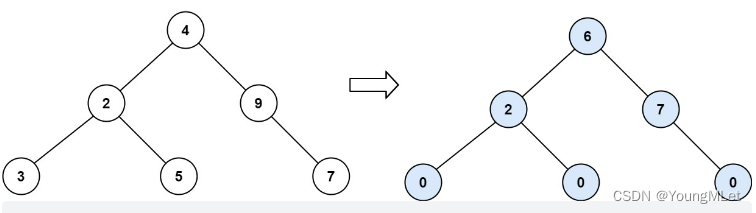
输入:root = [4, 2, 9, 3, 5, null, 7]
输出:15
解释:
节点 3 的坡度: | 0 - 0 | = 0(没有子节点)
节点 5 的坡度: | 0 - 0 | = 0(没有子节点)
节点 7 的坡度: | 0 - 0 | = 0(没有子节点)
节点 2 的坡度: | 3 - 5 | = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 )
节点 9 的坡度: | 0 - 7 | = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 )
节点 4 的坡度: | (3 + 5 + 2) - (9 + 7) | = | 10 - 16 | = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 )
坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
示例 3:
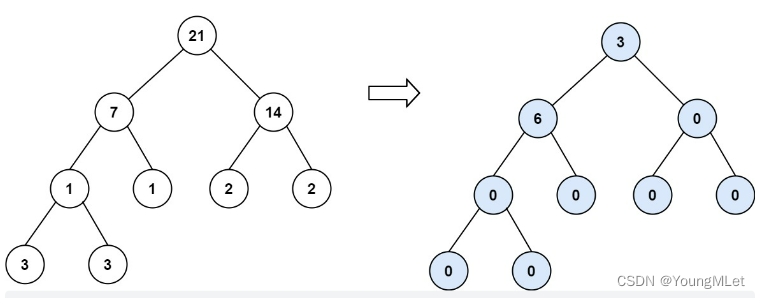
输入:root = [21, 7, 14, 1, 1, 2, 2, 3, 3]
输出:9
提示:
树中节点数目的范围在[0, 10^4] 内
- 1000 <= Node.val <= 1000
思路:化为子问题用变量 ans 记录左子树和右子树每个节点的坡度;结束条件,如果为空,就返回0;如果不为空,就继续递归其左子树和右子树,计算其左子树与右子树的和;如果不为空,返回其左子树或右子树的和;
int dfs(struct TreeNode* root, int* ans)
{
if (root == NULL)
return 0;
//左右子树节点
int leftTree = dfs(root->left, ans);
int rightTree = dfs(root->right, ans);
//该节点的坡度
*ans += abs(leftTree - rightTree);
//返回左右子树的和,和该根的 val
return leftTree + rightTree + root->val;
}
int findTilt(struct TreeNode* root)
{
// ans 记录二叉树的坡度
int ans = 0;
dfs(root, &ans);
return ans;
}
c
题目:编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。
建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
示例1
输入:
abc##de#g##f###
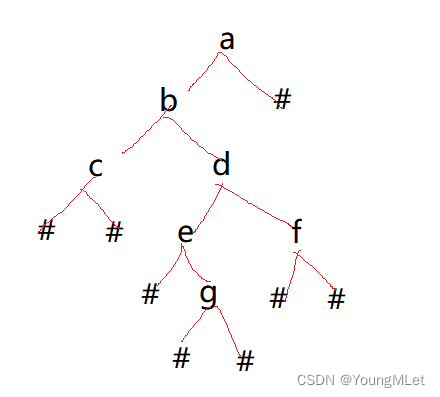
输出:
c b e g d f a
思路:因为字符串是按照前序遍历得到的,所以我们也按照先创建根的节点,再创建其左右子树的节点,最后将它们连接起来;最后创建完二叉树后,按照中序遍历打印数据;
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef char BTDataType;
//节点的结构体
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
//创建新的节点
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
assert(newnode);
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
//创建二叉树
BTNode* CreatTree(BTDataType* a, int* pi)
{
//如果是 # ,就返回空
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//如果不为空,就创建该字符的节点,pi往后遍历后面的字符
BTNode* root = BuyNode(a[(*pi)++]);
//将节点的左右子树连接起来
root->left = CreatTree(a, pi);
root->right = CreatTree(a, pi);
//返回根
return root;
}
//打印中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
int main()
{
char a[100];
scanf("%s", &a);
int i = 0;
//i遍历字符串
BTNode* root = CreatTree(a, &i);
InOrder(root);
return 0;
}