AVL树原理以及插入代码讲解（插入操作画图~细节）

news2024/11/28 4:41:29

原理

AVL 树是一种平衡搜索二叉树，得名于其发明者的名字（ Adelson-Velskii 以及 Landis）。（可见名字长的好处，命名都能多占一个字母出来）。在搜索树的前提下平衡搜索二叉树还定义如下：

  1. 左右子树的高度差小于等于 1。
  2. 其每一个子树均为平衡二叉树。

我们以SGI版本AVL树

先来查看树中每个结点内容。

template<class K,class V>
	struct AVLTreeNode
	{
		AVLTreeNode* _left;//左子树
		AVLTreeNode* _right;//右子树
		AVLTreeNode* _parent;//父节点
		pair<K, V> _kv;//数据存储内容
		int _bf;//平衡因子

		AVLTreeNode(pair<K, V>kv=pair<K, V>())//默认赋值构造
			:_kv(kv)
			, _left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			,_bf(0)
		{}
	};

左子树与右子树指针我们不做过多介绍。

我们存储AVL树是一种存储key_value数据的树，所以我们使用pair库中类型存储数据。

让我们看看平衡因子是什么：

平衡因子

某个结点的右子树的高度减去左子树的高度得到的差值。

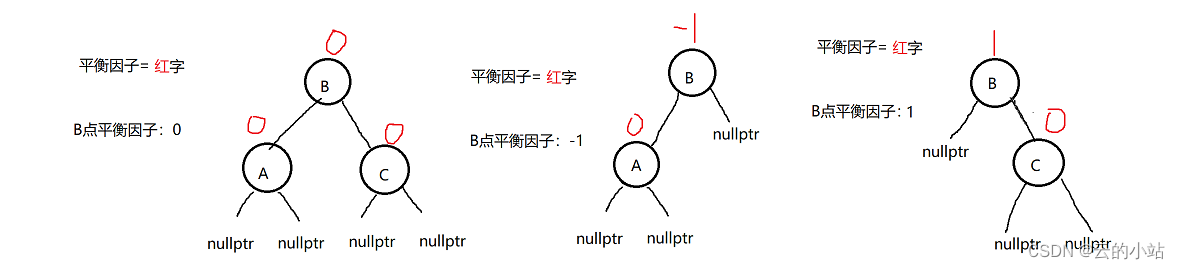
平衡因子在[-1,1]之间都是属于平衡的平衡搜索二叉树，每个结点都需要符合这个要求

在插入的过程中我们会破坏平衡，这个时候就需要对树结点进行转至操作。

AVL树的插入insert

和普通搜索二叉树一样，先要寻找插入的位置。

        bool Insert(const pair<K, V>& kv)
		{
			if (_root == nullptr)
			{
				_root = new Node(kv);
			}
			else
			{
				Node* parent = nullptr;//保存上级指针，我们链接都是cur走到空指针创建结点给cur
                                       //但是这个新的结点需要被链接到树中，我们不可以对
                                       //nullptr进行访问上级的数据，所以我们必须留一个parent            
                                       //用来链接新的结点。
				Node* cur = _root;
				while (cur)
				{
					parent = cur;
					if (cur->_kv.first > kv.first)
					{
						cur = cur->_left;//新数据小于当前数据，向cur的左边走
					}
					else if (cur->_kv.first < kv.first)
					{
						cur = cur->_right;//新数据大于当前数据，向cur的右边走
					}
					else
					{
						return false;//数据相同退出，并返回false
					}
				}
				cur = new Node(kv);//cur到了nullptr，创建新的结点。
                
                //新结点链接到树
				if (parent->_kv.first <cur->_kv.first)
				{
					parent->_right = cur;
				}
				else
				{
					parent->_left = cur;
				}
				cur->_parent = parent;//处理新结点的_parent

插入结点后我们需要修改平衡因子，确保插入数据后我们的树依旧是AVL树。

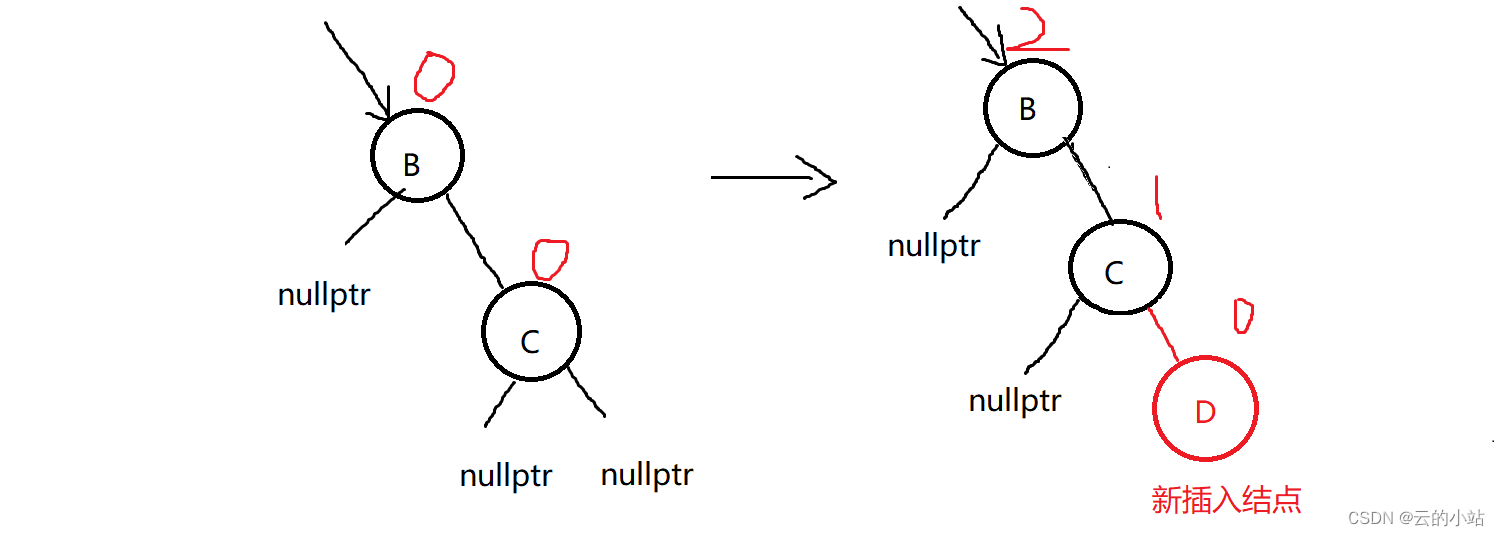
 更新平衡因子规则:

  1.  新增在右，parent->bf+ +;新增在左，parent->bf--;
  2. 更新后，parent->bf == 1 or -1，说明parent插入前的平衡因子是0，说明左右子树高度相等，插入后有一边高，parent高度变了，该节点插入稍稍改变平衡，需要继续往上更新平衡因子。
  3. 重新后，parent->bf == 0说parent插入前的平衡因子是1 or -1，说明左右子树一边高一边低，插入后两边一样高，插入填上了矮了那边，parent所在子树高度不变，不需要继续往上更新
  4. 更新后，parent->bf == 2 or -2，说明parent插入前的平衡因子是1 or -1，已经平衡临界值，插入变成2 or -2，打破平衡，parent所在子树需要旋转处理
  5. 更新后，parent->bf > 2 r< -2的值，不可能，如果存在，则说明插入前就不是AVL树，需要去检查之前操作的问题，不需要再去考虑现在代码的问题了。
while (parent)
{

	if (parent->_right == cur)//根结点(praent)的右子树(cur)插入了一个结点当前根结点平衡因子++
	{
		++parent->_bf;
	}
	else /*if()  可以不写这个*///根结点(praent)的左子树(cur)插入了一个结点当前根结点平衡因子--
	{
		--parent->_bf;
	}
	if (parent->_bf == 0)//修改更新平衡因子后，查看当前平衡因子，为0代表根补齐了该根的低子树
                         //parent所在子树高度不变，不需要继续往上更新
	{
		break;
	}
	else if (abs(parent->_bf) == 1)//parent原本为0的平衡因子被改变，高度变高了，parent左右被
                                   //该节点插入稍稍改变平衡，需要继续往上更新平衡因子。
	{
		cur = parent;
		parent = parent->_parent;
	}
	else if (abs(parent->_bf) == 2)//说明parent插入前的平衡因子是1 or -1，已经平衡临界值，插
                                   //入变成2 or -2，打破平衡，parent所在子树需要旋转处理
	{
        //平衡被破坏。
	}
	else
	{
		std::cout << "AVL fail\n";
		assert(false);
	}
}

 这既是转至：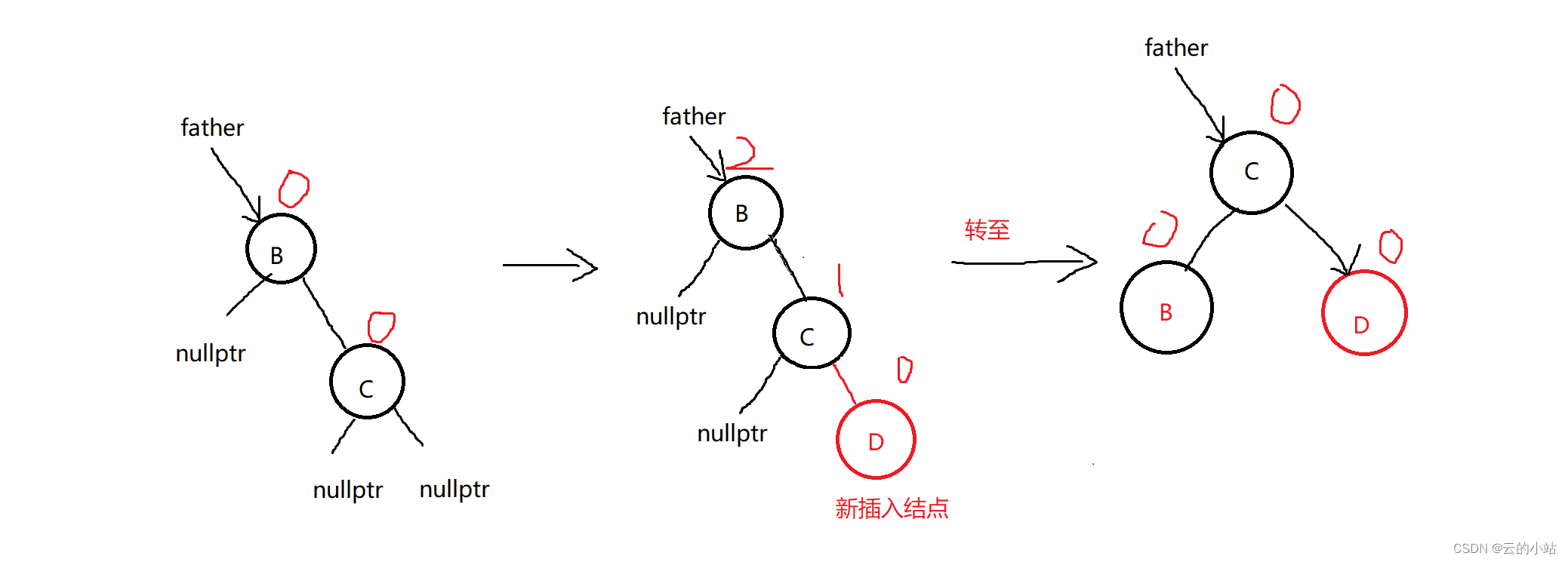

但是不平衡的情况有无数种。

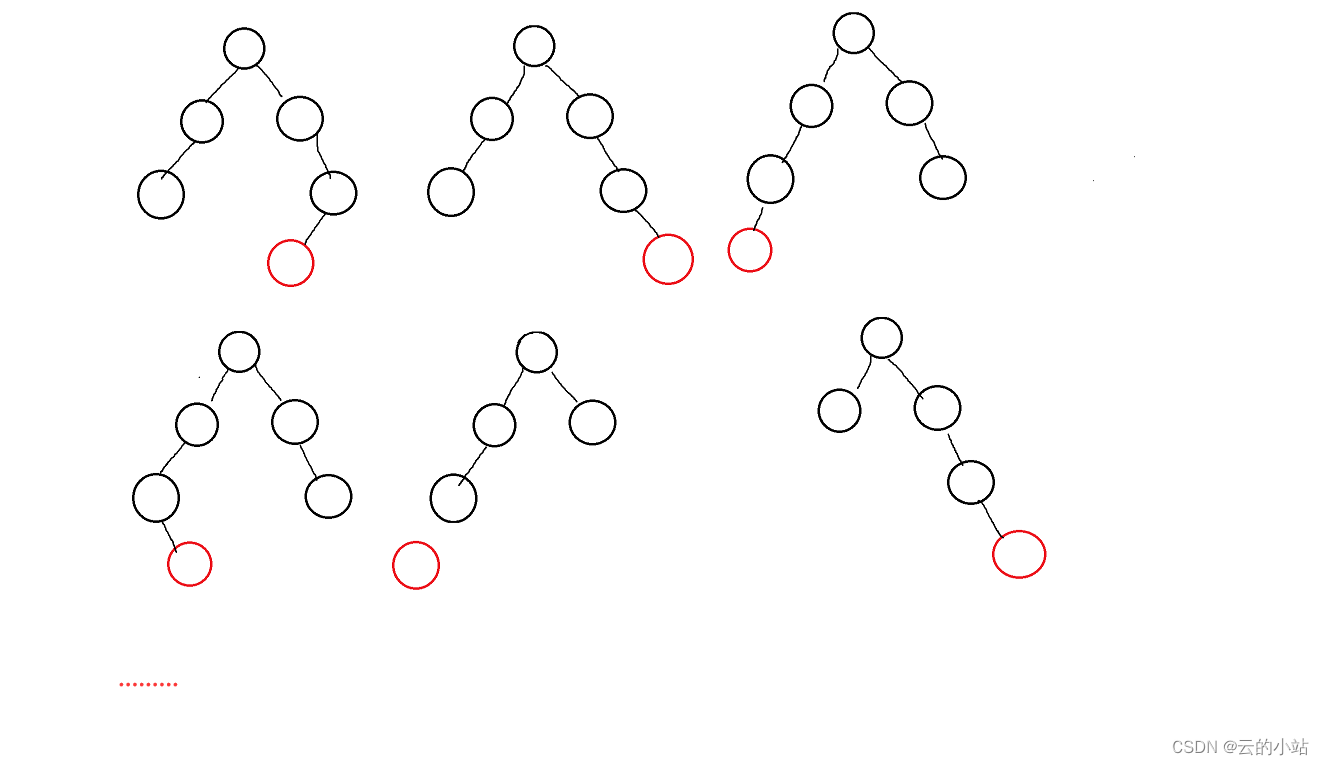
 我们向大佬学习，得出4个旋转大规律：

1. 新节点插入较高左子树的左侧---左左：右单旋

h为子树高度。

当cur->bf==-1&&parent==-2是发生右单旋。

左左的意思是插入数据在parent的左子树的左子树上。

右单旋：以60结点为中心，向右旋转AVL树，允许h=0；

观察图像，我们发现就是改变链接关系，

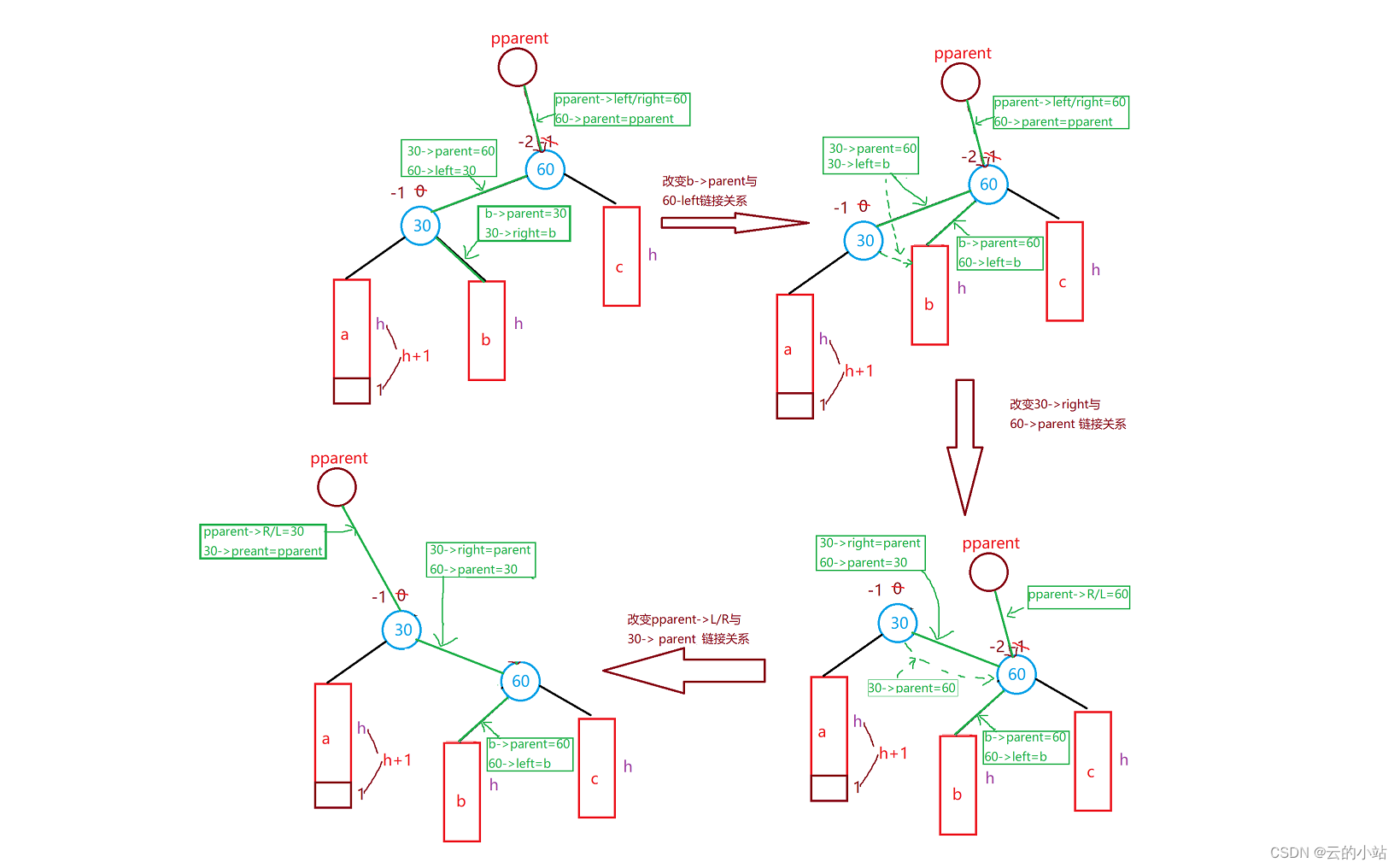
 这里有2个小细节点，

  1. b允许为空，所以b的parent操作前需要判断b是否为nullptr
  2. 如果60就是整棵AVL树的根就需要改变root指向30，并且将30的parent置空

在旋转结束以后将cur与parent结点的bf置为0

完整代码：

		void RotateR(Node* parent)
		{
			Node* subL = parent->_right;
			Node* subLR = subL->_right;

			parent->_left = subLR;
			if (subLR)
			{
				subLR->_parent = parent;
			}
			Node* pparent = parent->_parent;

			parent->_parent = subL;
			subL->_right = parent;
			if (_root == parent)
			{
				_root = subL;
				subL->_parent == nullptr;
			}
			else
			{
				if (pparent->_left == parent)
				{
					pparent->_left = subL;
				}
				else
				{
					pparent->_right = subL;
				}
				subL->_parent = pparent;
			}
			subL->_bf = 0;
			parent->_bf = 0;
		}

2.新节点插入较高右子树的右侧---右右：左单旋

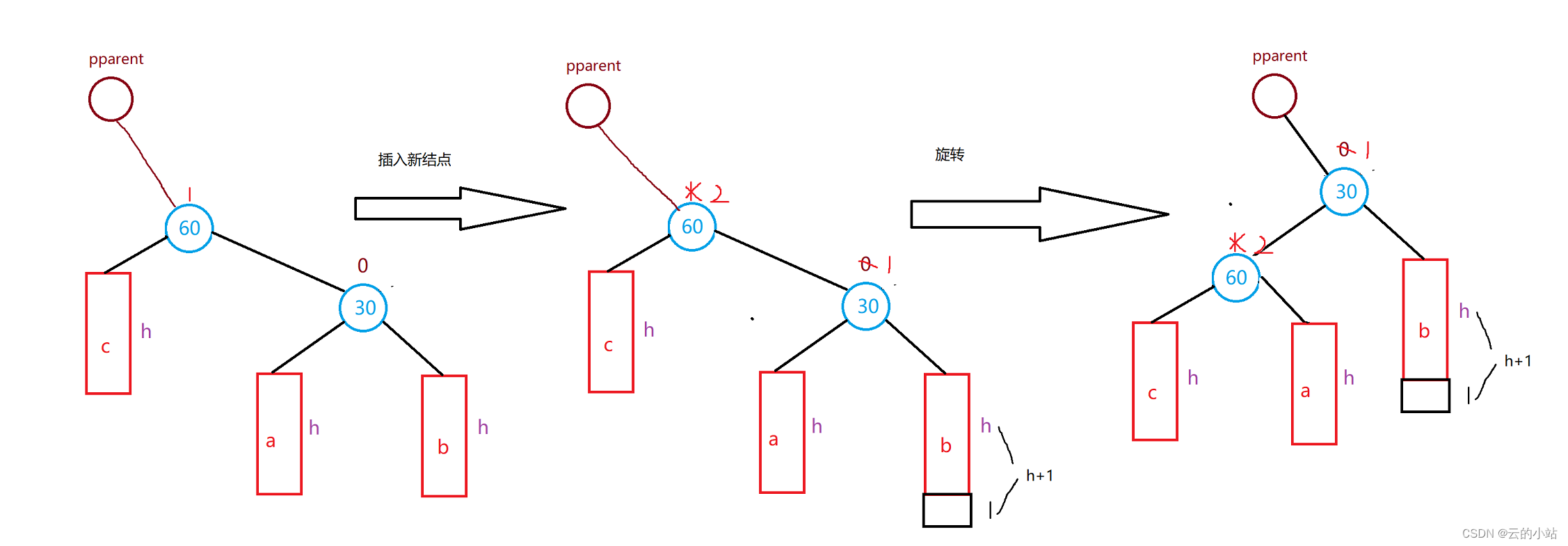
原理与右单旋一样。

查看代码

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	if (subRL)
	{
		subRL->_parent = parent;
	}
	Node* pparent = parent->_parent;

	parent->_parent = subR;
	subR->_left = parent;
	if (_root == parent)
	{
		_root = subR;
		subR->_parent == nullptr;
	}
	else
	{
		if (pparent->_left == parent)
		{
			pparent->_left = subR;
		}
		else
		{
			pparent->_right = subR;
		}
		subR->_parent = pparent;
	}
	subR->_bf = 0;
	parent->_bf = 0;
}

新节点插入较高左子树的右侧---左右：先左单旋再右单旋

什么意思呢？就是插入到了parent->left->right子树上

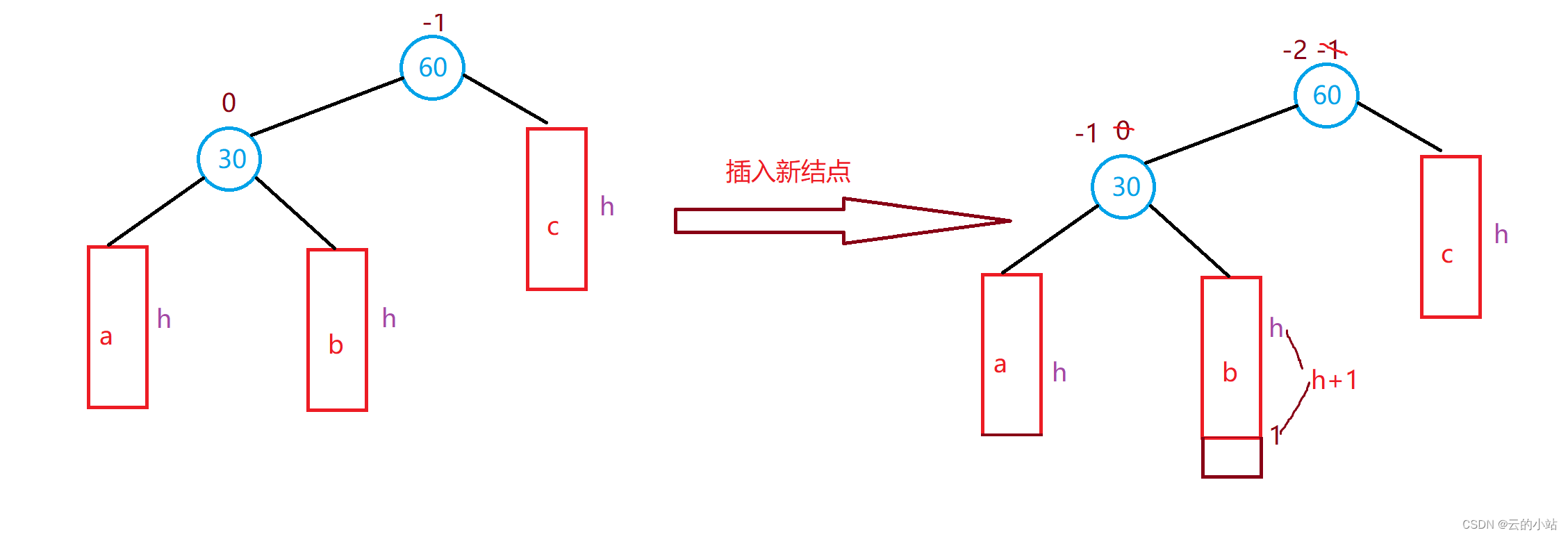
 如果这样的情况只用右单旋。会发生什么呢？

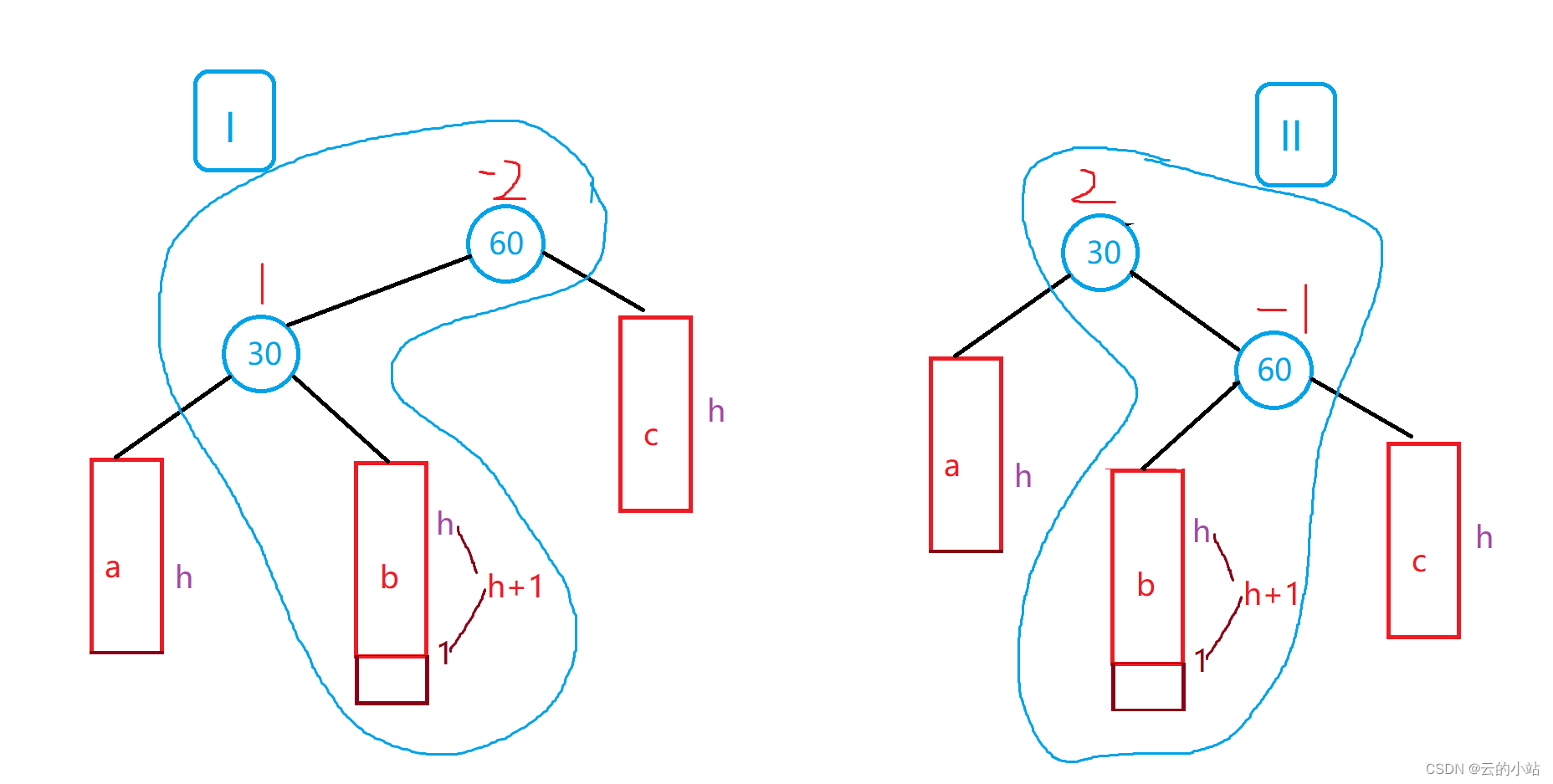
该破坏平衡依旧破坏平衡，用左旋就是I变2一样的。

所以这时候我们需要左右旋一起用。

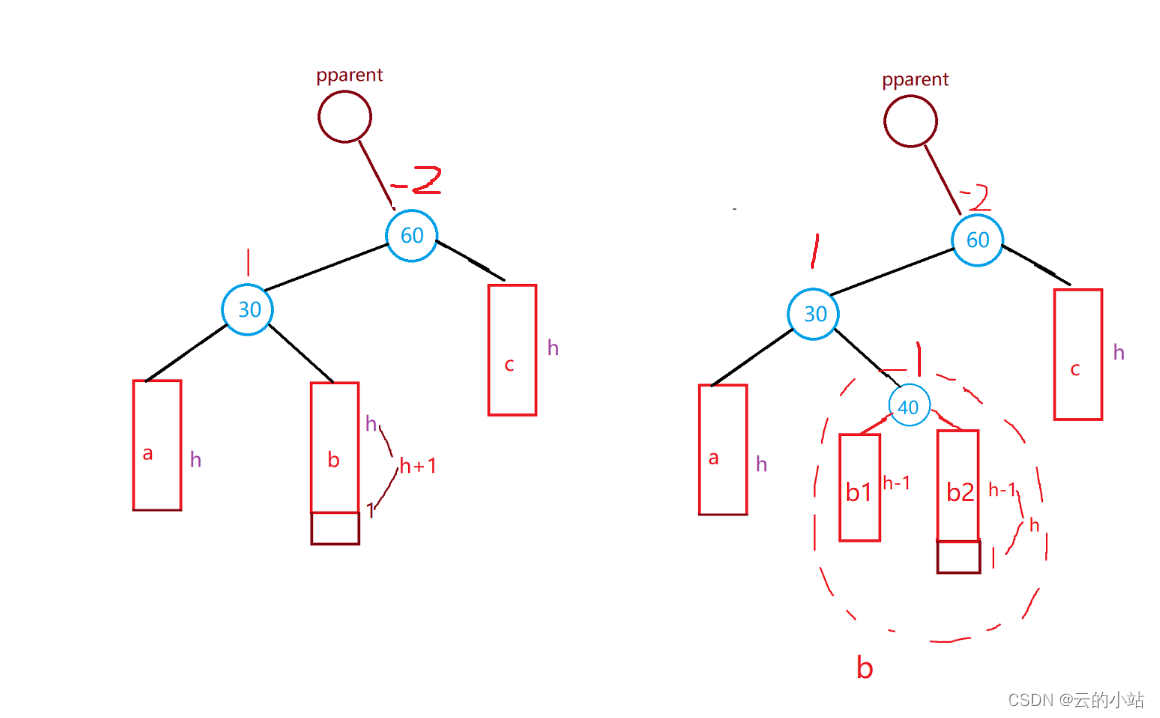
我们将30结点的右子树再一次拆分->40根结点+左右子树。

我们需要先以30结点左旋该子树。

 

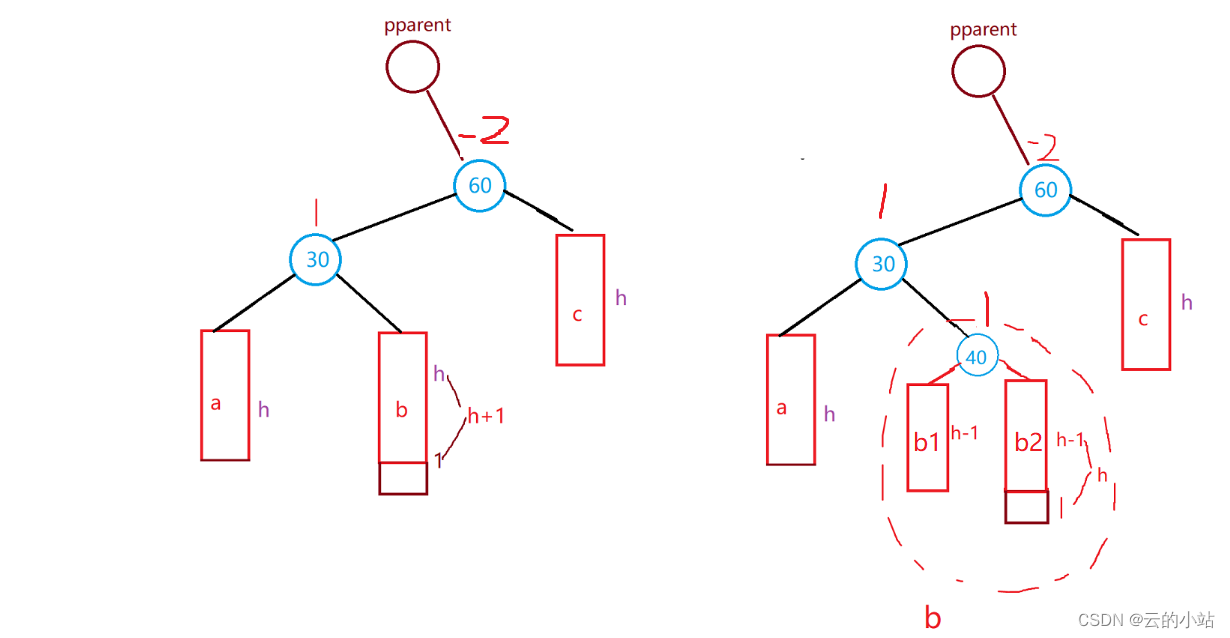
 在根据60结点做右旋旋转，我们把40的左子树看成一个整体

 

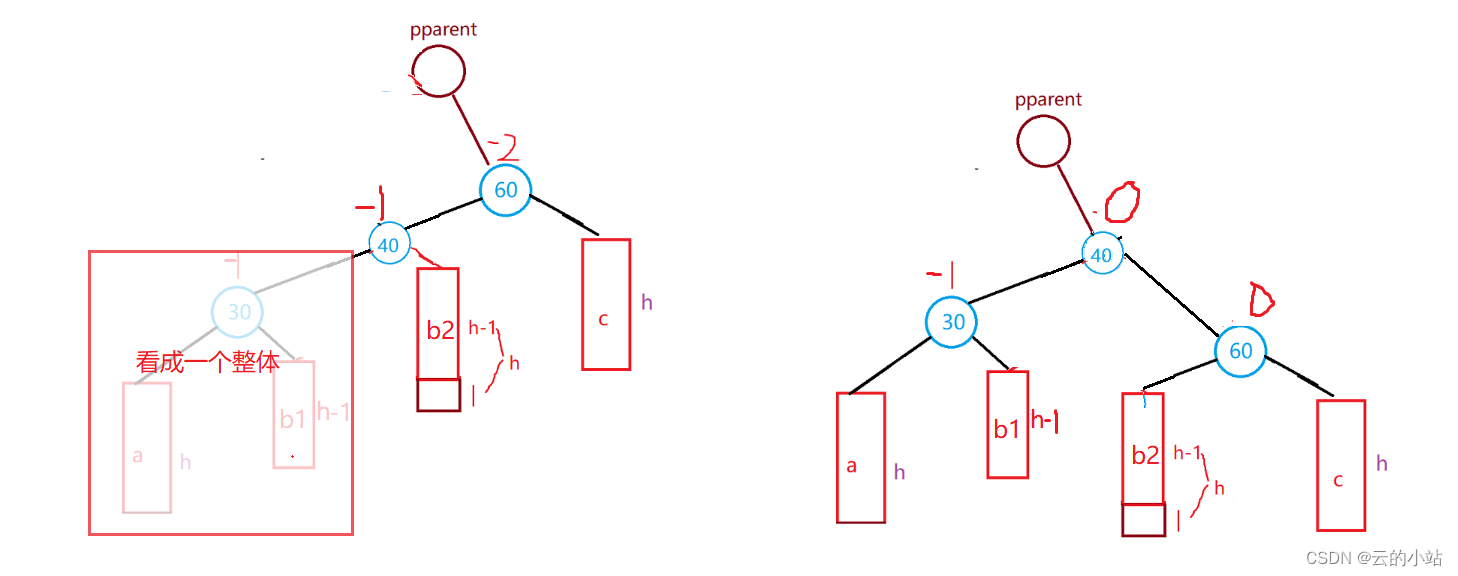
 然后重新定义40、60、30的平衡因子。

这里我们定义平衡因子又有讲究，我们要观察插入后旋转前40结点的平衡因子。

三种情况：

旋转前40->bf==1时，在旋转完毕后30->bf=-1、60->bf=0、40->bf=0；

 

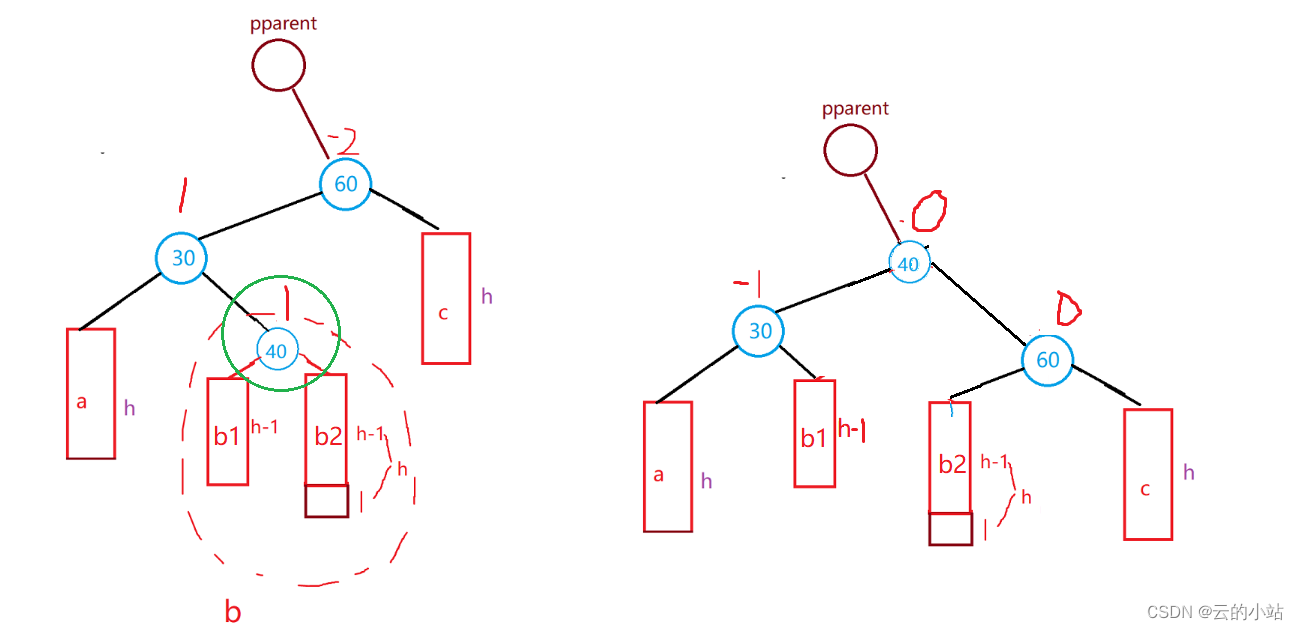
旋转前40->bf==-1时，在旋转完毕后30->bf=0、60->bf=1、40->bf=0；

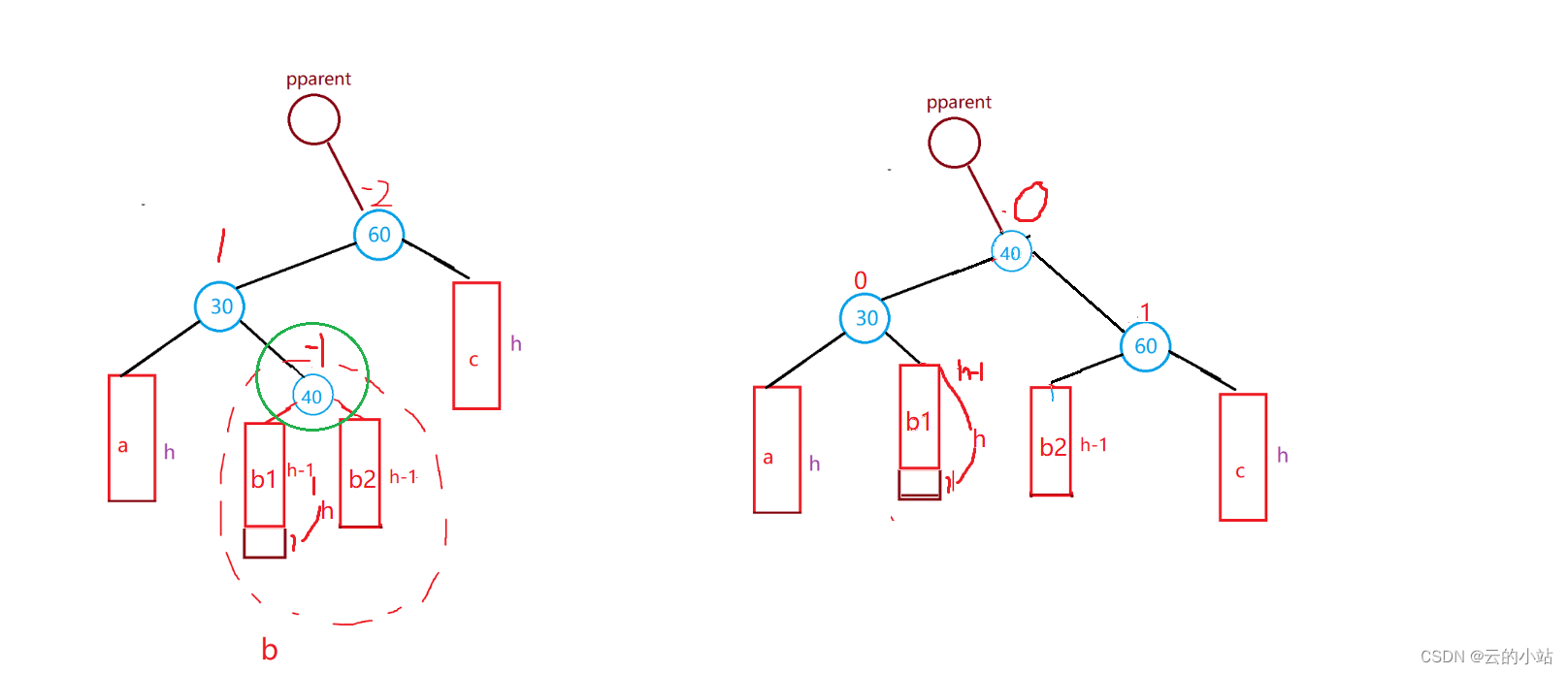
 还有一种特殊的情况40->bf==0;30->bf=0、60->bf=0、40->bf=0；

左右旋代码代码：

        void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int bf = subLR->_bf;
			RotateL(subL);
			RotateR(parent);
			subLR->_bf = 0;
			if (bf == 1)
			{
				parent->_bf = 0;
				subL->_bf = -1;
			}
			else if (bf==-1)
			{
				parent->_bf = 1;
				subL->_bf = 0;
			}
			else if (bf == 0)
			{
				parent->_bf = 0;
				subL->_bf = 0;
			}
			else
			{
				assert(false);
			}
		}

 新节点插入较高右子树的左侧---右左：先右单旋再左单旋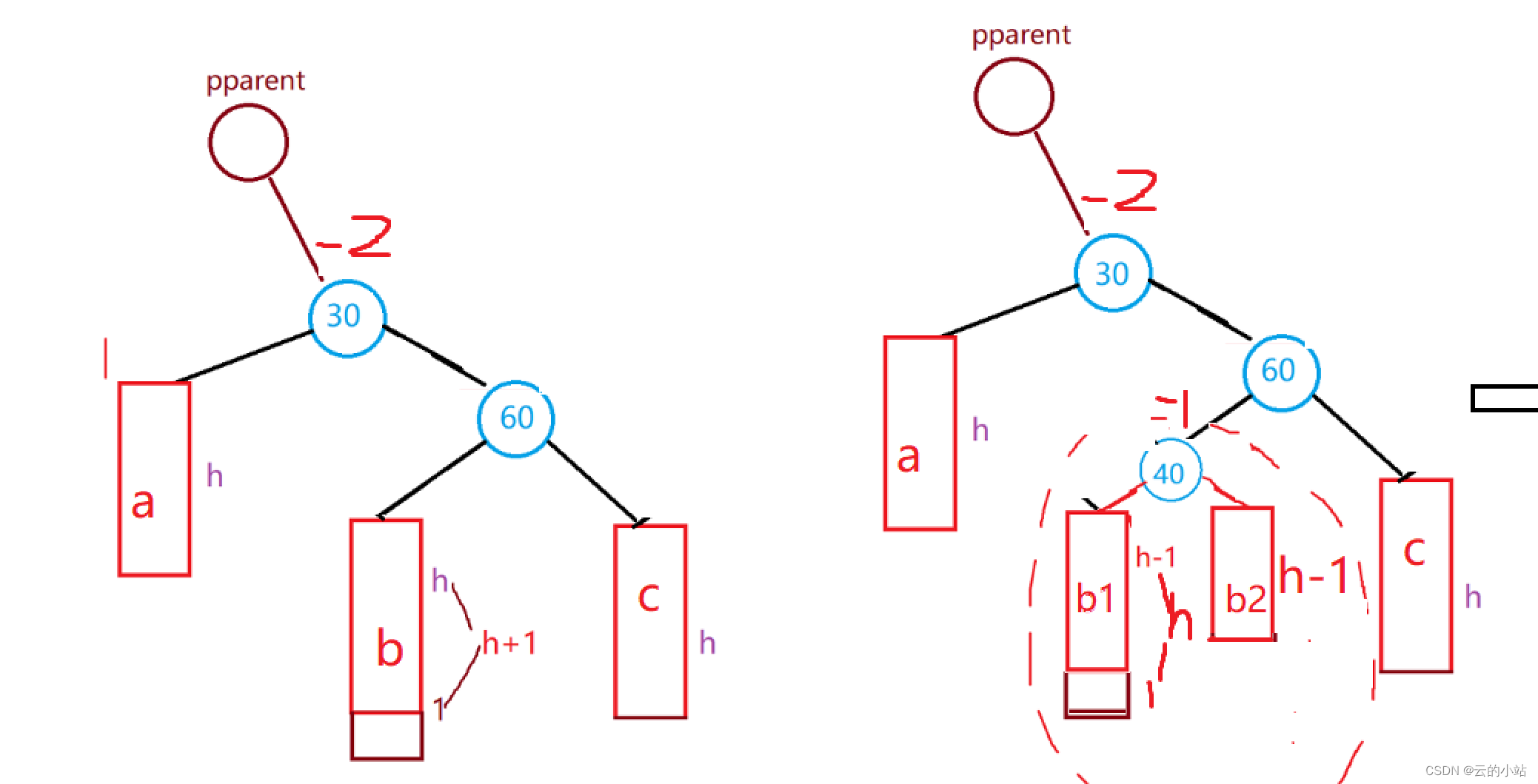

 

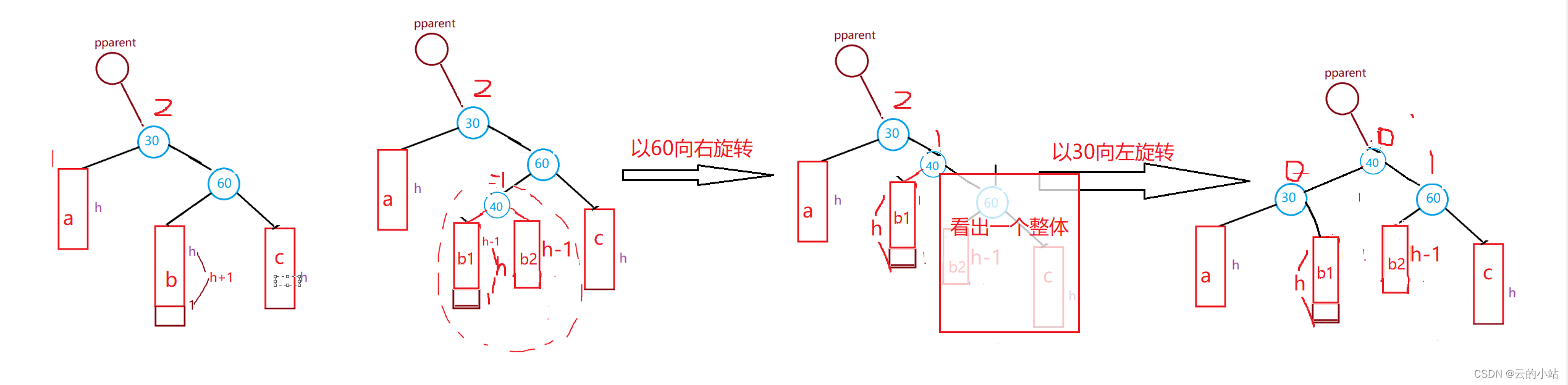
 重新赋值bf与左右：先左单旋再右单旋规则一样

旋转前40->bf==-1时，在旋转完毕后30->bf=0、30->bf=1、40->bf=0；

 

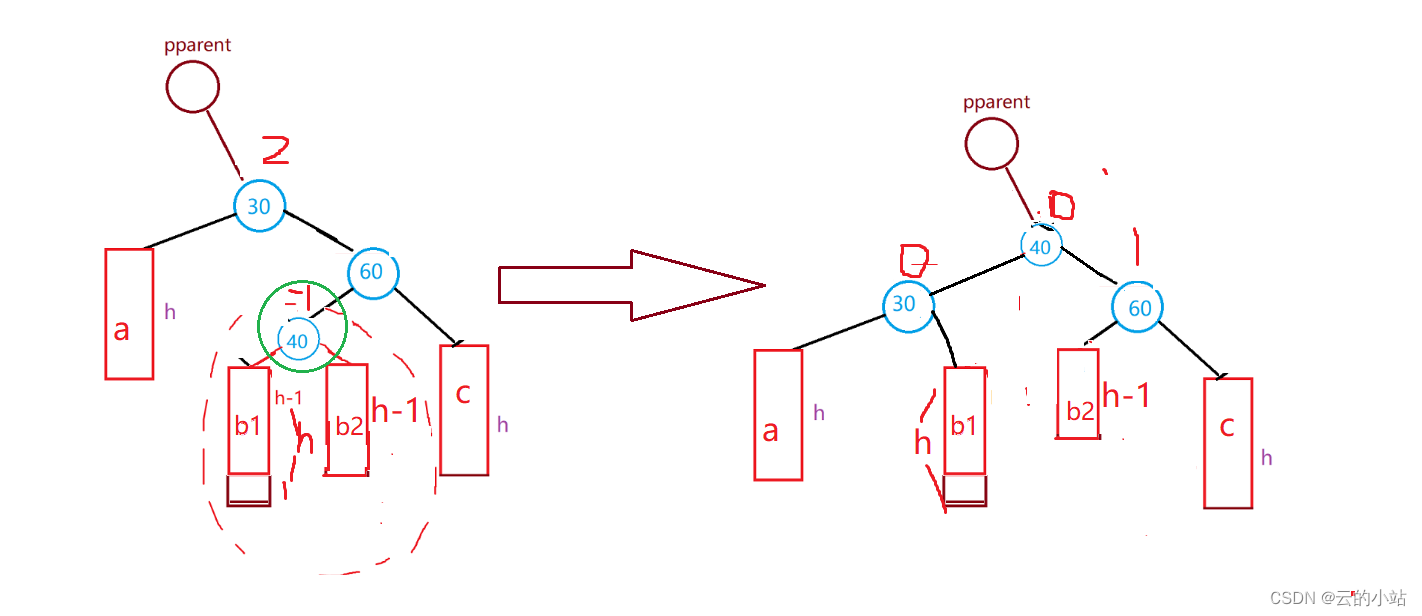
 旋转前40->bf==1时，在旋转完毕后30->bf=-1、30->bf=0、40->bf=0；

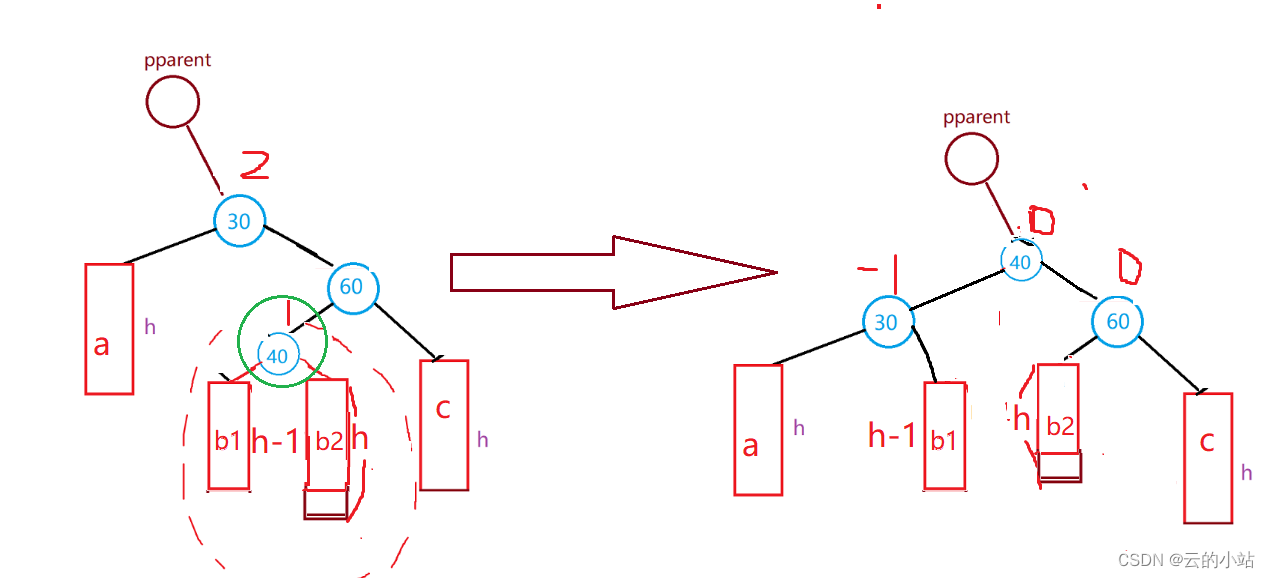
  旋转前40->bf==0时，在旋转完毕后30->bf=-1、30->bf=0、40->bf=0

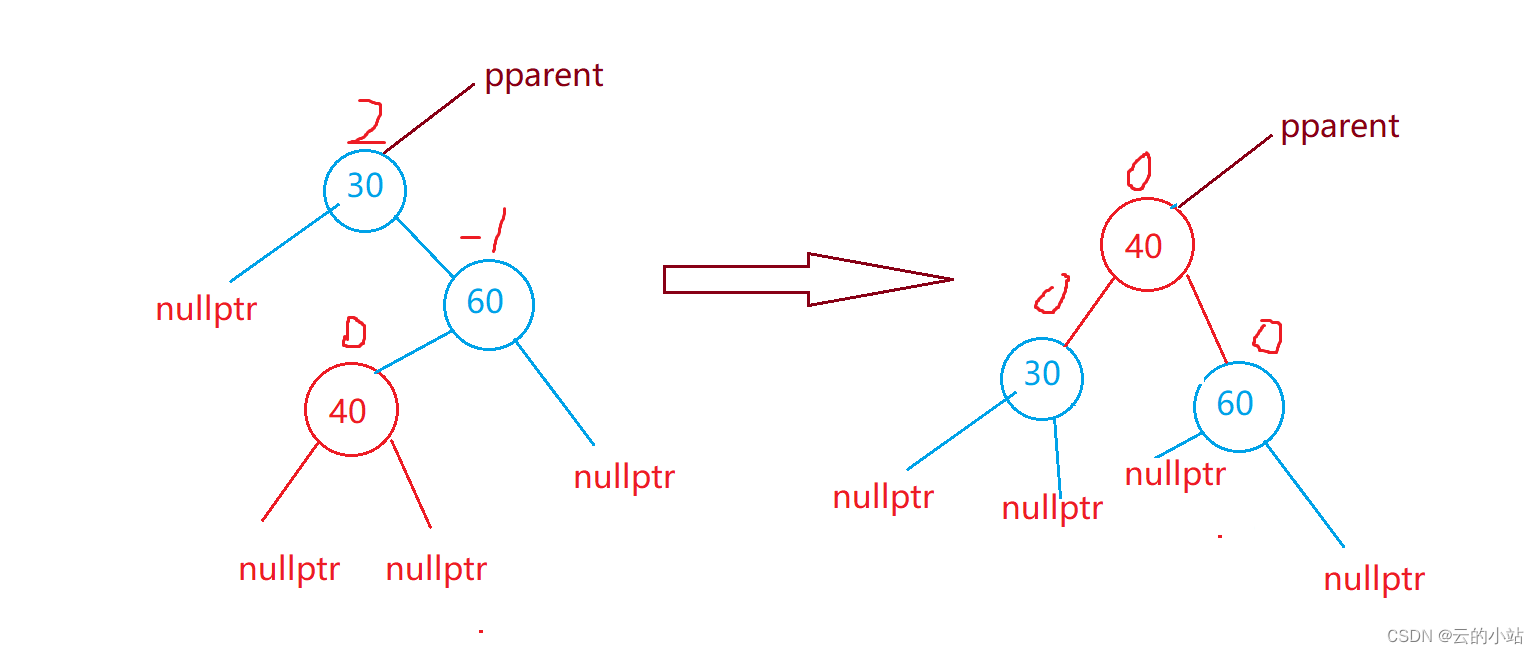
右左旋代码：

		void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL=subR->_left;
			int bf = subRL->_bf;
			RotateR(subR);
			RotateL(parent);
			subRL->_bf = 0;
			if (bf == 1)
			{
				parent = -1;
				subR = 0;
			}
			else if(bf==-1)
			{
				parent = 0;
				subR = 1;
			}
			else if (bf == 0)
			{
				parent = 0;
				subR = 0;
			}
			else
			{
				assert(0);
			}
		}

 AVLinsert完整代码：

template<class K, class V>
	struct AVLTree
	{
		typedef AVLTreeNode<K, V> Node;
	public:
		bool Insert(const pair<K, V>& kv)
		{
			if (_root == nullptr)
			{
				_root = new Node(kv);
			}
			else
			{
				Node* parent = nullptr;
				Node* cur = _root;
				while (cur)
				{
					parent = cur;
					if (cur->_kv.first > kv.first)
					{
						cur = cur->_left;
					}
					else if (cur->_kv.first < kv.first)
					{
						cur = cur->_right;
					}
					else
					{
						return false;
					}
				}
				cur = new Node(kv);
				if (parent->_kv.first <cur->_kv.first)
				{
					parent->_right = cur;
				}
				else
				{
					parent->_left = cur;
				}
				cur->_parent = parent;
				while (parent)
				{

					if (parent->_right == cur)
					{
						++parent->_bf;
					}
					else 
					{
						--parent->_bf;
					}
					if (parent->_bf == 0)
					{
						break;
					}
					else if (abs(parent->_bf) == 1)
					{
						cur = parent;
						parent = parent->_parent;
					}
					else if (abs(parent->_bf) == 2)
					{
						if (parent->_bf == 2 && cur->_bf == 1)
						{
							RotateL(parent);
						}
						else if (parent->_bf == -2 && cur->_bf == -1)
						{
							RotateR(parent);
						}
						else if (parent->_bf == -2 && cur->_bf == 1)
						{
							RotateLR(parent);
						}
						else if (parent->_bf == 2 && cur->_bf == -1)
						{
							RotateRL(parent);
						}
						break;
					}
					else
					{
						std::cout << "AVL fail\n";
						assert(false);
					}
				}
				
				return true;
			}
		}
	private:
		void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int bf = subLR->_bf;
			RotateL(subL);
			RotateR(parent);
			subLR->_bf = 0;
			if (bf == 1)
			{
				parent->_bf = 0;
				subL->_bf = -1;
			}
			else if (bf==-1)
			{
				parent->_bf = 1;
				subL->_bf = 0;
			}
			else if (bf == 0)
			{
				parent->_bf = 0;
				subL->_bf = 0;
			}
			else
			{
                printf("bf is fail!!\n");
				assert(false);
			}
		}

		void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL=subR->_left;
			int bf = subRL->_bf;
			RotateR(subR);
			RotateL(parent);
			subRL->_bf = 0;
			if (bf == 1)
			{
				parent = -1;
				subR = 0;
			}
			else if(bf==-1)
			{
				parent = 0;
				subR = 1;
			}
			else if (bf == 0)
			{
				parent = 0;
				subR = 0;
			}
			else
			{
                printf("bf is fail!!\n");
				assert(false);
			}

		}
		void RotateL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			
			parent->_right = subRL;
			if (subRL) 
			{
				subRL->_parent = parent;
			}
			Node* pparent = parent->_parent;

			parent->_parent = subR;
			subR->_left = parent;
			if (_root == parent)
			{
				_root = subR;
				subR->_parent == nullptr;
			}
			else
			{
				if (pparent->_left == parent)
				{
					pparent->_left = subR;
				}
				else
				{
					pparent->_right = subR;
				}
				subR->_parent = pparent;
			}
			subR->_bf = 0;
			parent->_bf = 0;
		}

		void RotateR(Node* parent)
		{
			Node* subL = parent->_right;
			Node* subLR = subL->_right;

			parent->_left = subLR;
			if (subLR)
			{
				subLR->_parent = parent;
			}
			Node* pparent = parent->_parent;

			parent->_parent = subL;
			subL->_right = parent;
			if (_root == parent)
			{
				_root = subL;
				subL->_parent == nullptr;
			}
			else
			{
				if (pparent->_left == parent)
				{
					pparent->_left = subL;
				}
				else
				{
					pparent->_right = subL;
				}
				subL->_parent = pparent;
			}
			subL->_bf = 0;
			parent->_bf = 0;
		}

		Node* _root;
	};
}

 谢谢！！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/664747.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JVM知识点梳理

JVM知识点梳理

什么是JVM&#xff1f; JVM是java虚拟机的缩写 &#xff0c;也是java程式可以实现跨平台的关键。 JVM部分需要知道什么东西&#xff1f; JVM的结构和功能、参数配置、GC回收机制、GC回收器极其优缺点。 JVM结构&#xff08;栈&#xff0c;程序计数器&#xff0c;方法区&#xf…
阅读更多...
0009-TIPS-SLAB入门与观察

0009-TIPS-SLAB入门与观察

极简&#xff0c;但是能快速上手 slub算法 这篇文章简洁直观&#xff0c;推荐 linux 内核 内存管理 slub算法 &#xff08;一&#xff09; 原理 感受slub堆漏洞 需要下载 https://github.com/De4dCr0w/green-dill &#xff0c;使用其中的测试程序做实验 UAF 如果看完上面链…
阅读更多...
F407/103启动文件and启动过程

F407/103启动文件and启动过程

STM32 启动文件简介 STM32 启动文件由 ST 官方提供&#xff0c;在官方的固件包里。 startup_stm32f40_41xxx.s 启动文件由汇编编写&#xff0c;是系统上电复位后第一个执行的程序。 启动文件主要做了以下工作&#xff1a; 1 、初始化堆栈指针 SP _initial_sp 2 、初始…
阅读更多...
SSM面试题

SSM面试题

文章目录 一、Spring1.1 配置一个bean的方式?注解/xml1.2 spring 自动装配 bean 有哪些方式?1.3 spring 常用的注入方式有哪些?1.4 Component和Bean的区别?1.5 spring 事务实现方式有哪些?1.6 spring事务的传播机制?1.7 spring 的事务隔离? 二、SpringMVC2.1 SpringlIvc…
阅读更多...
阿里云在国内市场占有率怎么样？

阿里云在国内市场占有率怎么样？

阿里云在国内市场占有率怎么样&#xff1f; 　　阿里云在国内市场占有率分析 　　随着互联网的飞速发展&#xff0c;越来越多的企业和个人开始利用云计算服务来满足各种业务需求。作为中国领先的云服务提供商&#xff0c;阿里云自成立以来就受到了广泛关注。本文旨在分析阿里云…
阅读更多...
cmake入门(2)

cmake入门(2)

cmake 教程2 demo cmake_minimum_required(VERSION 3.10) project(Tutorial)set(CMAKE_CXX_STANDARD 11) set(CMAKE_CXX_STANDARD_REQUIRED True)add_executable(Tutorial tutorial.cxx)基础 cmake_minimum_required cmake的版本要求 project 项目的名字&#xff0c;同时会生…
阅读更多...
ad18学习笔记五：统计焊盘数量(board information)

ad18学习笔记五：统计焊盘数量(board information)

AD18之后&#xff0c;Altium Designer改动比较大。下面将介绍AD19如何统计焊盘(PAD数量)与SMT贴片数量与插件数量 1&#xff1a; PCB 空白处 -> F11 -> Properties 选项卡 -> Board Information -> Pads 2&#xff1a; Pads 包括 通孔焊盘和贴片焊盘 Vias 包括过孔…
阅读更多...
22.小波神经网络时间序列预测交通流量（附matlab程序）

22.小波神经网络时间序列预测交通流量（附matlab程序）

1.简述 学习目标&#xff1a;小波神经网络时间序列预测交通流量 WNN&#xff08;小波神经网络&#xff09;&#xff1a;是在误差反传神经网络拓扑结构的基础上发展而来的网络&#xff0c;与神经网络的结构具有一定的相似&#xff0e;在小波神经网络中&#xff0c;当整体信号…
阅读更多...
第十三章 csv模块

第十三章 csv模块

1. csv模块介绍 介绍csv 模块前&#xff0c;需要先了解csv 文件&#xff08;.csv 文件格式&#xff09;&#xff0c;csv 文件中的每行代表电子表格中的一行&#xff0c;并用逗号分隔该行中的单元格。 csv 文件可以使用记事本打开&#xff0c;可以使用Excel 另存为.csv 文件格…
阅读更多...
docker内访问tdengine服务

docker内访问tdengine服务

踩坑记 springboot项目使用docker部署。由于tdengine原生连接方式需要安装客户端&#xff0c;第一想法是宿主机装好客户端&#xff0c;然后映射驱动到容器内部&#xff0c;网上找的教程也基本是这种思路。尝试了一天失败了。 错误1:libjemalloc.so.2 file: No such file or d…
阅读更多...
docker安装下载tomcat一站式搞定并设置挂载卷

docker安装下载tomcat一站式搞定并设置挂载卷

阿丹&#xff1a; 之前在使用nginx部署搭建vue项目的时候没有出docker配置nginx的配置文档&#xff08;因为之前使用的是腾讯云现成的nginx服务器&#xff09;&#xff0c;今天配置安装一下tomcat和nginx在docker里面的安装。 在docker中安装配置tomcat 操作解读&#xff1a;…
阅读更多...
服务器中间件

服务器中间件

文章目录 一、tomcat二、 nginx2.1 代理问题2.2 负载均衡问题2.3 资源优化2.4 Nginx处理2.5 Nginx的特点&#xff1a;2.6 Nginx的安装2.7 Nginx的配置文件2.8 Nginx的反向代理2.9 反向代理&#xff1a;2.10 基于Nginx实现反向代理2.11 关于Nginx的location路径映射2.12 负载均衡…
阅读更多...
【实战项目】利用mmdetection识别卫星遥感影像上的电线杆塔

【实战项目】利用mmdetection识别卫星遥感影像上的电线杆塔

前言 这次项目算是对openmmlab AI实战营第二期的一个实验证明&#xff0c;虽然这几天学习的比较粗糙&#xff0c;但也算是入门了mmdetection。 这个工具就像python一样&#xff0c;openmmlab已经将入门门槛做的很低了&#xff0c;但如果想精进、熟练甚至做真正的调参侠&#xf…
阅读更多...
小白到运维工程师自学之路 第三十九集 (LVS架构)

小白到运维工程师自学之路 第三十九集 (LVS架构)

一、概述 1、lvs LVS是Linux Virtual Server的缩写&#xff0c;是一种基于Linux内核的高性能、高可用性的 负载均衡软件。它可以将多台服务器组成一个虚拟的服务器集群&#xff0c;通过负载均衡算法将 客户端请求分发到不同的服务器上&#xff0c;从而提高系统的可用性和性能…
阅读更多...
【MQTT 5.0】协议 ——发布订阅模式、Qos、keepalive、连接认证、消息结构

【MQTT 5.0】协议 ——发布订阅模式、Qos、keepalive、连接认证、消息结构

一、前言1.1 MQTT 协议概述1.2 MQTT规范 二、MQTT 协议基本概念2.1 发布/订阅模式2.11 MQTT 发布/订阅模式2.12 MQTT 发布/订阅中的消息路由2.13 MQTT 与 HTTP 对比2.14 MQTT 与消息队列 2.2 服务质量&#xff1a;QoS2.21 QoS 0 最多分发一次2.22 QoS1 至少分发一次2.23 QoS 2 …
阅读更多...
一款可以支持SNMP协议的网络型温湿度变送器资料

一款可以支持SNMP协议的网络型温湿度变送器资料

简单网络管理协议&#xff08;SNMP&#xff09;&#xff0c;由一组网络管理的标准组成&#xff0c;包含一个应用层协议&#xff08;application layer protocol&#xff09;、数据库模型&#xff08;database schema&#xff09;和一组资料物件。该协议能够支持网络管理系统&am…
阅读更多...
generator和promise和async的异同

generator和promise和async的异同

一、generator(生成器)是ES6标准引入的新数据类型,他和promise一样都是异步事件的解决方案 //generator函数生成斐波那契// generator(生成器)是ES6标准引入的新数据类型,async就是 Generator 函数的语法糖//本质&#xff1a;用来处理异步事件的对象/包含异步操作的容器functio…
阅读更多...
Rust语言从入门到入坑——(4)Rust语法（中）

Rust语言从入门到入坑——(4)Rust语法（中）

文章目录 0 引入1、函数1.1、函数参数1.2、函数体1.3、函数返回值 2、条件语句3、循环3.1 、while3.2 、for3.3 、loop循环 4、总结 0 引入 在这里我们需要介绍Rust语法&#xff0c;一共分三部分&#xff0c;第二部分主要是一些如函数&#xff0c;编程中的循环等语法的介绍&am…
阅读更多...
小白到运维工程师自学之路 第三十九集 （HAproxy 负载均衡）

小白到运维工程师自学之路 第三十九集 （HAproxy 负载均衡）

一、概述 HAProxy是一款高性能的负载均衡软件&#xff0c;可以将来自客户端的请求分发到多个服务器上&#xff0c;以提高系统的可用性和性能。HAProxy支持多种负载均衡算法&#xff0c;包括轮询、加权轮询、最少连接数等。同时&#xff0c;HAProxy还支持会话保持、健康检查、SS…
阅读更多...
redis和mysql

redis和mysql

文章目录 一、redis1.1 redis的数据结构都有哪些&#xff1f;1.2 持久化方式有哪些&#xff1f;1.3 怎么保证缓存和数据库数据的一致性?1.4 redis缓存是什么意思&#xff1f; 二、数据库2.1 基本数据类型2.2 MySQL 的内连接、左连接、右连接有什么区别?2.3 MySQL 问题排查都有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023