在计算流线，拉格朗日拟序结构等流场后处理时，我们常常需要计算无质量的粒子在流场中迁移时的轨迹，无质量意味着粒子的速度为流场当地的速度。此时，求解粒子的位移这个问题是一个非常简单的常微分方程问题。
$$\begin{gathered} 假设流场中存在i个粒子，那么对于每个粒子有 \\ {v}_i=x_i \\ 初始条件为：x_i(t_0) \end{gathered}$$
1、欧拉向前差分
欧拉向前差分是最简单的方法，其主要步骤为：
$$\begin{gathered} {x}_i^{t+dt}=x_i+v_i^t\ast dt \\ {v}_i^t为t时刻在x_i处的流场速度 \end{gathered}$$
显然，该方法的精度取决于时间步长，时间步长越大，误差越大。
该方法需要注意几个事项：
（1）流场插值处理
我们实现知道的流场数据是时间和空间离散的，对于任意一个时刻，我们只知道空间离散点处的流场速度，加入粒子的位置恰好不在这些点上，我们就需要通过插值得到其速度。
matlab提供了这样的插值函数，interp2()。
假设我们现在已知流场的空间离散点矩阵x_f；y_f以及速度U，V;
我们想通过插值获得，ftle_x,ftle_y处粒子的速度ux,uy

ux = interp2(x_f,y_f,U,ftle_x,ftle_y,'linear');
uy = interp2(x_f,y_f,V,ftle_x,ftle_y,'linear');
%%上面的代码中ftle_x,ftle_y可以是矩阵形式，这样得到的速度ux,uy也是矩阵    

那么接下来粒子迁移就十分简单了

for t = f_time:dt:(T+f_time)
    %获取t时刻的速度数据
    U = reshape(vel(1:Nx*Ny,t),Ny,Nx);
    V = reshape(vel(Nx*Ny+1:end,t),Ny,Nx);
    %%计算粒子迁移t-->t+dt
    ux = interp2(x_f,y_f,U,ftle_x,ftle_y,'linear');
    uy = interp2(x_f,y_f,V,ftle_x,ftle_y,'linear');

    X = ftle_x + dt*tstep*ux;
    Y = ftle_y + dt*tstep*uy;
    ftle_x=X;
    ftle_y=Y;
end

另外，好像对于这个问题不能用梯型方法？梯型方法的步骤如下：
$$y_{n+1}=y_n+\frac{h}{2}\left(f\right(x_n,y_n)+f(x_{n+1},y_{n+1})$$
主要问题在于我没法知道下一步粒子在哪，即这里的x(n+1),y(n+1)，因为我就是在求这个东西？
暂时没想明白怎么用梯型方法。
2、龙格-库塔法
这个就比较玄学了，这个我也没弄清原理，只是知道matlab里有这个函数可以用，并且还不错。
由于龙格-库塔法需要两个时间步中间的时刻，我们不仅需要空间插值，还需要时间插值。
插值的方法也很简单，matlab提供了相应的函数
（1）首先我们需要获得粒子的时间，空间离散结果

for k = 1:size(vel,2)
    XX(:,:,k) = X0;
    YY(:,:,k) = Y0;%%这里是给定了每个时刻的离散空间位置，我们采用欧拉法求解流场，所以离散点是固定的
    u(:,:,k) = reshape(vel(1:ny*nx,k),[ny nx]);
    v(:,:,k) = reshape(vel(ny*nx+1:end,k),[ny nx]);
    TT(:,:,k) = t(k)*ones(ny,nx);%%这里存储着每个粒子的时间信息，因为全场内每个粒子的时间是相同的，所以用了ones()函数
end

（2）对其进行转置（该步骤不是必要的）

%% 该部分的操作相当于对一个三维矩阵的前两维进行转置
P = [2 1 3];    
Xprime = permute(XX,P);
Yprime = permute(YY,P);
Tprime = permute(TT,P);
Uprime = permute(u,P);
Vprime = permute(v,P);

（3）时空间插值

u_interp = griddedInterpolant(Xprime,Yprime,Tprime,Uprime,'linear');
v_interp = griddedInterpolant(Xprime,Yprime,Tprime,Vprime,'linear'); 

（4）ode45()函数求解

 [t, X_out] = ode45(@velocity_interp_func,intspan(tspan(k),T),[X0(i,j),Y0(i,j)]);
 %% 这里ode45函数需要输入三个参数
 @velocity_interp_func这是句柄，包含着方程的信息
 intspan(tspan(k),T) 这个是从某个时刻计算到某个时刻
 这里具体含义是从tspan(k)时刻推进到tspan(k)+T时刻
 [X0(i,j),Y0(i,j)]是初始场

根据这个函数就可以计算处初始位置在[X0(i,j),Y0(i,j)]，初始时刻为tspan(k)，经过T时间的运动后，最终的位置X_out。X_out包含了每个时刻对应的粒子位置，t即是这些时刻的时间信息。
但是我们只需要最后一个时刻的信息，因此

X_adv(i,j) = X_out(end,1);
Y_adv(i,j) = X_out(end,2);  

需要注意的是，只是计算单独一个粒子的轨迹，要想计算全场的粒子，需要对其进行遍历，然鹅经过实操发现，这个过程还是很耗时的。
这个方法的具体运行原理我还没有搞明白，因为最简单的梯型法现在还没想清楚，所以仅放在这里。

注意：上面两种方法都是利用离散数据得到粒子迁移的，这里我们通过解析解获得时间间隔为0.1下的0：16s时刻共161个流场数据，流场网格划分为均匀划分，nx =201;ny = 101;
流场设置为double_gyre流场
我们计算的问题是：
流场初始0时刻布置201*101个粒子，计算10s时刻时这些粒子的位置。
3、对照组
为了方便对比上面两种方法的精度，我设置了一组对照组，由于流场设置为double_gyre流场，这个流场是存在解析解的，因此我们可以获得任意时刻，任意位置处的精确速度信息。
通过设置时间步长非常小，并且采用欧拉向前推进，可以将这个方法得到的结果精度提升到很高。
我计算了两种精度的结果1、dt=0.01s，2、dt=0.001s

然后将上面两种方法得到的结果与该方法进行对比，从而得到两种方法的误差范围。
4、实验结果

figure(1)
dx = sigma_x - X_ana;
dy = sigma_y - Y_ana;
e_ds = sqrt(dx.^2+dy.^2);
pcolor(e_ds)
shading interp

figure(2)
dx = X_adv - X_ana;
dy = Y_adv - Y_ana;
o_ds = sqrt(dx.^2+dy.^2);
pcolor(o_ds)
shading interp

欧拉法与dt=0.01解析解对比，后者的时间精度是前者的十倍
结果如下：

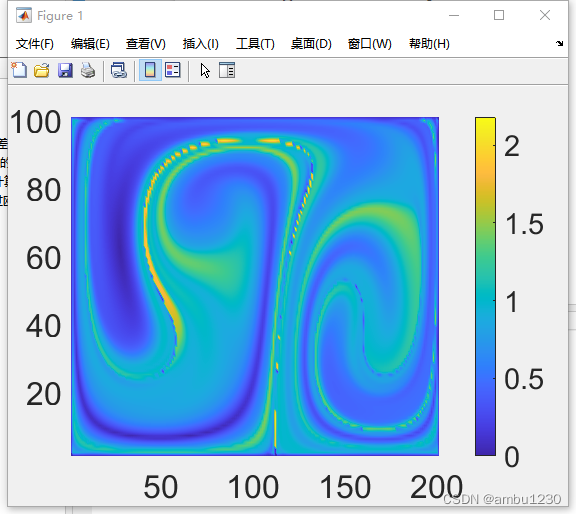
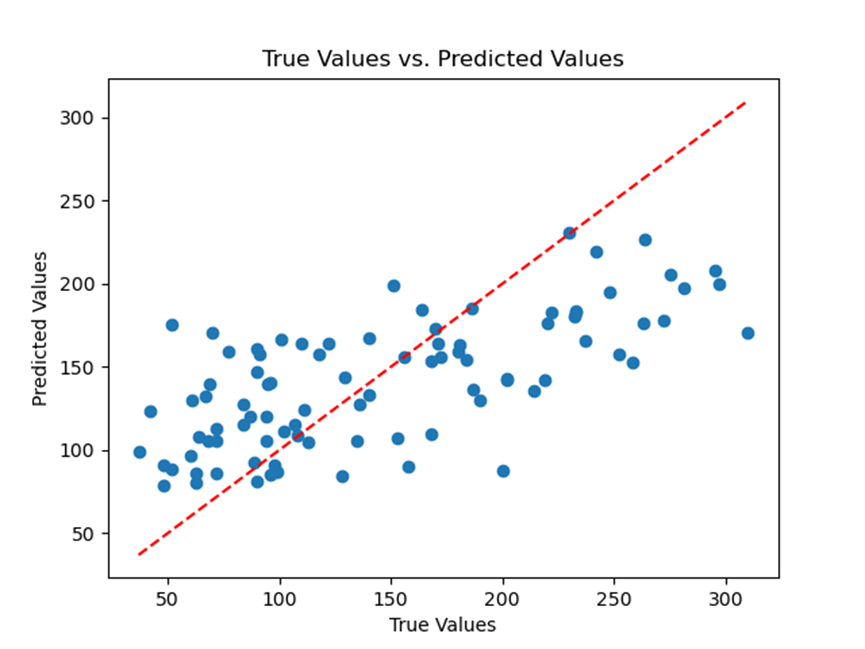
ode45方法结果与dt=0.01解析方法对比
结果如下：

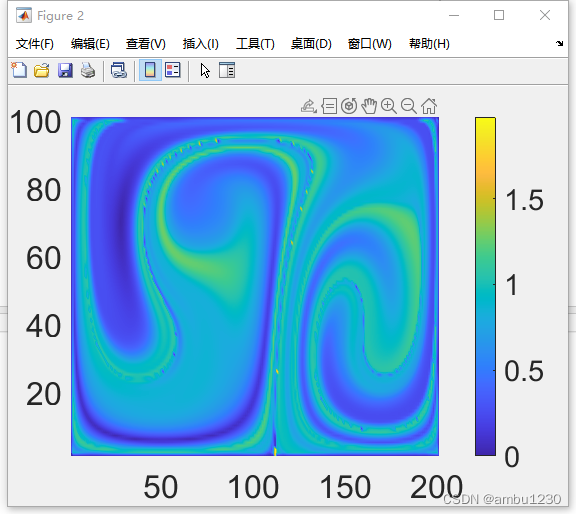
可以看出，欧拉方法的误差要大于ode45方法，但是其实差距不是很大。

我们对误差进行全场平均：
欧拉：0.71
ode45:0.67

误差最大值：
欧拉：2.18
ode45：1.97
这里其实误差还是蛮大的，因为流场范围才是2*1.
还有一个比较神奇的点是，这个误差云图很像ftle图，这是因为ftle图反应了粒子拉伸扭曲的程度，而恰好在这些位置处，误差非常敏感，比较有意思。

最后我们对比了dt=0.01和dt =0.001时解析方法之间的对比结果
其误差云图如下：

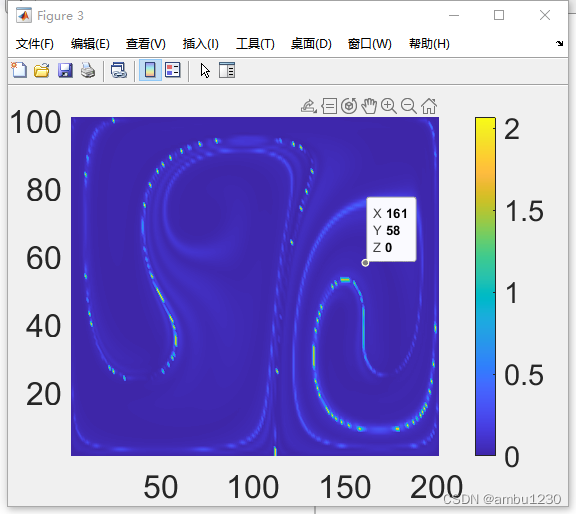
可以看出，dt=0.01时时间精度就已经很高了，与dt=0.001的结果很接近。

补充：总觉得上面的对比还是不够明显，于是又进行了几组测试
dt=0.02;dt=0.05
测试结果，这里仅对比误差平均值：
dt=0.05
欧拉：0.082
ode45：0.091
欧拉方法更接近dt=0.05
dt=0.02
欧拉：0.13
ode45：0.038
ode45方法更接近dt=0.02

可以看出ode45方法其实精度超过了dt=0.05时的解析方法。
对比到此结束，仍然需要指出。虽然平均误差看起来比较大，实际上这些是主要由所谓的FTLE场的脊位置处的粒子贡献的。大多数位置处的粒子误差水平还是比较小的。
下图左为欧拉，右为ode45，蓝色区域的误差还是比较小的。

欧拉方法的误差矩阵：

ode45方法的误差矩阵：