信息量

$$I(x_i)=log\frac{1}{P(x_i)}=-logP(x_i)$$
信息量（self-information），又译为信息本体，由克劳德 · 香农（Claude Shannon）提出，用来衡量单一事件发生时所包含的信息量多寡。任何事件都会承载着一定的信息量，包括已经发生的事件和未发生的事件，只是它们承载的信息量会有所不同。

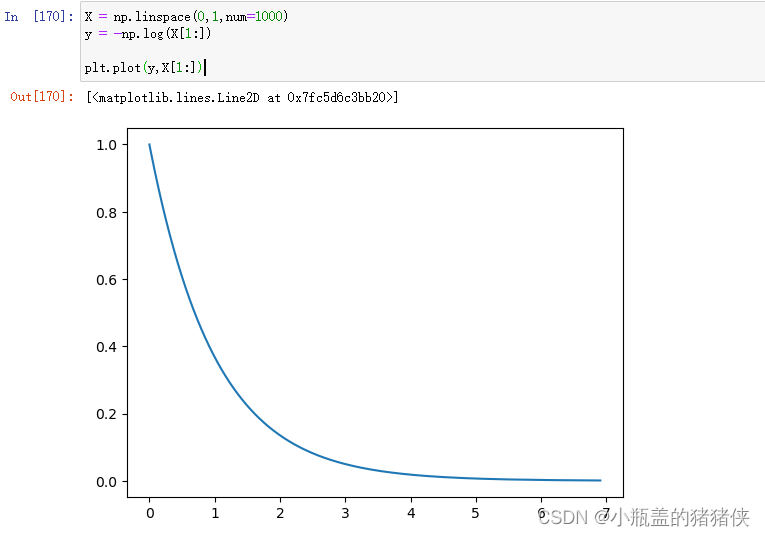
例如对于昨天下雨这个已知事件，因为是已经发生的事件，是既定事实，那么它的信息量就为 0 。对于明天会下雨这个事件，因为未有发生，那么这个事件的信息量就大。我们可以发现信息量是一个与事件发生概率相关的概念。对于一个事件来说，它发生的概率越大，确定性越强，显然它所含有的信息量就越低。一件事情发生的概率越低，不确定性越强，它包含的信息量就越大
相同的$X=x_i,Y=y_i$的联合分布为
$$I(x_i,y_i)=log\frac{1}{p(x_i,y_i)}$$
如果X和Y独立：
$$\begin{gathered} I(x_i,y_i)=log\frac{1}{P(x_i)}+log\frac{1}{P(y_i)} \\ =I(x_i)+I(y_i) \end{gathered}$$

信息量有以下几个性质

• 单调递减性，即发生的概率越小，确定它发生所需要的信息量越大
• $p\to 1$时，$I\to 0$,表示对确定一定会发生事件发生需要的信息量为0
• $p\to 0$时，$I\to \infty$,表示确定不可能事件发生需要的信息量为无穷大。

熵

信息量的数学期望就是信息熵
$$H(X)=-\sum _{i=1}^{n}P(x_i)logP(x_i)$$
熵 (Entropy)，本是热力学中的概念，1948 年，克劳德 · 香农（Claude Shannon）将热力学中的熵的概念引入到信息论中，因此也被称为 信息熵 或香农熵 (Shannon Entropy)，用来衡量信息的不确定度。不准确点说，熵是用来衡量混乱程度的。越混乱，熵越大，代表不确定性越大，要弄清楚情况所需要的信息量越多
举个栗子，一个袋子有 10 个球。如果其中有 5 个红球 5 个白球，这就是混乱的。如果有 9 个红球和 1 个白球，这就不混乱。可以理解为如果各种物品的比例相同，不同物品的概率都很大，那么我想要判断袋子里面有什么东西就比较困难，整体的信息量就很大，就会非常混乱。如果袋子仅有一种物品，那么我判断袋子里的物品就非常容易，这便是不混乱。也即一个集合里面各部分比例越均衡越混乱，各部分越两极分化越不混乱。
那么如何使用数学来衡量混乱程度呢？ 我们显然发现当物品的总数不变的情况下，两种物品数目的乘积越大越混乱，越小越不混乱。那么我们显然就可以用这个相乘的结果来衡量数据混乱程度。既然如此，如果袋子中有多种球，我们可以将他们的概率连乘即可。

信息论之父克劳德·香农，总结出的信息熵的三条性质：

• 单调性，即发生概率越高的事件，其所携带的信息熵越低。极端案例就是“太阳从东方升起”，因为为确定事件，所以不携带任何信息量。从信息论的角度，认为这句话没有消除任何不确定性。
• 非负性，即信息熵不能为负。这个很好理解，因为负的信息，即你得知了某个信息后，却增加了不确定性是不合逻辑的。
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和。

联合熵

与联合自信息相同，我们可以定义两个随机变量 X 和 Y 的联合熵为：
$$\begin{array}{rl}H(X,Y)& =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x)P(y|x))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x))-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(y|x))\\ & =-\sum _{x\in X}P(x)log(P(x))-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(y|x))\\ & =H(X)+H(Y|X)\end{array}$$
在物理意义其度量了一个联合分布的随机系统的不确定度，观察了该随机系统的信息量
当$X=A,Y=B$同时发生且相互独立时，有$P(X=A,Y=B)=P(X=A)\times P(Y=B)$此时信息熵
$$H(X,Y)=H(X)+H(Y)$$

互信息

两个随机变量 X 和 Y 的互信息定义为：
$$\begin{array}{rl}I(X,Y)& =\sum _{x\in X}\sum _{y\in Y}P(x,y)log(\frac{P(x,y)}{P(x)\times P(y)})\\ & =\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y))-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x)\times P(y))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x))-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(y))\\ & -(-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y)))\\ & =-\sum _{x\in X}log(P(x))\sum _{y\in Y}P(x,y)-\sum _{y\in Y}log(P(y))\sum _{x\in X}P(x,y)-(-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y)))\\ & =-\sum _{x\in X}log(P(x))P(x)-\sum _{y\in Y}log(P(y))P(y)-(-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y)))\\ & =H(X)+H(Y)-(X,Y)\\ & =H(Y)-H(Y|X)\\ & =H(X)-H(X|Y)\\ & =H(X,Y)-H(Y|X)-H(X|Y)\end{array}$$
当 X,Y 不相互独立时：
$$I(X,Y)=H(X)+H(Y)-H(X,Y)$$
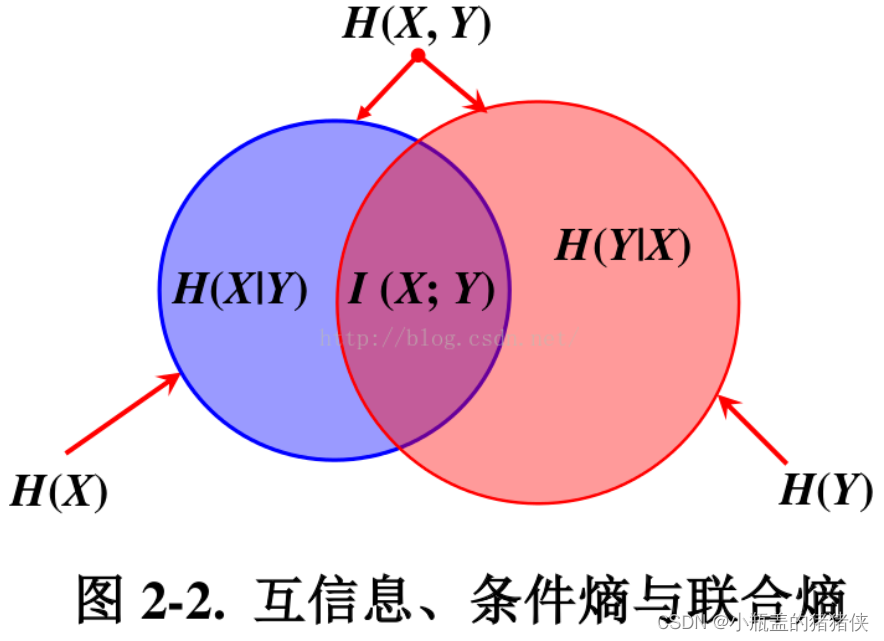
互信息代表一个随机变量包含另一个随机变量信息量的度量。其物理意义表明了两事件单独发生的信息量是有重复的。互信息度量了这种重复的信息量大小。在一个点到点通信系统中，发送端信号为 X ，通过信道后，接收端接收到的信号为 Y ，那么信息通过信道传递的信息量就是互信息 $I(X,Y)$。

条件熵

两个随机变量 X 和 Y 的条件熵定义为
$$\begin{array}{rl}H(Y|X)& =\sum _{x\in X}P(x)H(Y|x)=\sum _{x\in X}P(x)\sum _{y\in Y}P(y|x)log(P(y|x))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(\frac{P(x,y)}{P(x)})\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y))+\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x))\\ & =-\sum _{x\in X}\sum _{y\in Y}P(x,y)log(P(x,y))+\sum _{x\in X}P(x)log(P(x))\\ & =H(X,Y)-H(X)\end{array}$$

条件熵度量了在已知随机变量 X 的条件下随机变量 Y 的不确定性，也即在 X 已知的条件下，获得 Y 对于整体信息量的增加情况，有
$$\begin{array}{rl}H(X,Y)& =H(X)+H(Y|X)\\ & =H(Y)+H(X|Y)\end{array}$$

相对熵（KL 散度)

相对熵（Relative Entropy），也叫 KL 散度 (Kullback-Leibler Divergence)，具有非负的特性。用于衡量两个分布之间距离的指标，用 P 分布近似 Q 的分布，相对熵可以计算这个中间的损失，但是不对称（P 对 Q 和 Q 对P 不相等），因此不能表示两个分布之间的距离，这种非对称性意味着选择 $D_{KL}(P||Q)$ 还是 $D_{KL}(Q||P)$ 影响很大。当 P=Q 时， 相对熵（KL 散度）
取得最小值 。
如果对于同一个随机变量 x 有两个单独的概率分布 $P(x)$ 和 $Q(x)$ ，我们就可以使用 KL 散度来衡量这两个分布的差异。
散度越小，真实分布与近似分布之间的匹配就越好。
$$D_{KL}(P||Q)=E_{x～P}[log\frac{P(x)}{Q(x)}]=E_{x～P}[logP(x)-logQ(x)]$$

https://zhuanlan.zhihu.com/p/46576065111