UWB(Ultra-Wideband)技术是一种短脉冲无线电技术(短脉冲意味着信号的带宽很大，因此称为超宽带)，其应用非常广泛，其中之一就是室内定位，通过计算信号传播的时间差，可以得到标签和基站之间的距离,如果有足够多的基站，就可以通过三角定位等方法计算出标签的位置。如下图所示：

本文将介绍两种利用标签与基站的距离信息求解标签位置的方法，分别是线性最小二乘和非线性优化。

线性最小二乘

对于线性最小二乘方法，假设有$m$个基站，第$i$个基站的坐标为$a_i=(a_{i,1},a_{i,2},a_{i,3})$，标签与第$i$个基站之间的距离为$r_i$，标签的坐标为$x=(x_1,x_2,x_3)$。则可以得到以下方程组：

$$\{\begin{array}{l}(x_1-a_{1,1}{)}^2+(x_2-a_{1,2}{)}^2+(x_3-a_{1,3}{)}^2=r_1^2\\ (x_1-a_{2,1}{)}^2+(x_2-a_{2,2}{)}^2+(x_3-a_{2,3}{)}^2=r_2^2\\ \cdots \\ (x_1-a_{m,1}{)}^2+(x_2-a_{m,2}{)}^2+(x_3-a_{m,3}{)}^2=r_m^2\end{array}$$

使用$a_i$表示第$i$个基站的坐标向量，向量的模表示为：

$$||a_i||=\sqrt{a_{i,1}^2+a_{i,2}^2+a_{i,3}^2}$$

将第二行以及之后的方程减去第一行，可以得到以下方程组：

$$\{\begin{array}{l}2(a_1-a_2{)}^{T}x=r_2^2-r_2^2-||a_2|{|}^2+||a_1|{|}^2\\ 2(a_1-a_3{)}^{T}x=r_3^2-r_1^2-||a_3|{|}^2+||a_1|{|}^2\\ \cdots \\ 2(a_1-a_m{)}^{T}x=r_m^2-r_1^2-||a_m|{|}^2+||a_1|{|}^2\end{array}$$

将上述方程组写成矩阵形式，可以得到：

$$\left[\begin{array}{c}2(a_1-a_2{)}^T\\ 2(a_1-a_3{)}^T\\ ⋮\\ 2(a_1-a_m{)}^T\end{array}\right]x=\left[\begin{array}{c}{r}_2^2-r_2^2-||a_2|{|}^2+||a_1|{|}^2\\ r_3^2-r_1^2-||a_3|{|}^2+||a_1|{|}^2\\ ⋮\\ r_m^2-r_1^2-||a_m|{|}^2+||a_1|{|}^2\end{array}\right]$$

令$A$为上述矩阵，$b$为上述向量，则可以得到以下方程：

$$Ax=b$$

使用矩阵的伪逆求解上述方程，即可得到标签的位置$x$。

非线性优化

非线性优化方法通过最小化标签与基站之间距离的误差来求解标签的位置，优化变量即为标签的位置。

具体来说，假设有$m$个基站，第$i$个基站的坐标为$a_i=(a_{i,1},a_{i,2},a_{i,3})$，标签与第$i$个基站之间的距离为$r_i$，标签的坐标为$x=(x_1,x_2,x_3)$，则标签与第$i$个基站之间距离的误差为：

$$f_i(x)=\sqrt{(x_1-a_{i,1}{)}^2+(x_2-a_{i,2}{)}^2+(x_3-a_{i,3}{)}^2}-r_i$$

将所有基站的误差平方和作为目标函数，即：

$$\underset{x}{\min }\sum _{i=1}^m{f}_i^2(x)$$

该目标函数是一个非线性函数，可以使用非线性最小二乘法进行求解。具体来说，可以使用LM算法(Levenberg-Marquardt算法)对目标函数进行优化，求解出标签的位置$x$。

LM算法

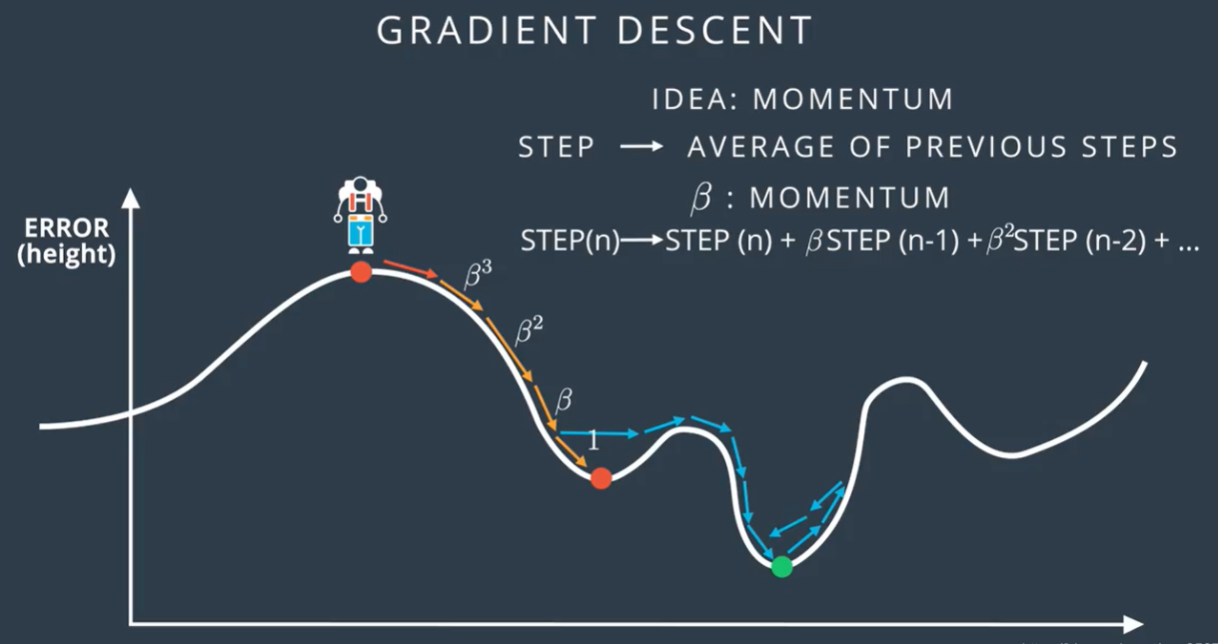
LM算法是一种非线性最小二乘法的优化算法，可以用于求解非线性优化问题。它是一种介于Gauss-Newton算法和梯度下降算法之间的方法，具有收敛速度快、收敛性好等优点。

LM算法的流程如下：

1. 初始化参数$x$，设置初始步长$\lambda$，设置容差$ϵ$，设置最大迭代次数$max\_iter$。
2. 计算误差向量$f(x)$和雅可比矩阵$J(x)$。
3. 计算增量$\Delta x$，其中$\Delta x$满足以下方程：

$$(J^{T}J+\lambda I)\Delta x=-J^{T}f(x)$$

4. 计算新的参数$x_{new}=x+\Delta x$，计算新的误差向量$f(x_{new})$。
5. 如果新的误差向量的平方和小于容差$ϵ$，则停止迭代；否则，判断新的误差向量是否比原来的误差向量更小，如果更小，则减小步长$\lambda$，重复步骤2-5；否则，增加步长$\lambda$，重复步骤2-5。

附录中给出了LM算法的C++实现，其中雅可比矩阵的计算使用了数值微分，也可以使用解析求导的方法进行计算：

$$\frac{\partial f_i}{\partial x_j}=\frac{x_j-a_{i,j}}{\sqrt{(x_1-a_{i,1}{)}^2+(x_2-a_{i,2}{)}^2+(x_3-a_{i,3}{)}^2}}$$

其中$j$为$x$的第$j$个分量，分母表示标签与第$i$个基站之间的距离。

附录：C++实现

本文代码基于Eigen库实现，包含的头文件如下：

#include <Eigen/Core>
#include <Eigen/Dense>

线性最小二乘

以下代码使用线性最小二乘法求解标签的位置，它是一个lambda表达式，输入参数为基站的坐标向量和标签与基站之间的距离，输出为标签的位置。

auto trilateration = [](const std::vector<Eigen::Vector3d>& uwb_stations, const std::vector<double>& uwb_range) {
    Eigen::MatrixXd A(uwb_stations.size() - 1, 3);
    Eigen::VectorXd b(uwb_stations.size() - 1);
    for (int i = 1; i < uwb_stations.size(); i++) {
        A.row(i - 1) = 2 * (uwb_stations[0] - uwb_stations[i]).transpose();
        b(i - 1) = uwb_range[i] * uwb_range[i] - uwb_range[0] * uwb_range[0] - (uwb_stations[i].squaredNorm() - uwb_stations[0].squaredNorm());
    }
    // 使用SVD求解线性最小二乘问题
    Eigen::Vector3d pos = A.jacobiSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);
    return std::vector<double>({pos[0], pos[1], pos[2]});
};

非线性优化

以下代码使用LM算法对上述目标函数进行优化，求解出标签的位置，求导过程使用了数值微分。

// 定义非线性优化问题
struct UWBProblem {
    // 测量值
    std::vector<double> ranges;
    // anchor坐标
    std::vector<std::vector<double>> anchors;
    // 优化变量
    std::vector<double> x;
    // 重载()运算符，计算误差
    int operator()(const double* x, double* fvec) const {
        for (int i = 0; i < ranges.size(); ++i) {
            double r = ranges[i];
            std::vector<double> a = anchors[i];
            double dist = sqrt(pow(x[0] - a[0], 2) + pow(x[1] - a[1], 2) + pow(x[2] - a[2], 2));
            fvec[i] = dist - r;
        }
        return 0;
    }
};

// 非线性最小二乘法求解器
void levenbergMarquardt(UWBProblem& problem, double lambda, double tol, int max_iter) {
    Eigen::VectorXd x = Eigen::Map<Eigen::VectorXd>(problem.x.data(), problem.x.size());
    int n = x.size();
    int m = problem.ranges.size();
    Eigen::VectorXd fvec(m);
    Eigen::MatrixXd J(m, n);
    for (int iter = 0; iter < max_iter; ++iter) {
        // 计算误差向量和雅可比矩阵
        problem(x.data(), fvec.data());
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                double h = 1e-6;
                Eigen::VectorXd x1 = x;
                x1(j) += h;
                Eigen::VectorXd fvec1(m);
                problem(x1.data(), fvec1.data());
                J(i, j) = (fvec1(i) - fvec(i)) / h;
            }
        }
        // 计算增量
        Eigen::MatrixXd JtJ = J.transpose() * J;
        Eigen::VectorXd Jtf = J.transpose() * fvec;
        JtJ.diagonal().array() += lambda;
        Eigen::VectorXd dx = -JtJ.ldlt().solve(Jtf);
        // 更新变量
        Eigen::VectorXd x_new = x + dx;
        // 判断是否收敛
        double err = fvec.squaredNorm();
        if (err < tol) {
            break;
        }
        // 更新lambda
        Eigen::VectorXd fvec_new(m);
        problem(x_new.data(), fvec_new.data());
        double err_new = fvec_new.squaredNorm();
        if (err_new < err) {
            lambda /= 10;
            x = x_new;
            fvec = fvec_new;
        } else {
            lambda *= 10;
        }
    }
    // 更新优化变量
    problem.x = std::vector<double>(x.data(), x.data() + x.size());
}

调用方法如下：

// 设置初始值
vector<double> x0 = {0, 0, 0};
// 设置测量值
std::vector<double> ranges;
// 设置anchor坐标
std::vector<std::vector<double>> anchors;
UWBProblem problem;
problem.ranges = ranges;
problem.anchors = anchors;
problem.x = x0;
// 进行优化
double lambda = 0.1;
double tol = 1e-6;
int max_iter = 1000;
levenbergMarquardt(problem, lambda, tol, max_iter);
// 输出优化结果
std::cout << "x = " << problem.x[0] << ", y = " << problem.x[1] << ", z = " << problem.x[2] << std::endl;