1 最小二乘法估计(LS)
1.1 原理与推导
最小二乘法最早是高斯在预估星体轨道时提出来的,后来成为了估计理论的奠基石。考虑如下CAR模型:
![]()
其中:
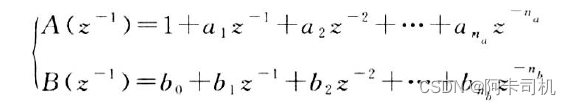
参数估计的任务就是根据输入和输出,估计出a1,a2,----,ana,b1,b2,...,bnb这na+nb+1个参数。
将1-1式改成差分方程形式:
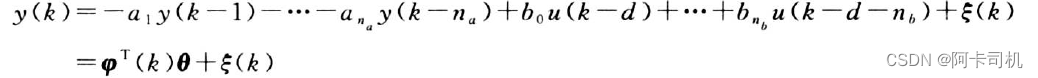

对于L组输入{y(k),u(k),k=1,2,...,L},系统参数的最小二乘估计为:
![]()
其中:
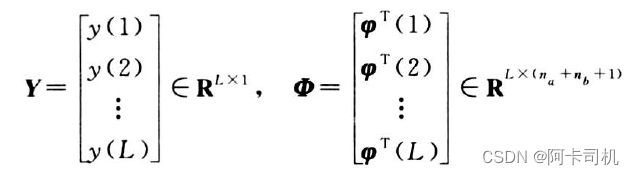
上式推导过程为:
对于第k次测量,其残差为:

构造如下性能指标J:
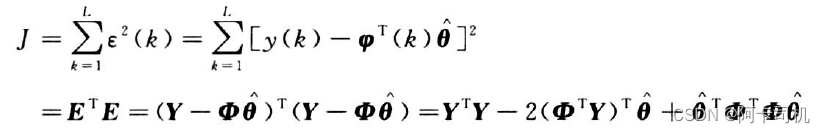
![]()
当J取极小值时,将有:

此时有:
![]()
1.2 例子
考虑如下系统:
![]()
![]()
Matlab程序为:
%最小二乘参数估计(LS)
clear all;
a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次
L=400; %数据长度
uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
x1=1; x2=1; x3=1; x4=0; S=1; %移位寄存器初值、方波初值
xi=sqrt(1)*randn(L,1); %白噪声序列
theta=[a(2:na+1);b]; %对象参数真值
for k=1:L
phi(k,:)=[-yk;uk(d:d+nb)]'; %此处phi(k,:)为行向量,便于组成phi矩阵
y(k)=phi(k,:)*theta+xi(k); %采集输出数据
M=xor(x3,x4); %产生M序列
IM=xor(M,S); %产生逆M序列
if IM==0
u(k)=-1;
else
u(k)=1;
end
S=not(S); %产生方波
%更新数据
x4=x3; x3=x2; x2=x1; x1=M;
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
thetae=inv(phi'*phi)*phi'*y' %计算参数估计值thetae(结果见MATLAB命令窗口)运行结果:
thetae =
-1.5159
0.7206
1.0439
0.4714
2 递推最小二乘法(RLS)
递推最小二乘法RLS是最小二乘法LS的改进版,它可以根据采样的实时数据来不断修正估计参数,从而做到参数的实时估计。其基本思想是:

RLS的实施步骤为:

对于上节中的例子,Matlab程序:
%递推最小二乘参数估计(RLS)
clear all; close all;
a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次
L=400; %仿真长度
uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
u=randn(L,1); %输入采用白噪声序列
xi=sqrt(0.1)*randn(L,1); %白噪声序列
theta=[a(2:na+1);b]; %对象参数真值
thetae_1=zeros(na+nb+1,1); %thetae初值
P=10^6*eye(na+nb+1);
for k=1:L
phi=[-yk;uk(d:d+nb)]; %此处phi为列向量
y(k)=phi'*theta+xi(k); %采集输出数据
%递推最小二乘法
K=P*phi/(1+phi'*P*phi);
thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
P=(eye(na+nb+1)-K*phi')*P;
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
plot([1:L],thetae); %line([1,L],[theta,theta]);
xlabel('k'); ylabel('参数估计a、b');
legend('a_1','a_2','b_0','b_1'); axis([0 L -2 1.5]);运行结果:
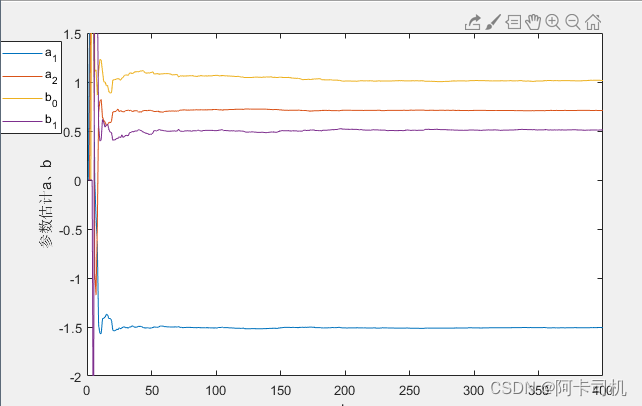
3 遗忘因子最小二乘法(FFRLS)
3.1 FFRLS原理
对于参数时变系统,RLS易出现数据饱和现象,就是随着时间的变化,矫正矩阵P(k)和K(k)越来越小,从而其矫正作用越来越弱,这将导致较大的估计误差。遗忘因子最小二乘法可以较好的处理这个问题。
FFRLS的实施步骤为:

3.2 例子
考虑系统

Matlab程序为:
%遗忘因子递推最小二乘参数估计(FFRLS)
clear all; close all;
a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次
L=2000; %仿真长度
uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
u=randn(L,1); %输入采用白噪声序列
xi=sqrt(0.1)*randn(L,1); %白噪声序列
thetae_1=zeros(na+nb+1,1); %thetae初值
P=10^6*eye(na+nb+1);
lambda=1; %遗忘因子范围[0.9 1]
for k=1:L
if k==501
a=[1 -1 0.4]';b=[1.5 0.2]'; %对象参数突变
end
theta(:,k)=[a(2:na+1);b]; %对象参数真值
phi=[-yk;uk(d:d+nb)];
y(k)=phi'*theta(:,k)+xi(k); %采集输出数据
%遗忘因子递推最小二乘法
K=P*phi/(lambda+phi'*P*phi);
thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
P=(eye(na+nb+1)-K*phi')*P/lambda;
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
subplot(1,2,1)
plot([1:L],thetae(1:na,:)); hold on; plot([1:L],theta(1:na,:),'k:');
xlabel('k'); ylabel('参数估计a');
legend('a_1','a_2'); axis([0 L -2 2]);
subplot(1,2,2)
plot([1:L],thetae(na+1:na+nb+1,:)); hold on; plot([1:L],theta(na+1:na+nb+1,:),'k:');
xlabel('k'); ylabel('参数估计b');
legend('b_0','b_1'); axis([0 L -0.5 2]);当设置遗忘因子为1时,参数估计如图所示有比较大的误差:
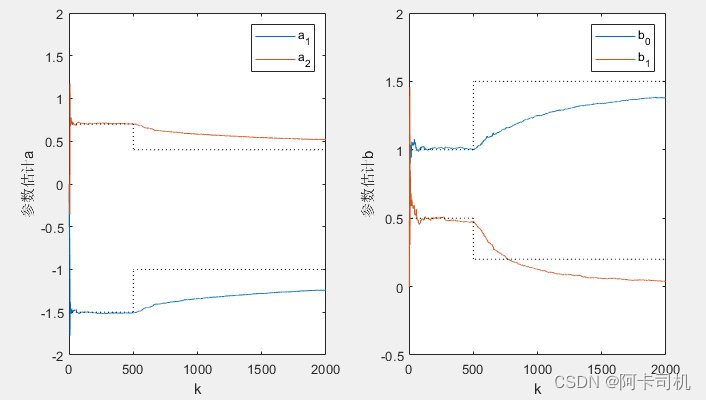
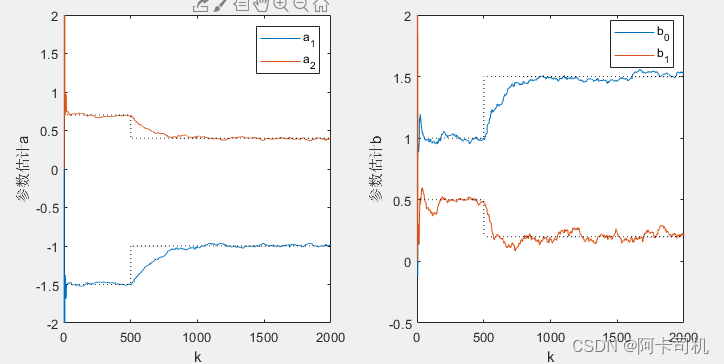
当设置遗忘因子为0.99时,参数估计如图所示:
 4 递推增广最小二乘法(RELS)
4 递推增广最小二乘法(RELS)
4.1 RELS原理
当系统模型的干扰为有色噪声时,系统方程表示为

写成最小二乘形式为:
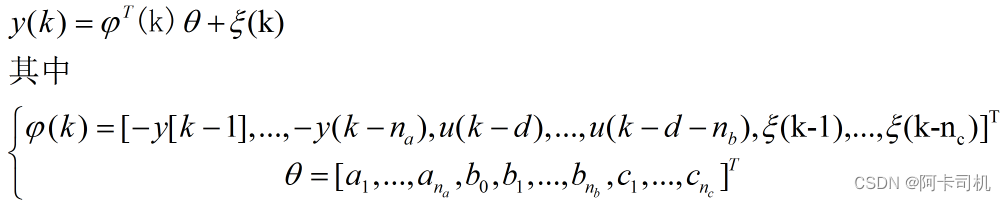
增广最小二乘法 实施步骤:

4.2 例子
.考虑系统
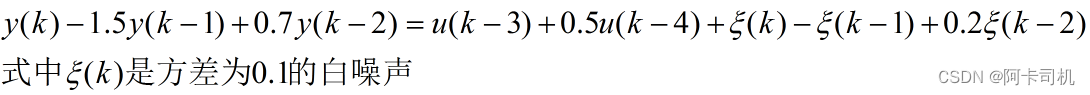
Matlab程序:
%递推增广最小二乘参数估计(RELS)
clear all; close all;
a=[1 -1.5 0.7]'; b=[1 0.5]'; c=[1 -1 0.2]'; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %na、nb、nc为A、B、C阶次
L=1000; %仿真长度
uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
xik=zeros(nc,1); %噪声初值
xiek=zeros(nc,1); %噪声估计初值
u=randn(L,1); %输入采用白噪声序列
xi=sqrt(0.1)*randn(L,1); %白噪声序列
theta=[a(2:na+1);b;c(2:nc+1)]; %对象参数
thetae_1=zeros(na+nb+1+nc,1); %na+nb+1+nc为辨识参数个数
P=10^6*eye(na+nb+1+nc);
for k=1:L
phi=[-yk;uk(d:d+nb);xik];
y(k)=phi'*theta+xi(k); %采集输出数据
phie=[-yk;uk(d:d+nb);xiek]; %组建phie
%递推增广最小二乘法
K=P*phie/(1+phie'*P*phie);
thetae(:,k)=thetae_1+K*(y(k)-phie'*thetae_1);
P=(eye(na+nb+1+nc)-K*phie')*P;
xie=y(k)-phie'*thetae(:,k); %白噪声的估计值
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
for i=nc:-1:2
xik(i)=xik(i-1);
xiek(i)=xiek(i-1);
end
xik(1)=xi(k);
xiek(1)=xie;
end
figure(1)
plot([1:L],thetae(1:na,:));
xlabel('k'); ylabel('参数估计a');
legend('a_1','a_2'); axis([0 L -2 2]);
figure(2)
plot([1:L],thetae(na+1:na+nb+1,:));
xlabel('k'); ylabel('参数估计b');
legend('b_0','b_1'); axis([0 L 0 1.5]);
figure(3)
plot([1:L],thetae(na+nb+2:na+nb+nc+1,:));
xlabel('k'); ylabel('参数估计c');
legend('c_1','c_2'); axis([0 L -2 2]); 运行结果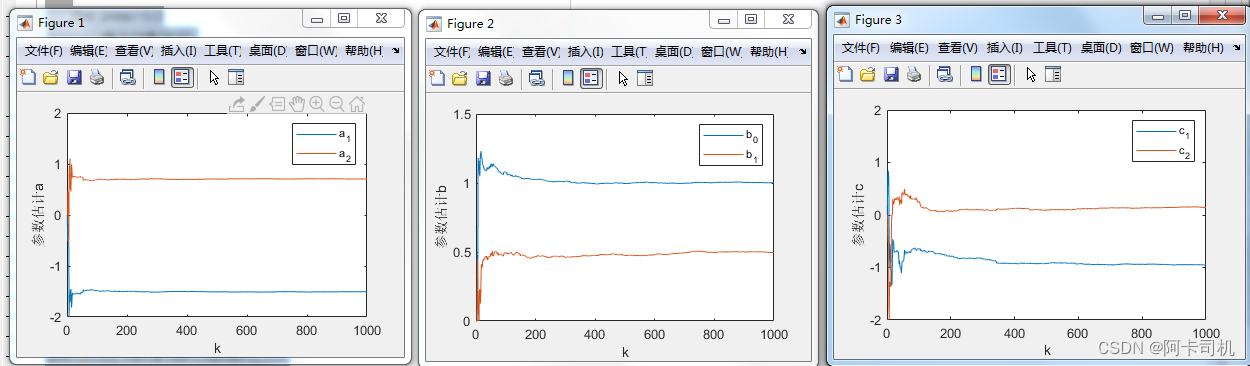
参考:系统辨识与自适应控制Matlab仿真(第3版),庞中华,崔红编著