1.我们如何处理图像分配这个任务

我们要给计算机一张图片，让它识别出这是一只猫？

        通过我之前写的机器学习博客我们知道，系统是知道一些预定信息（标签信息）的，这些可能是狗、猫、卡车或飞机等...，计算机的工作就是根据这张图片的输入并为其分配这些固定类别标签中的一个。

这似乎对于人类是个非常简单的问题，因为我们大脑在帮我们做这些事情，但是当计算机看到这张图片时会看到什么呢？它肯定不会得到你看到的猫的整体概念。

         计算机将图像表达为如上图一样巨大的数字网格，也就是像素，每个像素由三个数字（RGB）表示，并且很难从中提取出猫的特性，我们将这个问题成为语义鸿沟。猫的这个概念，或者猫这个标签是我们分配给这个图像的语义标签。猫的语义概念和计算机实际看到的这些像素值之间存在巨大差距。

这是一个非常困难的问题，因为我们可以以非常细微的方式更改图片。这将导致该像素网格完全改变。

比如我们将相机转到另一个角度拍摄猫。我们的算法需要对此具有鲁棒性。

另外，照明、猫的喜怒都不影响猫就是猫，我们的算法需要对此具有鲁棒性。

    同时，猫的“变形”、物体遮挡、背景杂乱、类内变异....这些都是机器视觉应该考虑到的问题。

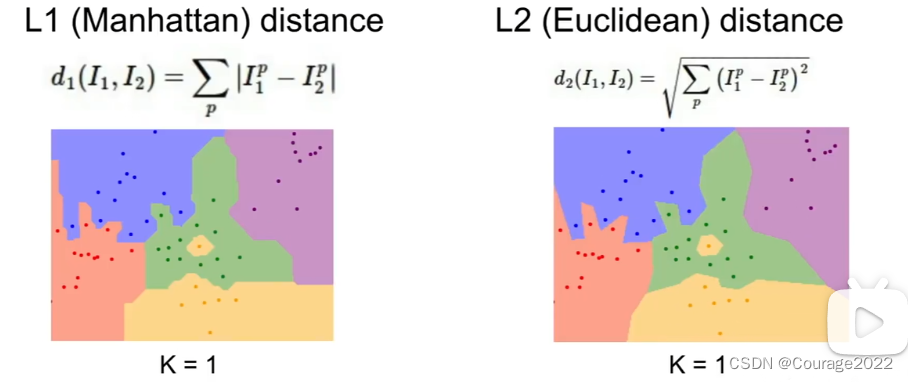
2.图像分类远古方法----利用曼哈顿距离：L1距离

为了对比训练集和测试集，我们引入L1距离：

$d_{1}(I_{1},I_{2})=\sum_{p}^{}|I_{1}^{p}-I_{2}^{p}|$

在测试时，我们将获取我们的图像，然后使用这个L1距离函数将我们的测试图像与这些训练示例中的每一个进行比较，并在训练集中找到最相似的示例。

但是我们有如下问题：

首先，如果我们的训练集中有N个示例，那么我们期望训练和测试的速度有多快？因为我们真的要做任何事情，训练的时间复杂度为 $O(1)$ ，测试的时间复杂度为 $O(N)$ 。因为在测试时，我们需要将我们的测试图像与数据集中的N个训练示例中的每一个进行比较。
但是，在实践中我们希望训练很慢，预测很快，能满足实时性，这样的方法是不可行的。

3.图像分类远古方法----利用欧几里得距离：L2距离

为了对比训练集和测试集，我们引入L2距离：

$d_2(I_{1},I_{2})=\sqrt{\sum_{p}^{}(I_{1}^{p}-I_{2}^{p})^2}$

选择不同的距离度量实际上是一个非常有趣的话题，因为不用的距离度量对你在空间中所期望的底层几何或拓扑做出不同的假设。
其实，旋转图像是可以改变点与点之间的L1距离的坐标系，虽然改变L2距离的坐标系
并不重要，但不管你的坐标系是什么，都是一样的。也许如果你的输入特征如果你的向量中的各个条目对你的任务有一些重要的意义，那么也许L1可能更是适合，但是如果它只是某个空间中的一个通用向量并且你不知道哪些不同的元素的实际含义，那么L2可能会适合一些。

对于k近邻算法，选择不同的距离度量产生的结果也会不一样。边界的形状实际上在两个指标之间发生了相当大的变化。因此，当您查看L1时，这些决策边界往往会遵循坐标轴。
这又是因为L1取决于我们选择的坐标系，L2并不真正关心坐标轴，它只是将边界放在它们应该自然落下的地方。

4.超参数

一旦您实际尝试在实践中使用此算法，需要做出几个选择。我们讨论了选择不同的K值。我们讨论了选择不同的距离度量。问题变成，你怎么为你的问题去选择这些参数？
所以，这些选择，比如K和距离度量，我们称之为超参数。因为它们不一定是从训练数据中去学习的，而是你提前做出的关于你的算法的选择。
选择超参数的基准：

①为训练数据提供最佳准确性或最佳性能（会有过拟合现象，不推荐）
②将数据分为训练集和测试集，选择在测试集上运行好的超参数（不好的策略，因为对于新的数据我们不知道结果如何）

③将数据分为训练集、验证集和测试集，现在我们通常做的是在训练集上使用许多不同的超参数选择来训练我们的算法，在验证集上进行评估，然后选择在验证集上表现最好的超参数集。在完成了所有的开发之后，你将在验证集上使用表现最好的分类器在测试集上运行一次。（good ）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/66380.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！