●素数
素数又称为质数，它指在一个大于1的自然数中，除了1和它自身外，没法被其他自然数整除的数。比1大，但不是素数的数称为合数。0和1既不是素数，也不是合数。因为素数的分布没有明显的规律，所以在程序中一般根据素数的定义来判断该数是否为素数。例如哥德巴赫猜想:哥德巴赫通过大量的数据猜测，所有不小于6的偶数，都可以表示为两个奇素数之和。后人将其称之为“1+1”。并且，对于每个不小于9的奇数，都可以表示为三个奇素数之和。
#include<iostream>
using namespace std;
class isprime {
public:
void isprime1()
{
int k=0;
for (int i = a; i <= b; i++)
{
if(i==2||i==3)
{
k = 1;
}
for (int j = 2; j <= i/2 ; j++)
{
if (i % j == 0)
{
k = 0;
break;
}
else
{
k = 1;
}
}
if (k == 1)
{
cout << i << " ";
}
}
}
int a;
int b;
};
void text()
{
isprime ip;
cout << "请输入一个区间范围：" << endl;
cin >> ip.a >> ip.b;
cout << "该区间范围内的素数有：" << endl;
ip.isprime1();
}
int main()
{
text();
}
●最大公约数
最大公约数和最小公倍数是我们频繁接触的一对数。如果有一个自然数m能被自然数n整除，则称m为n的倍数，b为a的约数。多个自然数公共的约数，叫做这几个自然数的公约数。而公约数中最大的一个，就称为这几个自然数的最大公约数。
计算两个自然数最大公约数的传统算法就是欧几里得的辗转相除法，对于要对多个自然数寻找其最大公约数可以通过多次辗转相除法得到，具体步骤如下：
①已知两自然数m、n，假设m>n；
②计算m除以n，将得到的余数记为r；
③如果r=0，则n为求得的最大公约数，否则执行下面一步；
④将n的值保存到m中，将r的值保存到n中，重复执行步骤②和③，直到r=0，便得到最大公约数；
#include<iostream>
using namespace std;
class max_public_number {
public:
int max_public_number1()
{
int temp;
if (m > n){
m = m;
n = n;
}
else{
temp = m;
m = n;
n = temp;
}
r = m % n;
while (r!= 0) //辗转相除法
{
m = n;
n = r;
r = m % n;
}
return n;
}
void showresult()
{
cout << n << endl;
}
int m;
int n;
int r;
};
void text()
{
max_public_number mpn;
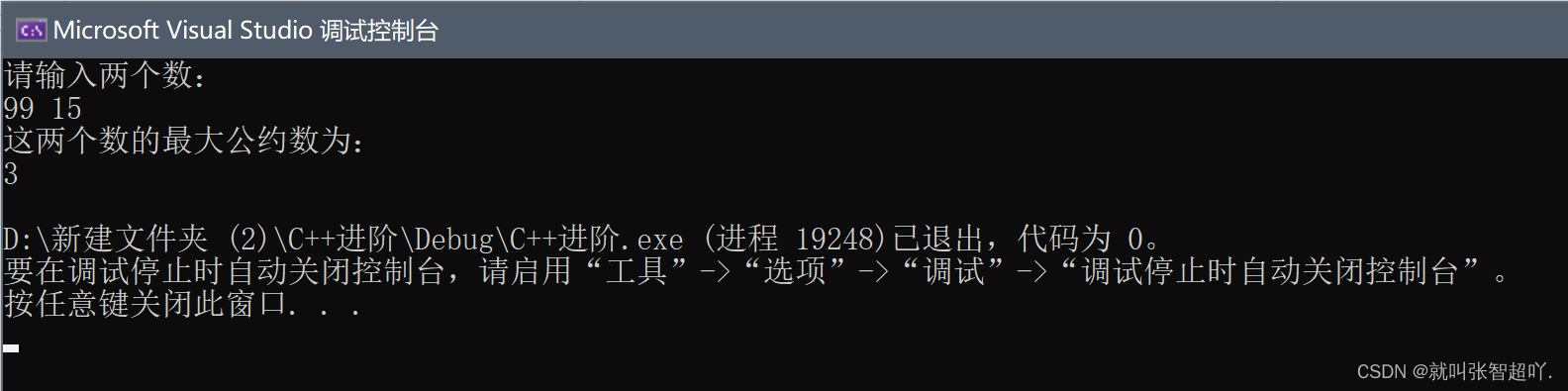
cout << "请输入两个数：" << endl;
cin >> mpn.m>>mpn.n;
cout << "这两个数的最大公约数为：" << endl;
mpn.max_public_number1();
mpn.showresult();
}
int main()
{
text();
}
●完全数
当一个自然数的所有真因子之和等于该自然数，那么该自然数便是完全数（完全数的尾数都是6或8）。
完全数的特殊性质：
1.每个完全数都可以表示成连续自然数的和
2. 每个完全数都是调和级数
3.每个完全数都可以表示为2的一些连续正整数次幂之和
4.除6之外的完全数都可以表示成连续的奇立方之和
#include<iostream>
using namespace std;
class perfectnum {
public:
void perfectnum1()
{
for (int i = 1; i < range; i++)
{
long num = i;
long sum = num; //这里将num赋给sum，在下面num去判断寻找因子，sum去进行逐渐判断是否为完全数
long count = 0; //记数组下标数
for (int j = 1; j < num; j++)
{
if (num % j == 0) //判断j是否为num的真因子
{
p[count++] = j; //若是因子，我们将其记录在数组内
sum -= j; //对sum进行逐减因子
}
}
if (sum == 0) //如果sum能被因子逐减为0，则说明他为完全数
{
cout << "完全数：" << num << endl;
for(int k=0;k<count;k++)
{
cout << p[k] << " "; //输出每个完全数的因子
}
cout << endl;
}
}
}
long p[100];
int range;
};
void text()
{
perfectnum pn;
cout << "请输入一个范围：" << endl;
cin >> pn.range;
cout << "该范围内的完全数为：" << endl;
pn.perfectnum1();
}
int main()
{
text();
}
●亲密数
如果整数a的因子和等于整数b，整数b的因子和等于整数a，因子包括1但不包括本身，且a不等于b，则称a，b为亲密数对。
比如，220的因子为1、2、4、5、10、11、20、22、44、55、110；284的因子为1、2、4、71、142。而220的因子和1+2+4+5+10+11+20+22+44+55+110等于284；284的因子和1+2+4+71+142等于220，并且因子包括1但不包括本身，220不等于284，所以这两数为亲密数对。
#include<iostream>
using namespace std;
class friendnum {
public:
void friendnum1(int i)
{
for(int size=0;size<100;size++) //每次的调用需将数组重复置空
{
a[size] = b[size] = 0;
}
count = 0; //记录数组下标
int sum_1 = 0;
for (int j = 1; j < i / 2 + 1; j++) //求数i的因子
{
if (i % j == 0) //i能被j整除，j为因子
{
a[count++] = j; //保存因子到数组a中
sum_1 += j; //累加因子之和
}
}
count = 0; //置零，重新记录数组下标
int sum_2 = 0;
for (int k = 1; k < sum_1 / 2 + 1; k++) //将数i因子之和sum_1进行因子分解
{
if (sum_1 % k == 0) //sum_1能被k整除
{
b[count++] = k; //保存因子到数组b中
sum_2 += k; //累加因子之和
}
}
if (sum_2 == i && i < sum_1)
{
cout<<sum_2<<"与"<<sum_1<< "是亲密数，" <<"并前两数的因子如下："<< endl;
count = 0;
while (a[count]!=0)
{
cout << a[count] <<" ";
count++;
}
cout << endl;
count = 0;
while(b[count]!=0)
{
cout << b[count] << " ";
count++;
}
cout << endl;
}
}
int a[100];
int b[100];
int range;
int count;
};
void text()
{
friendnum fn;
cout << "请输入一个范围：" << endl;
cin >> fn.range;
cout << "该范围内的亲密数为：" << endl;
for (int a = 1; a <= fn.range; a++)
{
fn.friendnum1(a);
}
}
int main()
{
text();
}
