机器学习使用训练数据进行学习。使用训练数据进行学习,就是针对训练数据计算损失函数的值,也就是说,训练数据有100个的话,就要把这 100个损失函数的总和作为学习的指标。
求多个数据的损失函数,要求所有训练数据的损失函数的综合,可以写成如下式子:
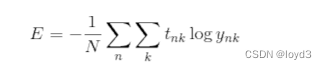
其实就是把求单个数据的损失函数的式子扩大到了N份数据,不过最后还要除以N进行正规化。通过除以N,可以求单个数据的“平均损失函数”。通过这样的均化,可以获得和训练数据的数量无关的统一指标。
在以大数据为对象求损失函数的和,需要花费较长的时间,因此,我们从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch,小批量),然后对每个mini-batch进行学习。
下面来编写从训练数据中随机选择指定个数的数据的代码,以进行mini-batch学习。
import sys,os
sys.path.append(os .pardir)
import numpy as np
from dataset.mnist import load_mnist
# 读人MNIST数据集
(x_train, t train), (x test, t test) =load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape) #(60000,784)
print(t_train.shape) # (60000,10)
train_size =x_train.shape[0]
batch size =10
batch_mask = np.random.choice(train_size,batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
使用np.random.choice()可以从指定的数字中随机选择想要的数字
np.random.choice(60000,10)会从0到59999之间随机选择10个数子,可以得到一个包含被选数据的索引的数组
>>>np.random.choice(60000,10)
array([ 8013,14666, 58210, 23832, 52091, 10153, 8107, 19410, 27262, 14111])
之后,只需指定这些随机选出的索引,取出mini-batch
用随机量数据( mini-batch)作为全体训练数据的近似值。
mini-batch版交叉熵误差的实现
要实现对应mini-batch的交叉误差,需要改良之前实现的单个数据的交叉熵误差,让它可以同时处理单个数据和批量数据(数据作为batch集中输人)
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
这里,y是神经网络的输出,t是监督数据。y的维度为1时,即求单个数据的交叉熵误差时,需要改变数据的形状。并且,当输人为mini-batch时,要用batch的个数进行正规化,计算单个数据的平均交叉熵误差。
此外,当监督数据是标签形式(非one-hot)表示,而是像“2”“7”这样的标签时,交叉熵误差可通过如下代码实现:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + le-7)) / batch_size
实现的要点是,由于one-hot表示中t为0的元素的交叉嫡误差也为0,因此针对这些元素的计算可以忽略。换言之,如果可以获得神经网络在正确解标签处的输出,就可以计算交叉熵误差。
此外关于 np.log(y[np.arange(batch_size), t] + 1e-7)
np.arange(batch_size)会生成一个从0到batch_size-1的数组。因为t中标签是以[2,7,0,9,4]的形式存储的,所以y[np.arange(batch_size), t] 能抽出各个数据的正确解标签对应的神经网络的输出在这个例子中y[np.arange(batch_size), t] 会输出NumPy数组[y[0,2], y[1,7]],y[2,0],y[3,9],y[4,4]]