1、大尺寸卷积存在的问题
当卷积的输入太大导致内存不够用时,考虑将一大块卷积分成多个小块分别进行卷积,相当于将原始输入分成几个小的输入经过同一组卷积核分别卷积,其中每块小的输入都是原始输入的子集,每块之间互不影响,最后将结果合并,实现分块卷积的输出结果与整个输入卷积后的结果完全一致,这种分块卷积的算法可以减小内存消耗同时大大提高运行效率。

但是这种算法有个问题,如果单纯的简单划分的话卷积到后面会越来越少,也就是说会有信息损失。因此在分块的时候会有overlap的出现,并且这个overlap会随着层数的增加会累积。
2、分块卷积overlap产生的来源
经过上面的分析,我们知道分块卷积的时候每两块之间会有overlap的出现,并且这个overlap会随着层数的增加会累积,先看一个简单的例子
-
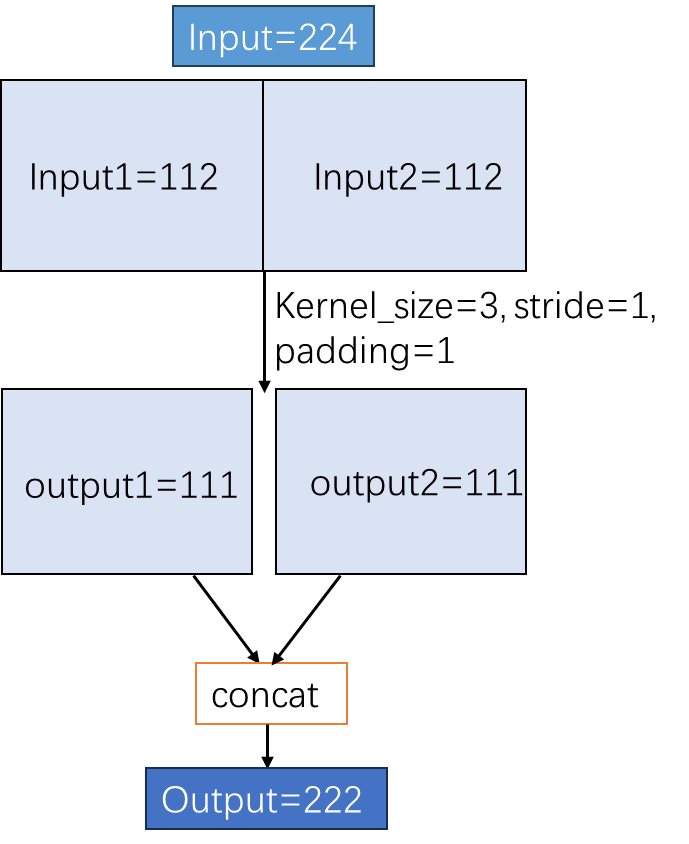
例:输入input shape为[1, 3, 224, 224],kernel_size=3,stride=1,padding=1,只考虑W的卷积情况。经过一层卷积后output shape=(224 - 3 + 2*1)/1 + 1=224。但是将W均分成两块进行卷积的话,output1=(112 - 3 + 1)/1 + 1=111,因为它的padding只有一边,同样output2 的尺寸也是111,将两个结果合并输出为[1, 3, 224, 222],也就是说这样的卷积会有信息损失。
-
下面考虑怎么做才能使得上述例子不会有信息损失,因为卷积是以stride为步长一步一步往后滑动进行计算的,所以分块之后进行卷积的话在分界处卷积核就会跨在了左右两块的边缘,如果要输出与原始卷积结果一致那就需要把跨在边缘的差值分别加在两块边缘,使得左右两块互不干扰并且拼接起来又刚好与原始卷积完全一致,这也就实现了无损失的分块卷积,那么卷积核跨在边缘的差值的多少就是接下来所需讨论的。
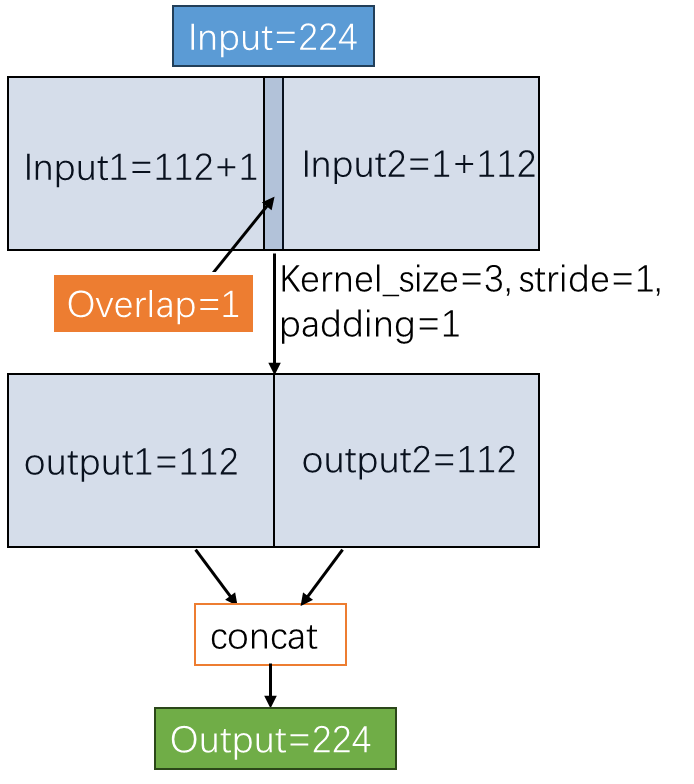
从上面的对比实验可以看出,分块的时候加上overlap即可实现无信息损失的分块卷积。
3、分块卷积overlap的计算
一般来说,先将输入平均分块,然后每一块分别卷积,在分界处考虑跨两块边缘的情况,然后每块加上overlap往下进行卷积;最后从输出向上反推,overlap会以stride的倍数向上累计,直至输入层,计算得出每块真实所需的数量,以这个数量进行分块即可实现与普通卷积完全一致的结果。
如下这个函数就是用来计算输入每块overlap的尺寸。同时支持计算卷积与反卷积(也叫转置卷积)操作的overlap,然后从输出层从下往上反推,输出反推至输入层之后每块的切分尺寸以及每两块之间的重叠区域尺寸。
#!/usr/bin/env python3
# -*-coding:utf-8 -*-
import argparse
import math
def unit_allocation(alist, num, block): # 递归分块函数
if block == 1:
alist.insert(len(alist)//2, num)
return alist
elif block == 2:
alist.insert(len(alist)//2, num//2)
alist.insert(len(alist)//2, num - (num//2))
return alist
alist.insert(len(alist)//2,num//block)
alist.insert(len(alist)//2,num//block)
return unit_allocation(alist,num - (num//block * 2),block - 2)
def overlap_size(unit = 3,file = "Conv_param.csv"):
"""计算重叠区域函数
主要功能:当卷积的参数量太大导致内存不够用时,考虑将一大块卷积分成多个小块进行分别处理,
最后将结果合并,可以减小内存消耗同时大大提高运行效率,这个函数就是用来计算输入每块的尺寸。
对一个卷积进行分块,支持任意切分块数,分别对每一块进行卷积或反卷积,直至输出层。
然后从输出层从下往上反推,输出反推至输入层之后每块的切分尺寸以及每两块之间的重叠区域尺寸。
params:
unit:切分块数.
file:各层卷积或反卷积所需的相应参数.
file::(kernel_size,stride,padding):每层卷积/反卷积的参数尺寸.
file::type:值为 0,1;
0:表示Conv2D卷积,1:表示ConvTranspose反卷积。
unit_allocation:递归分块函数,每块尺寸比整除方式更平均.
return:
倒推计算出每层的切分尺寸和切分的每两块之间的重叠区域
"""
params = []
with open(file,"r") as file:
for line in file.readlines():
params.append(line.replace("\n","").split(","))
print("输入卷积的各层参数:")
for i in range(len(params)):
print(params[i])
print("\t" + "-"*80)
k_size = []
stride = []
padding = []
in_size = [] # 保存正推往下每层的尺寸
conv_type = []
out_size = [] # 保存正推往下每层每块尺寸和前后需要补的尺寸
_unit_size = []
unit_allocation(_unit_size,int(params[1][0]), unit) # 递归平均分块,也可对unit_size手动指定分块
in_size.append(_unit_size)
for i in range(3,len(params)):
k_size.append(int(params[i][0]))
stride.append(int(params[i][1]))
padding.append(int(params[i][2]))
conv_type.append(int(params[i][-1]))
for i in range(0,len(params) - 3): # 通过参数计算每一层的out_size,len(params) - 3是由于file的前两行不需要,最后一层自动推导得出
unit_size = []
fill = []
unit_fill = []
cum_sum = in_size[i][0]
if conv_type[i] == 0: # 如果是卷积,需要先计算前后的重叠区域再进行卷积
insize0 = math.ceil((in_size[i][0] - k_size[i] + padding[i])/stride[i] + 1)
unit_size.append(insize0)
backstep_size0 = k_size[i] + (insize0 - 1)*stride[i]
remainder_0 = backstep_size0 - (in_size[i][0] + padding[i])
fill.append(0 if remainder_0 == k_size[i] - stride[i] else k_size[i] - stride[i] - remainder_0)
if remainder_0 == 0:
unit_fill.append(str(in_size[i][0]) + "+" + str(0))
else:
unit_fill.append(str(in_size[i][0]) + "+" + str(remainder_0))
for j in range(1,unit - 1):
cum_sum += in_size[i][j]
unit_size.append(math.ceil((fill[j - 1] + in_size[i][j] - k_size[i])/stride[i]) + 1)
backstep_size = k_size[i] + (sum(unit_size) - 1)*stride[i]
remainder_i = backstep_size - (cum_sum + padding[i])
fill.append(0 if remainder_i == k_size[i] - stride[i] else k_size[i] - stride[i] - remainder_i)
if remainder_i == 0:
unit_fill.append(str(fill[j - 1]) + "+" + str(in_size[i][j]) + "+" + str(0)) # 保存每块的前后填充值
else:
unit_fill.append(str(fill[j - 1]) + "+" + str(in_size[i][j]) + "+" + str(remainder_i)) # 保存每块的前后填充值
cum_sum += in_size[i][-1]
unit_size.append((fill[-1] + in_size[i][-1] - k_size[i] + padding[i])//stride[i] + 1)
backstep_size1 = k_size[i] + (sum(unit_size) - 1)*stride[i]
unit_fill.append(str(fill[-1]) + "+" + str(in_size[i][-1])) # 保存每块的前后填充值
fill.append(cum_sum + 2*padding[i] - backstep_size1)
elif conv_type[i] == 1: # 如果是反卷积,先计算resize之后的尺寸再进行卷积
zero_padding = (k_size[i] - padding[i] - 1)
insize0 = (in_size[i][0] + zero_padding - k_size[i] + 1) if stride[i] == 1 else (in_size[i][0]*stride[i] + zero_padding - k_size[i] + 1)
unit_fill.append(str(in_size[i][0]) + "+" + str(0))
insize1 = (in_size[i][unit - 1] + zero_padding - k_size[i] + 1) if stride[i] == 1 else ((in_size[i][unit - 1] + 2)*stride[i] - stride[i] + 1 + (zero_padding - stride[i] + 1) - k_size[i] + 1)
unit_size.append(insize0)
for j in range(1,unit - 1):
unit_size.append((in_size[i][j] - k_size[i] + 1) if stride[i] == 1 else ((in_size[i][j] + 2)*stride[i] - stride[i] + 1 - k_size[i] + 1))
unit_fill.append(str(stride[i] + 1) + "+" + str(in_size[i][j]) + "+" + str(0))
unit_fill.append(str(stride[i] + 1) + "+" + str(in_size[i][-1]))
unit_size.append(insize1)
else:
pass
in_size.append(unit_size)
out_size.append(unit_fill)
layers = len(k_size) - 1 # 层数(从0开始计)
expert1 = []
if conv_type[-1] == 0: # 计算倒数第一层反推的尺寸,计算其他层反推的尺寸需要往前用到最后一层的值递推
expert1.append(k_size[-1] + (in_size[-1][0] - 1)*stride[-1] - padding[-1])
for j in range(1,unit - 1):
expert1.append(k_size[-1] + (in_size[-1][j] - 1)*stride[-1])
expert1.append(k_size[-1] + (in_size[-1][unit - 1] - 1)*stride[-1] - padding[-1] + int(fill[-1]))
elif conv_type[-1] == 1:
zero_padding = (k_size[-1] - padding[-1] - 1)
if stride[-1] == 1:
expert1.append(in_size[-1][0] + k_size[-1] - 1 - zero_padding)
for j in range(1,unit - 1):
expert1.append(in_size[-1][j] + k_size[-1] - 1)
expert1.append(in_size[-1][unit - 1] + k_size[-1] - 1 - zero_padding)
else:
expert1.append((in_size[-1][0] + k_size[-1] - 1 - zero_padding)//stride[-1])
for j in range(1,unit - 1):
expert1.append((in_size[-1][j] + k_size[-1] - 1 + stride[-1] - 1)//stride[-1])
expert1.append((in_size[-1][unit - 1] + k_size[-1] - 1 + stride[-1] - 1 -(zero_padding - stride[-1] + 1))//stride[-1])
else:
pass
overlap1 = list(map(lambda x: x[0]-x[1], zip(expert1, in_size[-2])))
expert = [expert1]
overlap = [overlap1]
remaining = []
for i in range(layers - 1,-1,-1): # 从后往前递推,求出递推回去每一层每一块的尺寸,求后一层的尺寸均需用到前一层的尺寸
expert_i = []
if conv_type[i] == 0:
expert_i.append(k_size[i] + (expert[layers - i - 1][0] - 1)*stride[i] - padding[i])
for j in range(1,unit - 1):
expert_i.append(k_size[i] + (expert[layers - i - 1][j] - 1)*stride[i])
expert_i.append(k_size[i] + (expert[layers - i - 1][unit - 1] - 1)*stride[i] - padding[i])
elif conv_type[i] == 1:
zero_padding = (k_size[i] - padding[i] - 1)
if stride[i] == 1:
expert_i.append(expert[layers - i - 1][0] + k_size[i] - 1 - zero_padding)
for j in range(1,unit - 1):
expert_i.append(expert[layers - i - 1][j] + k_size[i] - 1)
expert_i.append(expert[layers - i - 1][unit - 1] + k_size[i] - 1 - zero_padding)
else:
expert_i.append((expert[layers - i - 1][0] + k_size[i] - 1 - zero_padding)//stride[i])
for j in range(1,unit - 1):
expert_i.append((expert[layers - i - 1][j] + k_size[i] - 1 + stride[i] - 1)//stride[i])
expert_i.append((expert[layers - i - 1][unit - 1] + k_size[i] - 1 + stride[i] - 1 -(zero_padding - stride[i] + 1))//stride[i])
else:
pass
expert.append(expert_i)
overlap_i = list(map(lambda x: x[0]-x[1], zip(expert[layers - i], in_size[i])))
overlap.append(overlap_i)
expert.insert(0, in_size[-1])
overlap.insert(0, list(map(lambda x: x[0]-x[1], zip(in_size[-1], in_size[-1]))))
# print("out_size:",out_size)
if conv_type[-1] == 0: # 计算从最后一层开始,往前递推时每层的尺寸以及前后的overlap尺寸
out_0 = [int(out_size[-1][0].split("+")[-1])]
for j in range(1,unit - 1):
out_0.append(int(out_size[-1][j].split("+")[0]))
out_0.append(int(out_size[-1][j].split("+")[-1]))
out_0.append(int(out_size[-1][-1].split("+")[0]))
elif conv_type[-1] == 1:
out_0 = [overlap[1][0]]
for j in range(1,unit - 1):
out_0.append(overlap[1][j])
out_0.append(0)
out_0.append(overlap[1][-1])
else:
pass
out_overlap = [out_0]
tag = -1
for i in range(layers-1,-1,-1):
out_i = []
if conv_type[i] == 0: # 找出每一块前后的填充尺寸,如果是卷积的情况,需要把上一轮的填充尺寸累加
out_i.append(out_overlap[layers - i - 1][0]*stride[i] + int(out_size[i][0].split("+")[-1]))
for j in range(1,len(out_0) - 1,2):
out_i.append(out_overlap[layers - i - 1][j]*stride[i] + int(out_size[i][(j+1)//2].split("+")[0]))
out_i.append(out_overlap[layers - i - 1][j+1]*stride[i] + int(out_size[i][(j+1)//2].split("+")[-1]))
out_i.append(overlap[layers - i + 1][-1])
elif conv_type[i] == 1: # 如果是反卷积,当前层的overlap即为填充尺寸
out_i.append(overlap[layers - i + 1][0])
for j in range(1,len(out_0) - 1,2):
out_i.append(overlap[layers - i + 1][(j+1)//2])
out_i.append(0)
out_i.append(overlap[layers - i + 1][-1])
else:
pass
out_overlap.append(out_i)
outs = [] # 处理每层倒推的overlap,写成 前面overlap+每块尺寸+后面overlap 的形式
_in = in_size[-1:-len(in_size)-1:-1][1:len(in_size)]
tag = -1
for i in range(len(_in)):
outs_i = []
outs_i.append("{0}+{1}".format(str(_in[i][0]),str(out_overlap[i][0])))
for j in range(1,len(out_overlap[0]) - 1,2):
outs_i.append("{0}+{1}+{2}".format(out_overlap[i][j],_in[i][(j+1)//2], str(out_overlap[i][j + 1])))
outs_i.append("{0}+{1}".format(str(out_overlap[i][-1]),_in[i][-1]))
outs.append(outs_i)
return in_size[-1:-len(in_size)-1:-1],expert[-1:-len(overlap)-1:-1],overlap[-1:-len(overlap)-1:-1],conv_type[-1:-len(conv_type)-1:-1],out_size,outs[-1:-len(outs)-1:-1]
(_in_size,_expert,_overlap,_type,_out_size,_out) = overlap_size(unit = 3, file="Conv_param_1.csv")
is_trans = []
for item in _type[-1:-len(_type)-1:-1]:
if item == 0:
is_trans.append(str(" 卷积"))
elif item == 1:
is_trans.append(str("反卷积"))
print(" 每层的输入尺寸 \t 每层前后的重叠区域 \t每层倒推的切分尺寸 \t倒推的重叠尺寸")
for i in range(len(_type)):
print("第{0}层{1}:{2}\t{3}\t{4}\t{5}".format(i+1,is_trans[i],_in_size[len(_in_size) - i -1],_out_size[i],_expert[i],_out[i]))
# print("第{0}层{1}:{2}\t{3}\t{4}\t{5}\t{6}".format(i+1,is_trans[i],in_shape[len(in_shape) - i -1],out_shape[i],exp[i],ol1[i],out[i]))
# print("第{0}层{1}的输入尺寸:{2} 每一层所需的overlap:{3} 倒推的切分尺寸:{4} 重叠的尺寸:{5}".format(i+1,is_trans[i],in_shape[i],out_shape[i],exp[i],ol1[i]))
print("最后一层的输出尺寸:{0} 倒推的切分尺寸:{1} 重叠的尺寸:{2}".format(_in_size[0],_expert[-1],_overlap[-1]))
例如输入为[1, 3, 224, 224],连着三层卷积,第一层参数为:kernel_size=3,stride=1,padding=1;第二层参数为:kernel_size=4,stride=2,padding=1;第三层参数为:kernel_size=4,stride=2,padding=1。经过三层卷积后输出尺寸为112。
如果分成[74, 76, 74]3块进行卷积的话,每一层正推前后overlap的尺寸,倒推的overlap尺寸以及每块的真实输入尺寸如下图所示。从下图可以看出,如果输入为[76,84,80],经过上述三层卷积之后输出再concat的结果与普通卷积的结果完全一致。
用pytorch的代码验证一下:
import torch
torch.manual_seed(0) # 为CPU设置随机种子
inputs = torch.randn([1, 3, 224, 224])
weight1 = torch.randn([32, 3, 3, 3])
weight2 = torch.randn([64, 32, 4, 4])
weight3 = torch.randn([3, 64, 4, 4])
# 普通卷积,三层之后的结果
def Convolution(x, w1,w2,w3):
y1 = torch.nn.functional.conv2d(x, w1, stride=1, padding=1)
y2 = torch.nn.functional.conv2d(y1, w2, stride=2, padding=1)
y3 = torch.nn.functional.conv2d(y2, w3, stride=2, padding=1)
return y3
# 分块卷积,三层之后的结果
def Block_convolution(x, w1,w2,w3):
x1 = x[:, :, 0:74+2, :]
x2 = x[:, :, 74-6:74+76+2, :]
x3 = x[:, :, 74+76-6:, :]
pad1 = torch.nn.ZeroPad2d([1, 1, 1, 0])
pad2 = torch.nn.ZeroPad2d([1, 1, 0, 0])
pad3 = torch.nn.ZeroPad2d([1, 1, 0, 1])
x1 = pad1(x1)
x2 = pad2(x2)
x3 = pad3(x3)
y1_1 = torch.nn.functional.conv2d(x1, w1, stride=1, padding=0)
y1_2 = torch.nn.functional.conv2d(x2, w1, stride=1, padding=0)
y1_3 = torch.nn.functional.conv2d(x3, w1, stride=1, padding=0)
y1_1 = pad1(y1_1)
y1_2 = pad2(y1_2)
y1_3 = pad3(y1_3)
y2_1 = torch.nn.functional.conv2d(y1_1, w2, stride=2, padding=0)
y2_2 = torch.nn.functional.conv2d(y1_2, w2, stride=2, padding=0)
y2_3 = torch.nn.functional.conv2d(y1_3, w2, stride=2, padding=0)
y2_1 = pad1(y2_1)
y2_2 = pad2(y2_2)
y2_3 = pad3(y2_3)
y3_1 = torch.nn.functional.conv2d(y2_1, w3, stride=2, padding=0)
y3_2 = torch.nn.functional.conv2d(y2_2, w3, stride=2, padding=0)
y3_3 = torch.nn.functional.conv2d(y2_3, w3, stride=2, padding=0)
y = torch.cat([y3_1, y3_2, y3_3], dim=2)
return y
out1 = Convolution(inputs, weight1, weight2, weight3)
out2 = Block_convolution(inputs, weight1, weight2, weight3)
print(out1.shape)
print(out2.shape)
print(torch.allclose(out1, out2)) # 判断两个tensor是否相等
输出:
torch.Size([1, 3, 56, 56])
torch.Size([1, 3, 56, 56])
True
4、结论
由上述示例可以看出,如果输入为[74+2,6+76+2,6+74],经过上述三层卷积之后输出再concat的结果与普通卷积的结果完全一致,也就是说利用这种分块卷积的思想,当卷积的输入太大时可以减少内存占用,同时加速卷积的计算。