1. 引言
2019年是ZKP方案创新井喷的一年。
2019年10月,Chiesa在#zk0x04上的分享 State of the SNARG-scape - Alessandro Chiesa (UC Berkeley, StarkWare, Zcash),有:

根据reference string的类型,可将zk-SNARKs分类为:
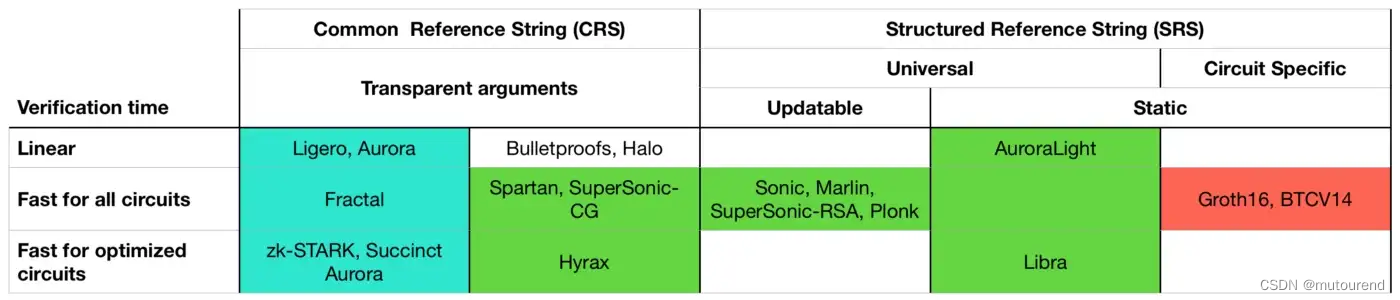
所有zk-SNARKs底层都使用以下3种compilers之一:【下图颜色与上图颜色对应】
- Preprocessing SNARK compiler
- DARK compiler
- traditional compile(即基于static circuit specific reference strings的zk-SNARK方案)
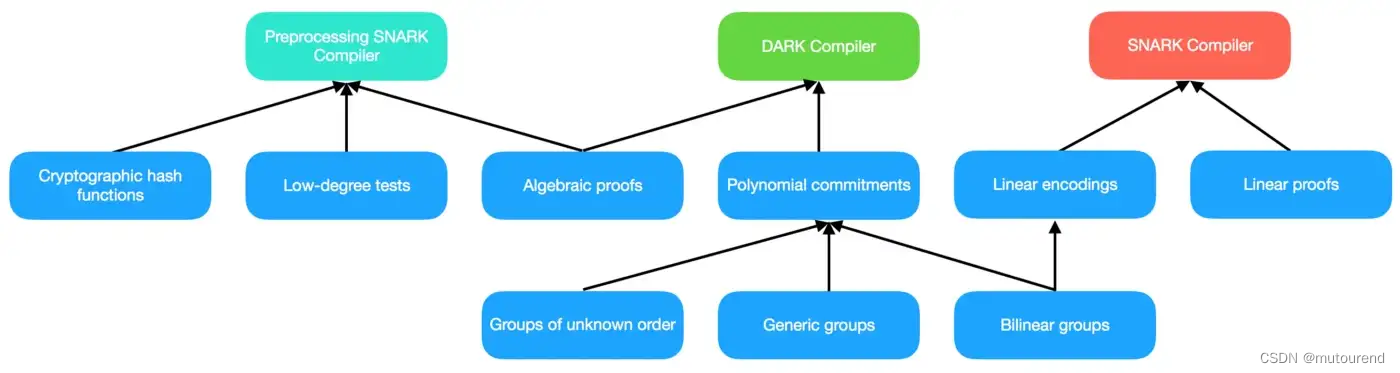
截止到2019年底,主要的ZKP方案有:
- 1)Groth16:见Jens Groth 2016年发表论文 On the Size of Pairing-based Non-interactive Arguments。
Groth16为当前已知的最快最小的zk-SNARK。已用于Zcash。
Groth16为non-universal的,其setup与某个指定circuit紧密关联。由于其速度快和proof size小,很多新的zk-SNARK都会对Groth进行对比。 - 2)Sonic:为早期的通用zk-SNARK协议。见Mary Maller等人2019年论文Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updateable Structured Reference Strings。
Sonic支持universal且updatable common reference string。
Sonic proof size为constant的,但验证开销昂贵。
理论上,可打包验证多个证明以实现更好的性能。 - 3)Fractal:见Chiesa等人2019年论文Fractal: Post-Quantum and Transparent Recursive Proofs from Holography。
Fractal无需pairing-friendly椭圆曲线,且支持递归。
通过对电路进行预处理,可在transparent setup的情况下实现succinct verification。
Fractal的proof size当前为250kB,比其它方案要大,后续该size将进一步降低。 - 4)Halo:见Sean Bowe等人2019年论文Recursive Proof Composition without a Trusted Setup。
Halo为无需trusted setup,支持递归证明组合的zk-SNARK方案。递归采用“nested amortization”:基于cycles of elliptic curves 重复压缩多个证明。
Halo的verification time为linear的,使得其verification不是succinct的。但是后续可进一步改进。 - 5)SuperSonic:见Bunz等人2019年论文Transparent SNARKs from DARK Compilers。
SuperSonic为对Sonic的改进。
SuperSonic是具有实用prover time、近似logarithmic proof size以及实用verification time的首个transparent zk-SNARK。 - 6)Marlin:见Chiesa等人2019年论文Marlin: Preprocessing zkSNARKs with Universal and Updatable SRS。
Marlin为对Sonic的改进。
Marlin的prover time要比Sonic快10倍,Verification time也比Sonic快4倍。 - 7)Plonk:见Gabizon 2019年论文PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge。
Plonk为对Sonic的改进。
Plonk的prover time比Sonic快5倍。 - 8)STAKR: 见Ben-Sasson等人 2018年论文《Scalable, transparent, and post-quantum secure computational integrity》。
相应的性能对比为:
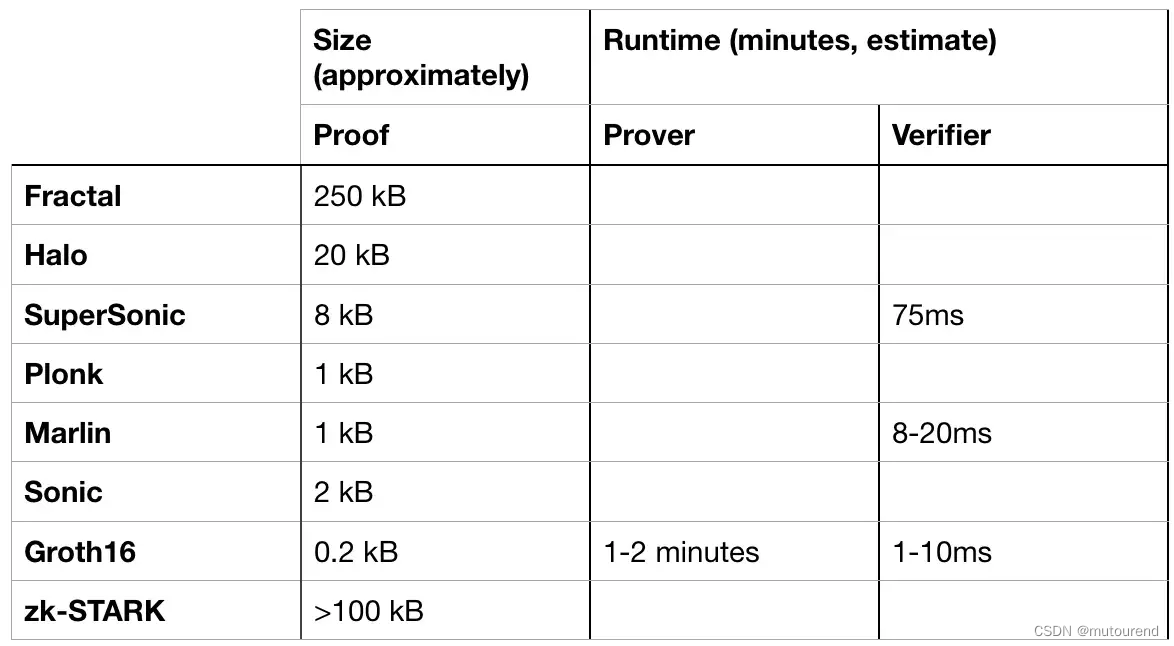
通常来说:
- 1)transparent setup方案具有更大的proof size;
- 2)Halo的Verification time为非constant的;
- 3)Groth16在proof size和runtime方面,仍具有无可匹敌的优势。
参考资料
[1] Comparing General Purpose zk-SNARKs
[2] Evolution of zk-proofs






![[思考进阶]02 如何进行认知升级?](https://img-blog.csdnimg.cn/5f36ccd62eb9467c85e63a4d18f9336b.png#pic_center)