CP121 买股票的最佳时机
题目描述:
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
学习记录:
第一想法是双指针往中间走,但是存在问题,就是取到最大最小的地方我们不知道,无法判断指针的移动,这种方法不可行。还是老老实实用数组记录每一个下标处能获得的最大利润就行,然后找到这个数组的最大即可,可省略为一个存储空间,直接记录最大即可
//超简略一遍过!
class Solution {
public:
int maxProfit(vector<int>& prices) {
int min_value=prices[0];
int result=0;
for(int i=0;i<prices.size();i++)
{
min_value=min(min_value,prices[i]);
result=max(result,prices[i]-min_value);
}
return result;
}
};CP122 买股票的最佳时机II
题目描述:
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回你能获得的最大利润 。
学习记录:
1.动态规划
想不出来转移函数...

 今天没有股票=昨天没有股票OR昨天有然后卖了;今天有=昨天有OR昨天没有今天买了;
今天没有股票=昨天没有股票OR昨天有然后卖了;今天有=昨天有OR昨天没有今天买了;
//题解
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp[n][2];
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}; 简化一下
//题解
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < n; ++i) {
int newDp0 = max(dp0, dp1 + prices[i]);
int newDp1 = max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
};2.贪心法
其实我的思路应该是贪心法,没意识到,我想的是,就是只要能够获得利润,我就卖出,因为买入和卖出可以在同一天进行所以一定能获得更多的利润,但是不确定是不是最优
//题解
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int n = prices.size();
for (int i = 1; i < n; ++i) {
ans += max(0, prices[i] - prices[i - 1]);
}
return ans;
}
};

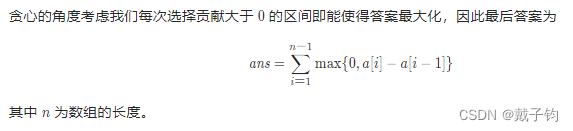
这里解决我刚才的疑惑,就是是否是最佳的。

CP123 买股票的最佳时机III
题目描述:
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
学习记录:
参考刚刚II的想法,然后没有思路....




//题解
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int buy1 = -prices[0], sell1 = 0;
int buy2 = -prices[0], sell2 = 0;
for (int i = 1; i < n; ++i) {
buy1 = max(buy1, -prices[i]);
sell1 = max(sell1, buy1 + prices[i]);
buy2 = max(buy2, sell1 - prices[i]);
sell2 = max(sell2, buy2 + prices[i]);
}
return sell2;
}
};CP188 买股票的最佳时机IV
题目描述:
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格,和一个整型 k 。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
学习记录:
有思路和III一样的用n组selli和buyi来记录,其实刚刚III中的buy1,buy2,其实是buy[i]1,buy[i]2,也就是对应这里的buy[i][j],因为之和前一天的有关系,就压缩到一个存储空间了。

注意:

//题解
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.empty()) {
return 0;
}
int n = prices.size();
k = min(k, n / 2);
vector<vector<int>> buy(n, vector<int>(k + 1));
vector<vector<int>> sell(n, vector<int>(k + 1));
buy[0][0] = -prices[0];
sell[0][0] = 0;
for (int i = 1; i <= k; ++i) {
buy[0][i] = sell[0][i] = INT_MIN / 2;
}
for (int i = 1; i < n; ++i) {
buy[i][0] = max(buy[i - 1][0], sell[i - 1][0] - prices[i]);
for (int j = 1; j <= k; ++j) {
buy[i][j] = max(buy[i - 1][j], sell[i - 1][j] - prices[i]);
sell[i][j] = max(sell[i - 1][j], buy[i - 1][j - 1] + prices[i]);
}
}
return *max_element(sell[n - 1].begin(), sell[n - 1].end());
}
};简化到一个存储空间:
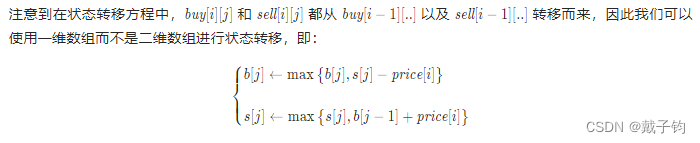
//题解
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.empty()) {
return 0;
}
int n = prices.size();
k = min(k, n / 2);
vector<int> buy(k + 1);
vector<int> sell(k + 1);
buy[0] = -prices[0];
sell[0] = 0;
for (int i = 1; i <= k; ++i) {
buy[i] = sell[i] = INT_MIN / 2;
}
for (int i = 1; i < n; ++i) {
buy[0] = max(buy[0], sell[0] - prices[i]);
for (int j = 1; j <= k; ++j) {
buy[j] = max(buy[j], sell[j] - prices[i]);
sell[j] = max(sell[j], buy[j - 1] + prices[i]);
}
}
return *max_element(sell.begin(), sell.end());
}
};CP309 最佳买卖股票时机含冷冻期
题目描述:
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
学习记录:
一遍过,代码:
可以看到备注的情况,就是定义四种状态,sell,buy,nothing,cold,代表每天可能处于的情况,写出转移方程即可。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int length=prices.size();
if(length==1) return 0;
int result;
//buy:今天买 sell:今天卖
//nothing:今天有股票不做事情 cold:今天没股票但不做事情
int buy=-prices[0],sell=0,nothing=-prices[0],cold=0;
int temp;
for(int i=1;i<length;i++)
{
temp=sell;
sell=max(max(buy,nothing)+prices[i],sell);
nothing=max(buy,nothing);
buy=cold-prices[i];
cold=temp;
}
return sell;
}
};题解:可以看到题解定义的情况比我们少一种,是从当前手上有没有股票来进行定义的
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.empty()) {
return 0;
}
int n = prices.size();
// f[i][0]: 手上持有股票的最大收益
// f[i][1]: 手上不持有股票,并且处于冷冻期中的累计最大收益
// f[i][2]: 手上不持有股票,并且不在冷冻期中的累计最大收益
vector<vector<int>> f(n, vector<int>(3));
f[0][0] = -prices[0];
for (int i = 1; i < n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]);
f[i][1] = f[i - 1][0] + prices[i];
f[i][2] = max(f[i - 1][1], f[i - 1][2]);
}
return max(f[n - 1][1], f[n - 1][2]);
}
};
PS:
就是很难想到转移方程,感觉转移方程有两种情况
1.逻辑关系,比如之前的走格子,你要么....要么....
2.如这几题的情况,考虑你的状态,你每次做完一个操作处在什么状态,每个状态之间是如何进行转变的,最后在哪个状态下取到你想要的结果