一、“变量”的概念
一个代数表达式(通常只有一个字母:x,y,z…,如果它取代了一个未知值(物理、经济、时间等),则称为“变量”。
变量的作用是占据一个值所在的位置,如果该值可用的话。
比如我们有这样一个问题,如果税率是40%,一个人需要缴纳多少税款?
为了回答这样的问题需要了解此人的年薪。由于工资是未知的,我们用一个变量代替它。例如,如果我们定义变量 x = 此人的工资。
他将缴纳40%的税款,即。税款 = 40%x = 0.4x。因此,变量x在税收计算中占据了工资的位置。
二、数学建模示例
数学建模(mathematics modeling)是指创建真实场景的数学表示以进行预测或提供见解的过程。与单纯的拿公式进行使用不同,数学建模是实际寻找并创建数学关系。
数学建模是一个迭代的问题解决过程,在这个过程中,数学被用来探索和加深对现实世界问题的理解。
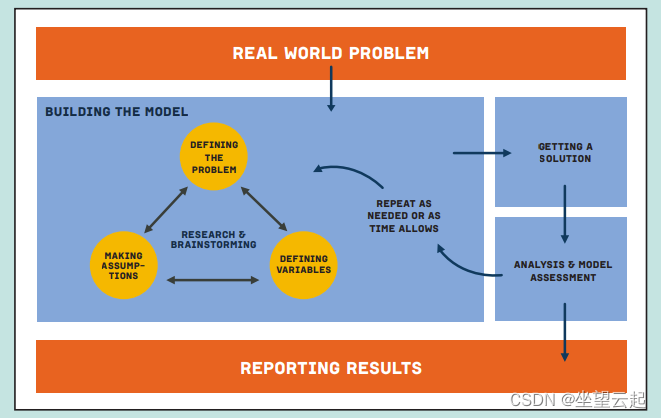
我们使用数学表达式来描述真实的定量情况的过程称为建模。建模包括用数学术语写出首先用语言表达的内容,必要时使用变量。前面的例子说明了建模:尽管我们不知道个人的工资,但我们仍然能够获得一个充分代表他所缴纳税款的表达式。
1、示例1
老王希望投资一只年回报率为10%的股票。到年底他会有多少钱?
老王的初始投资未知。
让我们定义一下:
x:老王投资于该股票的金额
年末累计金额为
x+(10%)x = x+0.1x = 1.1x
看到这里你可能会骂,着什么破玩意,这不就是简单的代数么?是的,确实是这样,例子简单,但是这就是数学建模的核心。
当然,现实世界的问题复杂程度远超于此。
2、示例2
木匠自己生产和销售家具。松木桌子售价650美元,樱桃木桌子售价750美元,枫木桌子售价850美元。木匠的年收入是多少?
木匠的年收入只有在知道每种桌子的销售量的情况下才能获得。因此,变量必须取代这些暂时未知的量。
让我们定义一下:
x = 一年中出售的松木桌子的数量
y = 一年中售出的樱桃餐桌数量
z = 一年中售出的枫木桌子的数量
每张松木桌子的收入为650美元。如果出售x松木桌子,将获得650x的收入。同样的参数也适用于其他类型的表。因此
总收入 = 650x + 750y + 850z
3、示例3
一个项目的三个阶段必须按顺序进行,这意味着一个阶段不能在前一阶段完成之前开始。我们知道,每个阶段的成本分为固定成本和可变成本,固定成本与持续时间无关,可变成本取决于持续时间。
下表总结了情况(这里我们暂不考虑数字的单位):
| 项目阶段 | 1 | 2 | 3 |
| 固定成本 | 318000 | 212000 | 220000 |
| 可变成本 | 15000/天 | 14000/天 | 16000/天 |
该项目的经理必须计算该项目的费用。他希望确定一个费用,以确保至少10%的利润率。表达项目的总成本和设计师应在每个阶段的持续时间内提出的价格。
每个阶段的持续时间未知。因此,让我们定义以下三个变量:
x = 阶段1的持续时间,单位天
y = 阶段2的持续时间,单位天
z = 阶段3的持续时间,单位天
第一阶段的成本可分为固定成本(318000)和可变成本(每天15000)。
如果第1阶段持续x天,则该阶段的费用为
阶段1花费 = 318000 + 15000x
同样的原则适用于其他两个阶段。
项目的总成本可以表示为三个阶段的成本之和:
总花费 = (318000 + 15000x) + (212000+ 14000y)+(220000 + 16000z)
该项目的拟议价格必须确保有10%的利润率,因此,价格必须至少比总成本高出10%:
总费用 >= 1.1 * ((318000 + 15000x) + (212000+ 14000y)+(220000 + 16000z))
4、示例4
一个没有盖子的方形底部盒子由一种材料制成,侧面每平方米0.75元,底部每平方米0.95元。根据盒子的宽度和高度来表示建造盒子所需材料的总成本。
为了计算所需材料的成本,我们必须确定盒子每一侧及其底部的表面积(以平方米为单位)。这个盒子的尺寸目前还未知。
我们进行如下定义
x = 盒子底部长度,单位米
y = 盒子的高度,单位米
盒子的四边各有一平方米的面积。因此,每一面的材料成本为0.75xh。
盒子底部的面积为 x*x 平方米。底部的材料成本为。因此,建造盒子所需材料的总成本由下式给出:
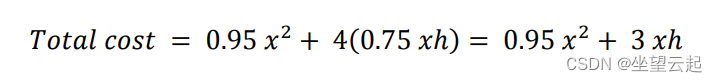
有些问题在不同变量之间存在约束。让我们以示例2的上下文为例。在这里,x和y的值是完全自由的。然而,枫木的短缺可能迫使木匠生产的枫木桌子是樱桃桌子的一半。这种约束也可以使用表达式在数学符号中建模z=(1/2)y 或 y=2z。
当一个问题被建模时,考虑所有给定的信息是很重要的。这样,所有的量值(物理的、经济的、时间的)和所有的约束都必须转化为数学语言。
5、示例5
一位农民正打算划分土地以种植不同的作物。假设,玉米地每平方米的收益为3.50元。燕麦田每平方米收益2.75元。果园的收入为每平方米4.50元。这个农民有100万平方米的土地。为了喂养他的农场动物,耕种者必须至少投入30万平方米用于玉米和燕麦的种植。然而,由于玉米更容易受到长期干旱的影响,他不希望这作物化占地超过20万平方米。最后,他希望将同样数量的土地分配给燕麦和果园。
如何正确地表述农民的收入?这就要求我们需要基于所有约束条件进行建模。
为了对这个问题进行完整的建模,必须确定三个未知因素:
x = 玉米的面积
y = 燕麦的面积
z = 果园的面积
收入以每种作物所占据的面积和每平方米的收益来表示
总收入 = 3.5x + 2.75y + 4.5z
受到四个约束:
1、这个农民有100万平方米的土地,x+y+z<=1000000
2、农民必须至少种植30万平方米的玉米和燕麦,x+y>=300000
3、由于玉米更容易受到长期干旱的影响,不希望玉米占地超过20万平方米,x<=200000
4、他想把同样的面积分配给燕麦和果园,y = z
三、真的这么简单么?
从上面的例子看,好像数学建模很简单啊。如果需要在实际工作用用到的话,需要抱着理性的态度来进行,因为上面的例子实际上就只用到小学生水平的知识,实际工作需要解决的复杂问题可能要超越大学生水平的知识。
那么大学生水平的建模问题是什么样子,我们看一个例子。
“无人机集群在遂行编队飞行时,为避免外界干扰,应尽可能保持电磁静默,少向外发射电磁波信号。为保持编队队形,拟采用纯方位无源定位的方法调整无人机的位置,即由编队中某几架无人机发射信号、其余无人机被动接收信号,从中提取出方向信息进行定位,来调整无人机的位置。编队中每架无人机均有固定编号,且在编队中与其他无人机的相对位置关系保持不变。接收信号的无人机所接收到的方向信息约定为:该无人机与任意两架发射信号无人机连线 之间的夹角(如图 1 所示)。例如:编号为 FY01、FY02 及 FY03 的无人机发射信号,编号为 FY04 的无人机接收到的方向信息是 𝛼1,𝛼2 和 𝛼3。”

请建立数学模型,解决以下问题:
问题1:编队由 10 架无人机组成,形成圆形编队,其中 9 架无人机(编号 FY01~FY09)均 匀分布在某一圆周上,另 1 架无人机(编号 FY00)位于圆心(见图 2)。无人机基于自身感知 的高度信息,均保持在同一个高度上飞行。
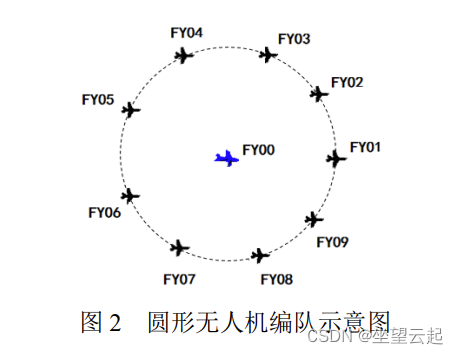
(1) 位于圆心的无人机(FY00)和编队中另 2 架无人机发射信号,其余位置略有偏差的无 人机被动接收信号。当发射信号的无人机位置无偏差且编号已知时,建立被动接收信号无人机 的定位模型。
(2) 某位置略有偏差的无人机接收到编号为 FY00 和 FY01 的无人机发射的信号,另接收到 编队中若干编号未知的无人机发射的信号。若发射信号的无人机位置无偏差,除 FY00 和 FY01 外,还需要几架无人机发射信号,才能实现无人机的有效定位?
(3) 按编队要求,1 架无人机位于圆心,另 9 架无人机均匀分布在半径为 100 m 的圆周上。 当初始时刻无人机的位置略有偏差时,请给出合理的无人机位置调整方案,即通过多次调整, 每次选择编号为 FY00 的无人机和圆周上最多 3 架无人机遂行发射信号,其余无人机根据接收 到的方向信息,调整到理想位置(每次调整的时间忽略不计),使得 9 架无人机最终均匀分布在 某个圆周上。利用表 1 给出的数据,仅根据接收到的方向信息来调整无人机的位置,请给出具 体的调整方案。
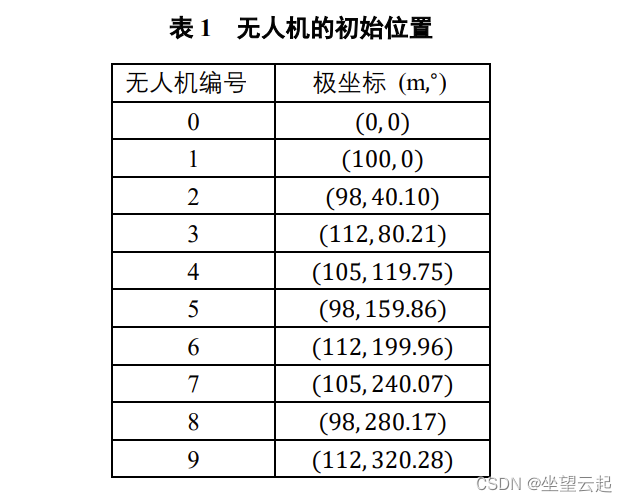
问题2:实际飞行中,无人机集群也可以是其他编队队形,例如锥形编队队形(见图 3,直 线上相邻两架无人机的间距相等,如 50 m)。仍考虑纯方位无源定位的情形,设计无人机位置 调整方案。
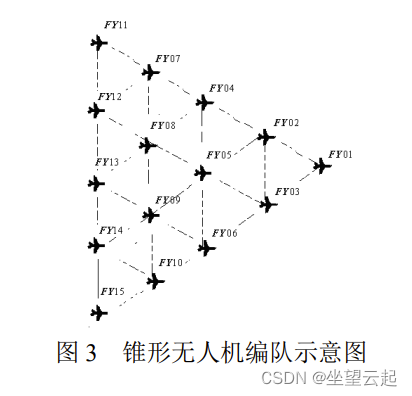
这是2022年的高教社杯全国大学生数学建模竞赛的一道赛题。如果不仔细看,光题目就很晕的感觉有没有?
所以说数学建模并不是那么简单的算术问题。
数学建模可以解决或者近似模拟现实生活中的情况,数学模型可能会变得非常复杂,因此数学规则经常被写入计算机程序,以制作计算机模型。
如果你判断未来的工作或者希望能在未来的工作中用到数学建模,值得花时间好好的学习。


![[Qt 教程之Widgets模块] —— QComboBox 组合框](https://img-blog.csdnimg.cn/6f982d13aece4db9bec20c06375533ac.png#pic_center)