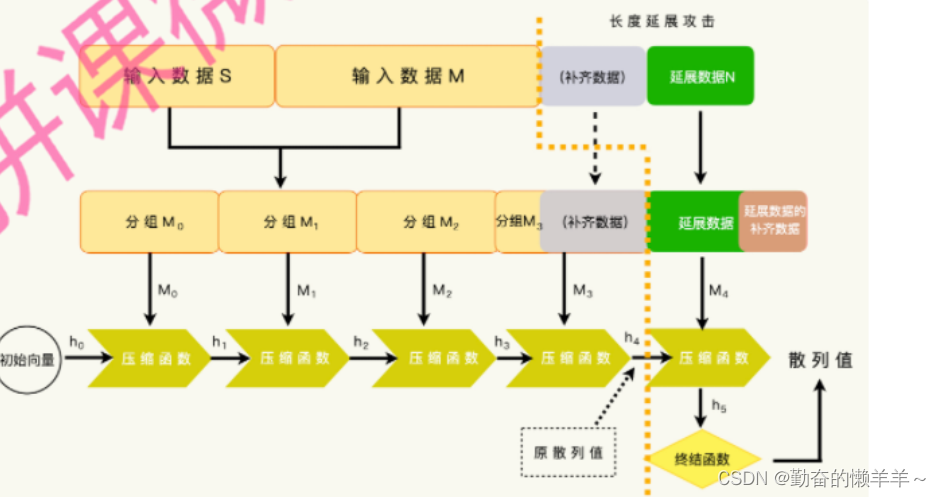
一、什么是长度延展

假设有两段数据，S和M，以及一个单向散列函数h。

如果我们要将两段数据合并起来，并且还要计算合并后的散列值，这就叫做单向散列函数的长度延展。

 二、长度延展攻击

如果S和M都是公开信息，那么S在前还是M在前是不重要的。

但如果S是机密信息，M是公开信息，S放在前面就存在“长度延展攻击”的风险。

长度延展攻击：可以利用已知数据的散列值，计算原数据外加一段延展后的散列值。

也就是说，如果我们知道了h（S|M）我们就可以计算h(S|M|N)。其中，数据N就是原数据追加的延展数据。

如果S和M都是公开的信息，那么能计算延展数据的散列值也没什么要紧的。

但如果S是机密数据，它的用途就和机密有点关系。因为没有人知道我拥有的机密数据，所以，当我给定一段公开信息M后，只有我自己能计算S和M的散列值。

通过验证S和M的散列值，就知道一个给定的散列值是我计算、派发出去的、还是别人伪造的。

机密数据放前面，就会存在“长度延展攻击”的风险，攻击者不需要知道机密数据，就可以通过一个已知的URL，构造一个新的合法的URL，也就是说，攻击者可以伪造一个合法的散列值。

攻击者如何伪造？

前面我们提到，一个单向散列函数，应该由四个部分组成：数据分组，压缩函数，链接模式，终结函数。

压缩函数接收一个数据分组和上一个压缩函数的运算结果。如果知道了上一个压缩函数的运算结果，我们就能够计算下一个分组数据的压缩函数运算结果。这里，就是出现安全漏洞的地方。

不要单纯使用单向散列函数来处理既包含机密信息、又包含公开信息的数据。即使我们把机密信息放在最后处理，这种使用方式也不省心。

如果我们需要使用机密数据产生数据的签名，我们应该使用设计好的、经过验证的算法。

另外，如果需要设计算法，我们还要理解另外一个实用的原则：算法要皮实、耐用，不能有意无意地用错了就有安全漏洞。