小朋友们好，大朋友们好！

我是猫妹，一名爱上Python编程的小学生。

和猫妹学Python，一起趣味学编程。

今日主题

咱们今天继续学习图的应用，这些算法都是实际问题抽象出来的。

举个例子吧！

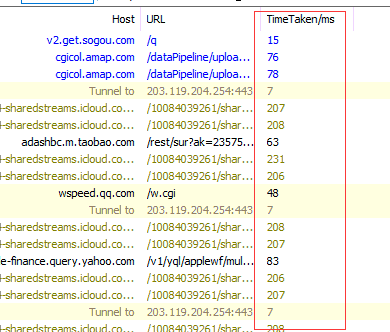
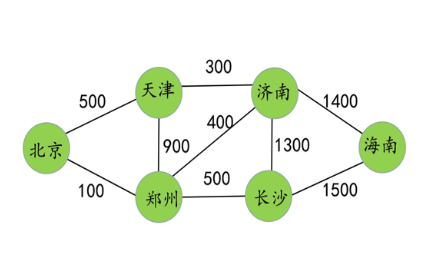
下面6个城市，不同城市之间的距离不同。

如图所示，请问如果从北京出发，到达海南，哪条路径最短？

这就需要了解下迪杰斯特拉算法(Dijkstra)了。

迪杰斯特拉算法

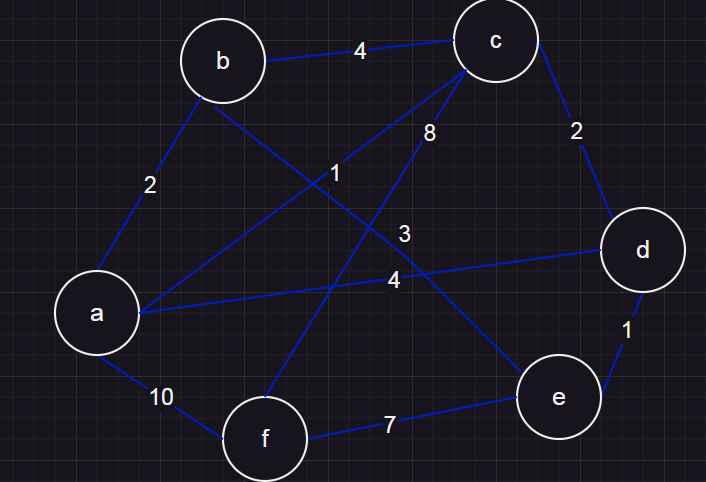
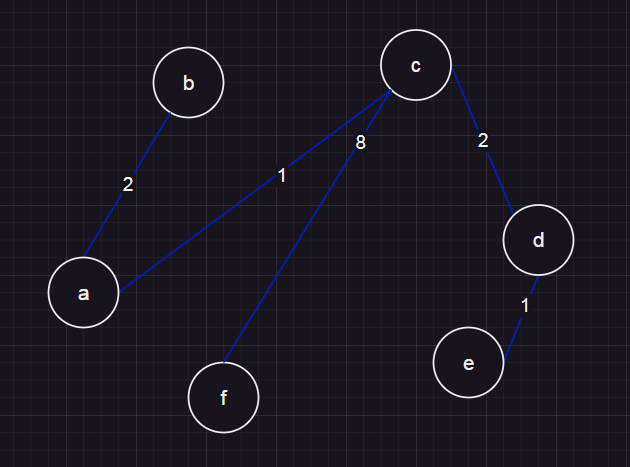
假设我们需要计算下图任意两点之间的最短距离。

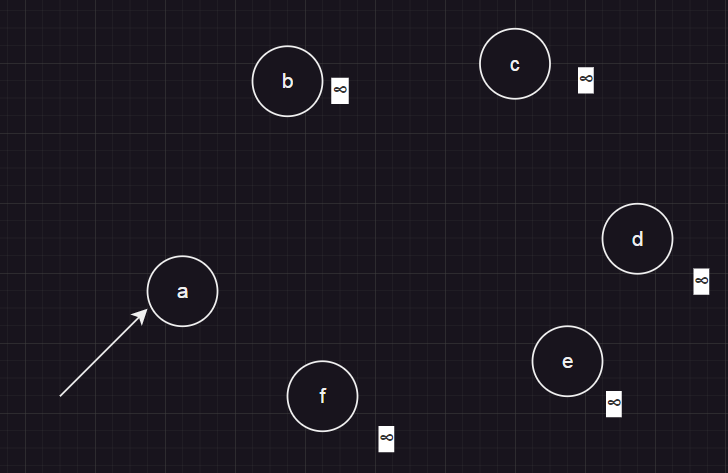
假设从a点开始，我们假设a到其他点的距离是无穷大。

第一步更新：将a起始的边，如果距离比无穷大小，更新。

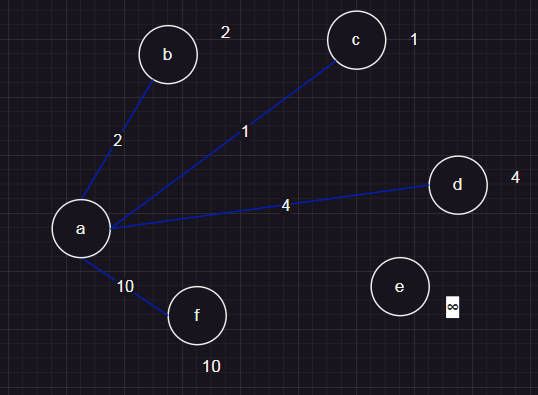
第二步更新：从a相邻的结点中，找到一个距离最近的点，也就是c点，做类似操作。

到达d点的距离1+2<4，更新4为3。

到达f点的距离1+8<10，更新10为9。

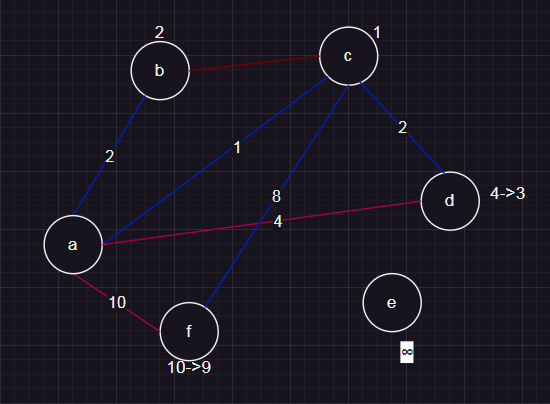
如此反复，直到所有点都被访问到。

这种算法就是迪杰斯特拉算法(Dijkstra)。

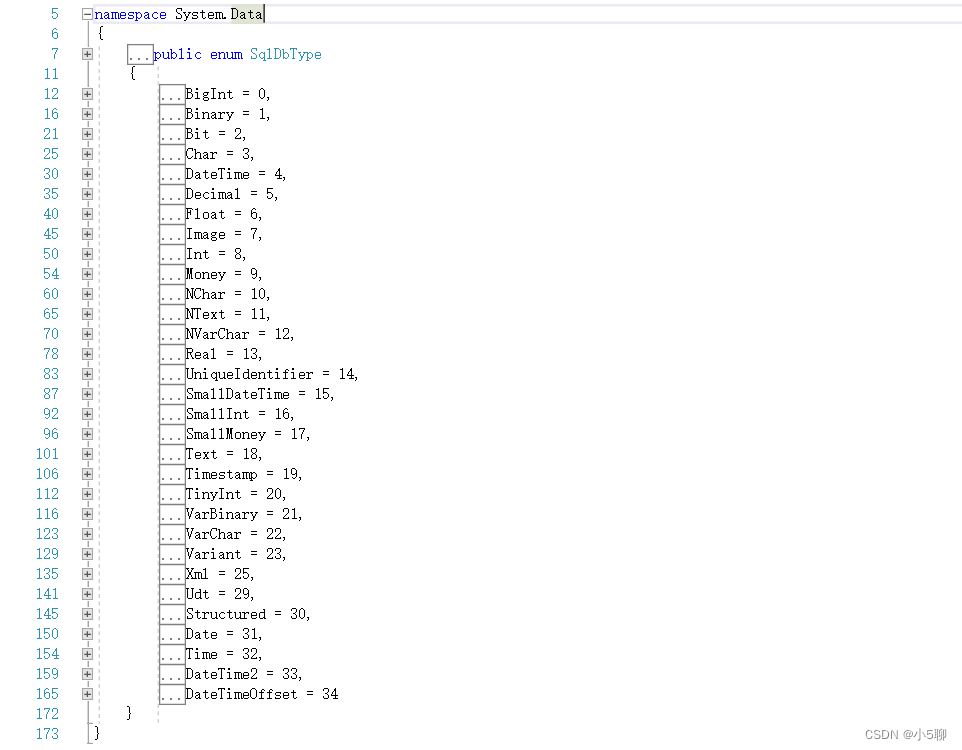
Python实现

代码实现（完整代码，见同名公众号，次条推文）：

我们用一个字典来表示图，字典中可以嵌套字典哦：

我们定义一个函数来实现核心算法：

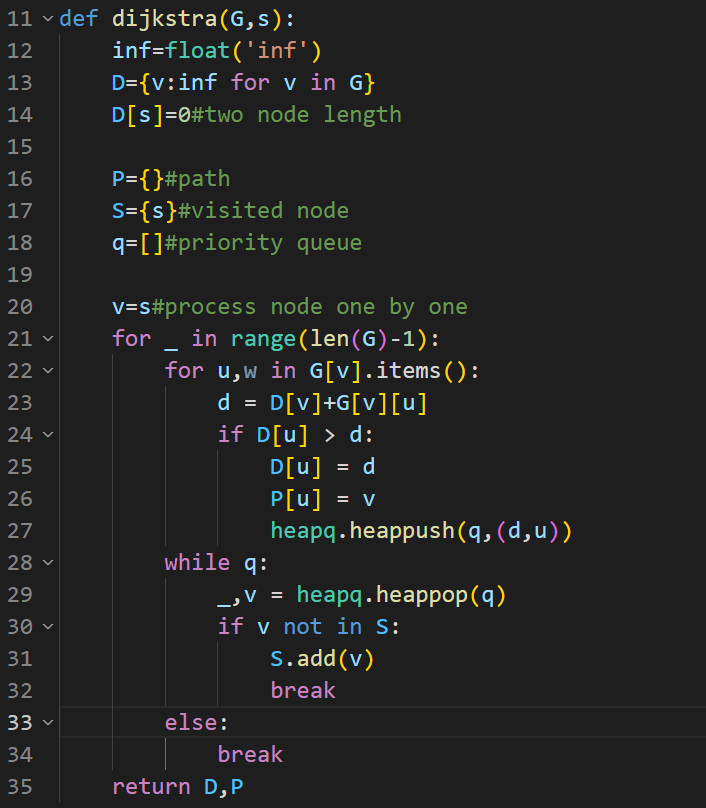
11行：G表示图，s表示起始结点

12~14行：该列表保存起始结点到本结点的距离，除了自身到自身是0外，其他都初始化为无穷大

16行：字典，路径，从起始结点到本结点的最小路径所经过的前继结点(上一个结点)

17行：集合，访问过的结点

18行：优先级队里，实现功能为，从当前结点出发的多条边中，选取最小的一个

21行：循环数为结点数减1，这里的_表示不关心循环变量

22行，从当前结点相邻的结点和边处理，一是看到相邻结点的距离是否需要更新，二是选取下一个结点

24行：如果新的路径d，比之前的路径D[u]小

25行：更新D[u]，D[u]保存的是起始结点到本结点的最小距离

26行：添加结点u的前继结点为v，也就是->v->u

27行：将距离，结点放入优先级队列。从已更新的结点中(路径当前最小)，以便选取下个结点为当前结点

28行：代码中有break，根据break退出当前循环

29行：此时v的权值和最小，最小路径，预选取它

30~32行：v没有被访问过，把它放入已访问队列

33~34行：如果有孤立结点，不和任意结点连接，会进入此分支，可先不关心这个逻辑

35行：返回D，P。D表示起始结点s到达本结点的最小距离，P表示s到达本结点的路径。

函数调用：

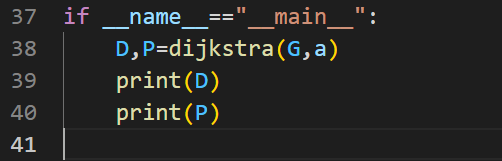
运行结果：

第一行字典中的键为结点(abcdef)，值为a到本结点最小路径。

第二行字典中的键和值都是结点。1的前继结点是0,2的前继结点是0，如此类推。

你学会了吗？

这算法真让人拍案叫绝啊！

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。

他是一名天才程序员，为计算机的发展做出了巨大的贡献。

好了，我们今天就学到这里吧！

如果遇到什么问题，咱们多多交流，共同解决。

我是猫妹，咱们下次见！