F-子串的子序列_牛客小白月赛62 (nowcoder.com)

题意：

 

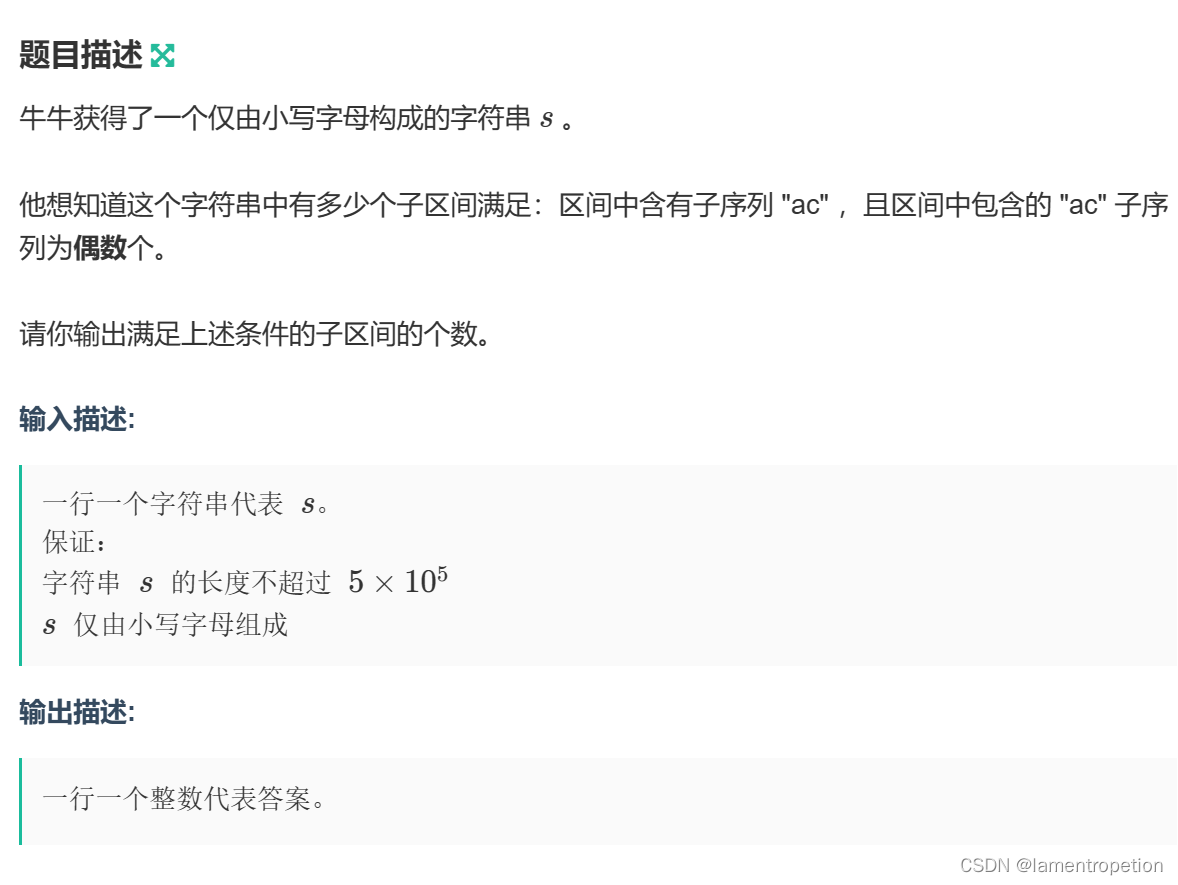
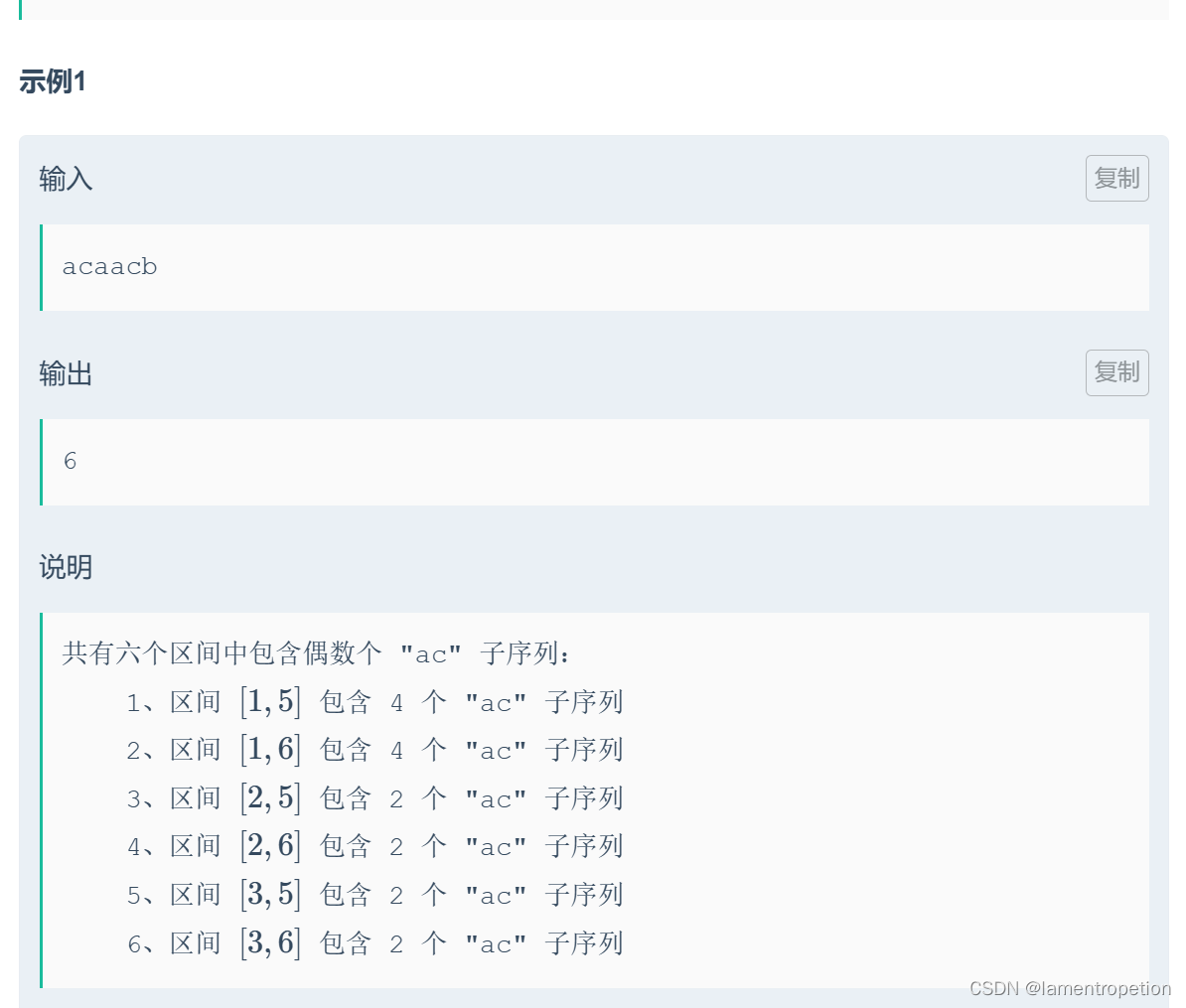
思路：

复盘一下应该有的思路：

首先n^2枚举肯定超时，我们枚举的是一个区间

枚举区间有一些trick：

1.枚举其中一个右（左）端点，O(1)或O(logn)计算满足条件的左（右）端点个数 ，可以组合数学 or DP 计算

2.单独计算每个元素的贡献，O(1)或O(logn)计算合法区间的左端点和右端点匹配个数，这种一般是乘法原理

在这里我们用到的是第一种思想

我们去枚举右端点r，然后计算满足条件的左端点的个数

我就想到这里，甚至连DP都没想到

这里的DP并不是传统意义的子序列DP，也就是说，并不是枚举两个指针然后转移(LIS)，也不是统计前缀满足某个性质的子序列的最值（接龙数列 or 绝世好题），这里用的是状态机DP

设dp[i][0/1][0/1]表示，前i个字符，a的数量的奇偶性是0/1，ac的数量的奇偶性是0/1的子串个数

为什么是这样设计的，其实一开始想的应该只是ac的数量的奇偶性，但是发现这样不能算贡献，考虑多一个字符c，贡献还与前缀a的数量的奇偶性有关，所以应该还有加上一维

这里告诉我们，在考虑计算贡献的DP时，考虑多一格，然后思考如何计算贡献

然后转移的时候注意这是子串数量，所以应该从i-1转移

（看代码）为什么一开始要++，因为考虑新加的字符自成一个区间

还有一个坑点：

然后统计答案的时候会把ac子序列个数为0的区间个数算进去，因此我们需要减去这些区间

这个怎么做？同样也是那个枚举区间的trick，我们去枚举左区间，右侧ac的c左边那格-i+1就是区间个数了，统计一下即可

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

using i64 = long long;

const int mxn=5e5+10;
const int mxe=5e5+10;
const int mod=1e9+7;

string s;

int N;
int pre_a[mxn],pre_c[mxn];
int dp[mxn][2][2];

int no_ac(){
    int res=0;
    for(int i=1;i<=N;i++){
        if(s[i]=='a'){
            pre_a[i]=i;
            pre_c[i]=pre_c[i-1];
        }else if(s[i]=='c'){
            pre_c[i]=i;
            pre_a[i]=pre_a[i-1];
        }else{
            pre_a[i]=pre_a[i-1];
            pre_c[i]=pre_c[i-1];
        }
    }
    for(int r=1;r<=N;r++) res+=r-(pre_a[pre_c[r]]+1)+1;
    return res;
}
void solve(){
    cin>>s;
    N=s.size();
    s=" "+s;
    int ans=0;
    for(int i=1;i<=N;i++){
        if(s[i]=='a'){
            dp[i][1][0]++;
            dp[i][1][1]+=dp[i-1][0][1];
            dp[i][1][0]+=dp[i-1][0][0];
            dp[i][0][1]+=dp[i-1][1][1];
            dp[i][0][0]+=dp[i-1][1][0];
        }else if(s[i]=='c'){
            dp[i][0][0]++;
            dp[i][1][1]+=dp[i-1][1][0];
            dp[i][1][0]+=dp[i-1][1][1];
            dp[i][0][1]+=dp[i-1][0][1];
            dp[i][0][0]+=dp[i-1][0][0];
        }else{
            dp[i][0][0]++;
            for(int j=0;j<2;j++){
                for(int k=0;k<2;k++){
                    dp[i][j][k]+=dp[i-1][j][k];
                }
            }
        }
        ans+=dp[i][1][0]+dp[i][0][0];
    }
    cout<<ans-no_ac()<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}