1. 回溯算法
回溯算法也叫试探法,它是一种系统地搜索问题而求解的方法。回溯算法可以找出所有解的一般性,同时可以避免不正确的数值。一旦发现不正确的数值,就不再继续下一层而是返回到上一层,以节省时间。简单来说,回溯算法就是遇到错误就退缩的一种算法。
用通俗易懂的话描述就是:通过选择不同的岔路口寻找目的地,一个岔路口、一个岔路口地去尝试找到目的地。如果走错了路,继续返回来找到岔路口的另一条路,直到找到目的地。
2. 四皇后问题
皇后是国际象棋中实力最强的棋子,可横、直、斜走,且格数不限。四皇后问题就是由此演变出来的,在4×4格的国际象棋棋盘上摆放4个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
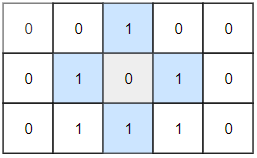
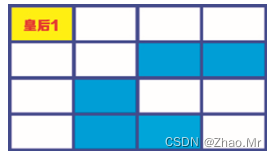
步骤1:安排皇后1的位置,皇后1是随机放的,我们这里先尝试在网格的第1个单元格放置皇后1,如图4所示。
说明:白色的单元格表示在皇后1的攻击范围内,不可以安排另一位皇后的位置,蓝色的单元格表示非皇后1的攻击范围,可以安排其他皇后的位置。
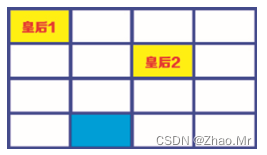
步骤2:安排皇后2的位置,皇后2可以被安排的位置有:在第2行、第3列的单元格和第2行、第4列的单元格中。下面先把皇后安排在第2行、第3列的单元格中。
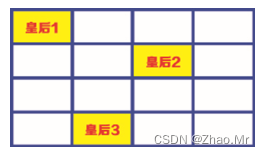
步骤3:安排皇后3的位置,此时,皇后3只能安排在第4行、第2列的单元格中。
步骤4:如果将皇后3放置在第4行第2列单元格中,此时4×4的网格全部变白(全部网格都处于已安置的皇后的攻击范围内),皇后4就没有位置安放了。此时使用回溯算法,退回到上一步,重新安排皇后3的位置。而皇后3只可以放在第4行第2列单元格中,无法更改位置,那就再退回到上一步,重新安排皇后2的位置。皇后2还可以被安排在第2行、第4列的单元格中。
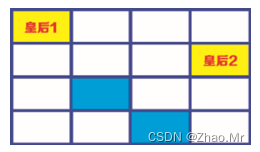
步骤5:再次安排皇后3的位置,此时皇后3只能安排在第3行、第2列的单元格中。
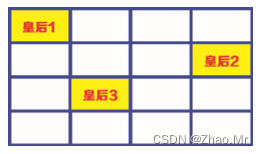
步骤6:此时4×4的网格全部变白(全部网格都处于已安置的皇后的攻击范围内),没有位置安放皇后4。使用回溯算法,退回到上一步,重新安排皇后3的位置。皇后3也无格可换,再退回到上一步重新安排皇后2的位置,而皇后2可以安排的两种可能都不可行。换句话说,皇后2也无格可换,就需要再退回到上一步,重新安排皇后1的位置,这次将皇后1的位置安排在第1行、第2列的单元格中。
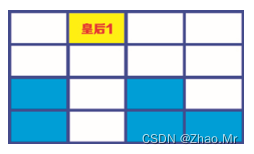
步骤7:然后安排皇后2的位置,将皇后2安排在第2行、第4列的单元格中。
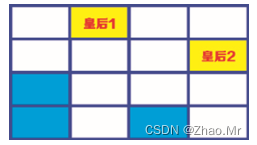
步骤8:接着安排皇后3的位置,将皇后3安排在第3行、第1列的单元格中。
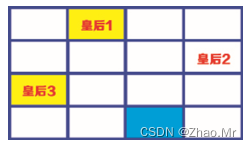
步骤9:最后安排皇后4,将皇后4安排在第4行、第3列单元格中。
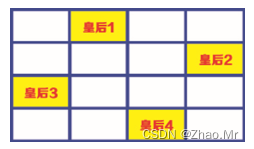
至此,已经用4×4网格将4个皇后的位置安排妥当了。